Data Anomalies

Data Anomalies

Data anomalies are inconsistencies in the data stored in a database as a result of an operation such as update, insertion, and/or deletion.

Such inconsistencies may arise when have a particular record stored in multiple locations and not all of the copies are updated.

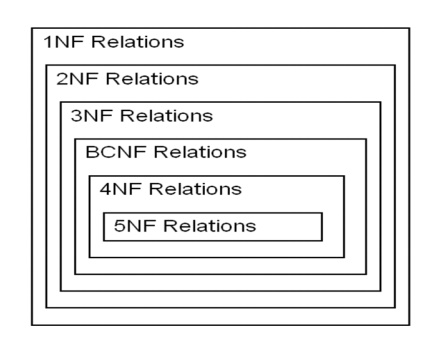
We can prevent such anomalies by implementing 7 different level of normalization called Normal Forms (NF) We’ll only look at the first three.First Normal Form (1NF)

1st Normal Form:

The Requirements:

The requirements to satisfy the 1st NF:

Each table has a primary key: minimal set of attributes which can uniquely identify a record

The values in each column of a table are atomic (No multi-value attributes allowed). There are no repeating groups: two columns do not store similar information in the same table

1st Normal Form

Example 1:

Un-normalized Students table:

Student#    AdvID        AdvName   AdvRoom  Class1         Class2

123    123A James         555    102-8 104-9

124    123B Smith         467    209-0 102-8

Normalized Students table:

Student#    AdvID        AdvName   AdvRoom  Class#

123    123A James          555    102-8

123    123A James          555    104-9

124    123B Smith          467    209-0

124    123B Smith          467    102-8

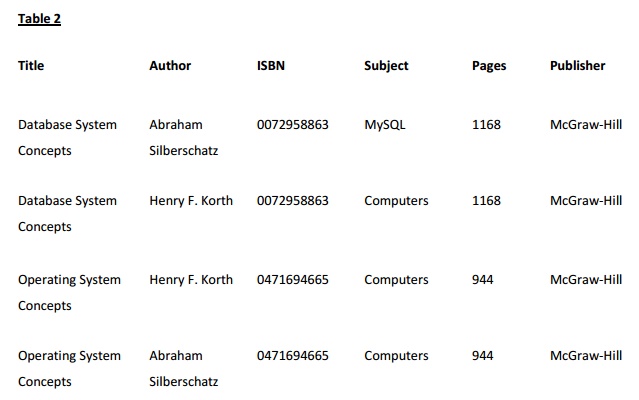
Example 2:

Title  Author1     Author2     ISBN Subject       Pages Publisher

Database     Abraham    Henry F.     0072958863         MySQL,      1168  McGraw-

System        Silberschatz          Korth                   Computers           Hill

Concepts                                                   

Operating   Abraham    Henry F.     0471694665         Computers  944    McGraw-

System        Silberschatz          Korth                                       Hill

Concepts

Table 1 problems

l        This table is not very efficient with storage.

l        This design does not protect data integrity.

l        Third, this table does not scale well.

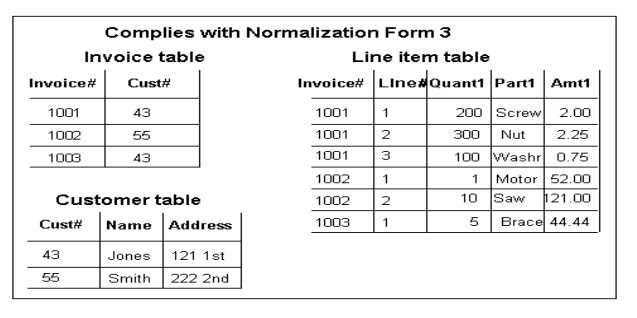
l        In our Table 1, we have two violations of First Normal Form:

l        First, we have more than one author field,

l     Second, our subject field contains more than one piece of information. With more than one value in a single field, it would be very difficult to search for all books on a given subject

l        We now have two rows for a single book. Additionally, we would be violating the Second Normal Form…

l        A better solution to our problem would be to separate the data into separate tables- an Author table and a Subject table to store our information, removing that information from the Book table:

l        Each table has a primary key, used for joining tables together when querying the data. A primary key value must be unique with in the table (no two books can have the same ISBN number), and a primary key is also an index, which speeds up data retrieval based on the primary key.

l        Now to define relationships between the tables

Relationships

Second Normal Form (2NF)

•         a form is in 2NF if and only if it is in 1NF and has no attributes which require only part of the key to uniquely identify them

•         To do - remove part-key dependencies:

1.    where a key has more than one attribute, check that each non-key attribute depends on the whole key and not part of the key

2.    for each subset of the key which determines an attribute or group of attributes create a new form. Move the dependant attributes to the new form.

3.    Add the part key to new form, making it the primary key.

4.    Mark the part key as a foreign key in the original form.

•         Result: 2NF forms

If each attribute A in a relation schema R meets one of the following criteria:

It must be in first normal form.

It is not partially dependent on a candidate key.

Every non-key attribute is fully dependent on each candidate key of the relation. Second Normal Form (or 2NF) deals with redundancy of data in vertical columns.

Example of Second Normal Form:

Here is a list of attributes in a table that is in First Normal Form:

Department

Project_Name

Employee_Name

Emp_Hire_Date

Project_Manager

Project_Name and Employee_Name are the candidate key Project_Manager are partially depend on the Employee_Name, Therefore, this table will not satisfy the Second Normal Form

In order to satisfy the Second Normal Form, we need to put the  Emp_Hire_Date and Project_Manager to other tables. We can put the Emp_Hire_Date to the Employee table and put the Project_Manager to the Project table.

 So now we have three tables:

Department                 Project

Project_Name               Project_ID

Employee_Name          Project_Name

Project_Manager

Employee

Employee_ID

Employee_Name

Employee_Hire_Date

Now, the Department table will only have the candidate key left.

Third Normal Form

A relation R is in Third Normal Form (3NF) if and only if it is:

in Second Normal Form.

Every non-key attribute is non-transitively dependent on the primary key.

An attribute C is transitively dependent on attribute A if there exists an attribute B such that A ->  B and B  -> C, then A  -> C.

Example of Third Normal Form:

Here is the Second Normal Form of the table for the invoice table:

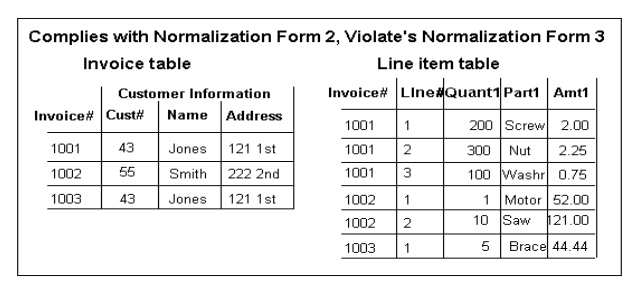
It violates the Third Normal Form because there will be redundancy for having multiple invoice number for the same customer. In this example, Jones had both invoice 1001 and 1003.

To solve the problem, we will have to have another table for the Customers

By having Customer table, there will be no transitive relationship between the invoice number and the customer name and address. Also, there will not be redundancy on the customer information

There will be more examples for the First, Second, and Third Normal Forms.

The following is the example of a table that change from each of the normal forms.

Third Normal Form:

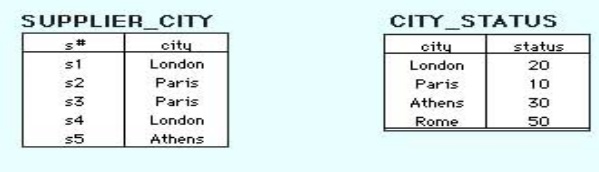
Functional Dependency of the Second Normal Form:

SUPPLIER.s# —> SUPPLIER.status (Transitive dependency)

SUPPLIER.s# —> SUPPLIER.city

SUPPLIER.city —> SUPPLIER.status

Dependency Preservation:

A FD X! Y is preserved in a relation R if R contains all the attributes of X and Y.

Why Do We Preserve The Dependency?

—        We would like to check easily that updates to the database do not result in illegal relations being created.

—        It would be nice if our design allowed us to check updates without having to compute natural joins.

Definition

 A decomposition D = {R1, R2, ..., Rn} of R is dependency-preserving with respect to F if the union of the projections of F on each Ri in D is equivalent to F; that is

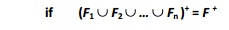
Property of Dependency-Preservation

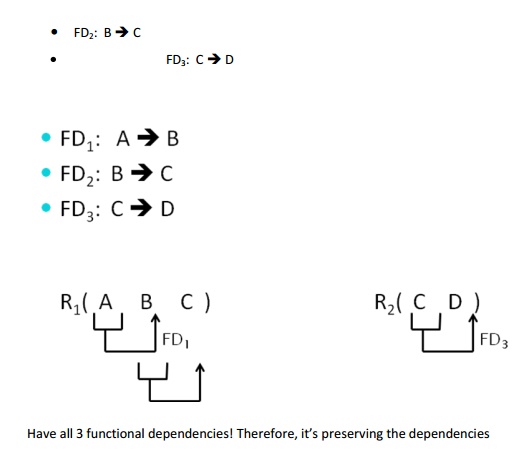
—        If decomposition is not dependency-preserving, therefore, that dependency is lost in the decomposition.

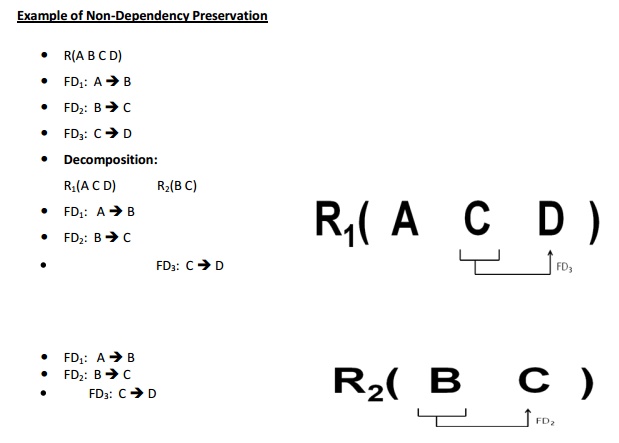
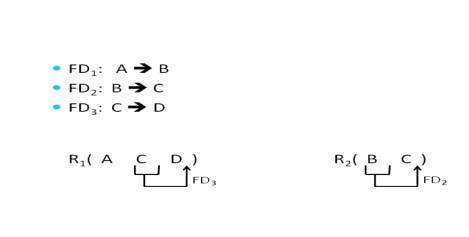
Example:

—        R(A B C D)

—        FD1: A -> B

—        FD2: B  -> C

—        FD3: C  -> D

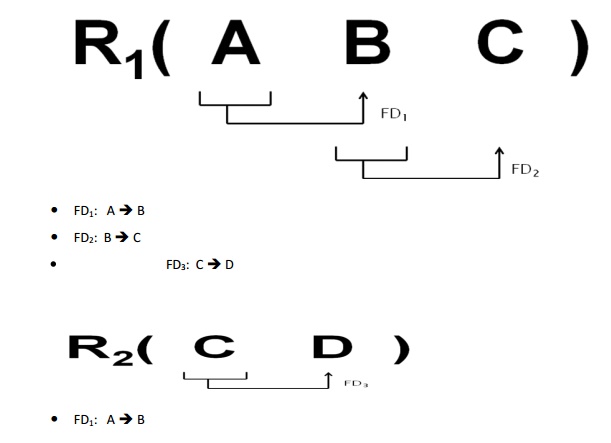
—        Decomposition:

R1(A B C)  R2(C D)

FD1: A  -> B

FD2: B  -> C

FD3: C  -> D

Boyce-Codd Normal Form:

•  A relation is in Boyce-Codd normal form (BCNF) if for every FD A   B either

•        B is contained in A (the FD is trivial), or

•        A contains a candidate key of the relation,

•         In other words: every determinant in a non-trivial dependency is a (super) key.

•         The same as 3NF except in 3NF we only worry about non-key Bs

•         If there is only one candidate key then 3NF and BCNF are the same

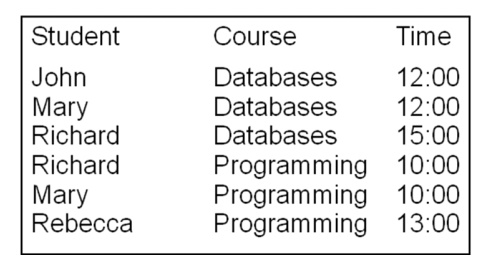
Stream and BCNF

•  Stream is not in BCNF as the FD {Time} -> {Course} is non-trivial and {Time} does not contain a candidate key

Conversion to BCNF

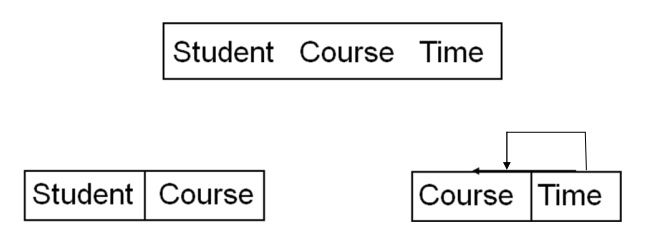
Stream has been put into BCNF but we have lost the FD {Student, Course} 

Decomposition Properties

•         Lossless: Data should not be lost or created when splitting relations up

•         Dependency preservation: It is desirable that FDs are preserved when splitting relations up

•         Normalisation to 3NF is always lossless and dependency preserving

•         Normalisation to BCNF is lossless, but may not preserve all dependencies

Higher Normal Forms:

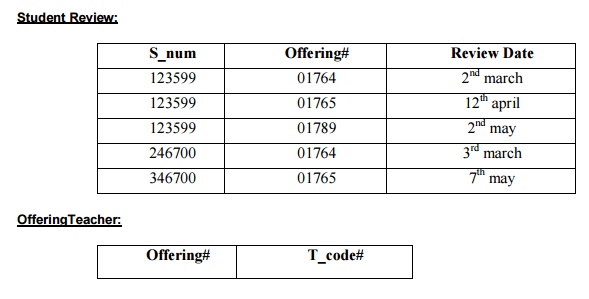
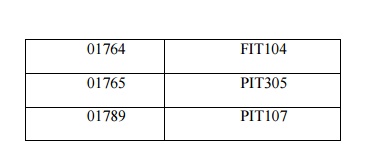
Converting to BCNF

1.    The determinant, Offering#, becomes part of the key and the dependant attribute T_Code, becomes a non key attribute. So the Dependency diagram is now

S_Num, Offering# T_Code,  Review Date

2.    There are problems with this structure as T_Code is now dependant on only part of the key. This violates the rules for 2NF, so the table needs to be divided with the partial dependency becoming a new table. The dependencies would then be

3. The original table is divided into two new tables. Each is in 3NF and in BCNF.

Note that even relations in BCNF can have anomalies.

Anomalies:

INSERT: We cannot record the city for a supplier_no without also knowing the supplier_name

DELETE: If we delete the row for a given supplier_name, we lose the information that the supplier_no is associated with a given city.

UPDATE: Since supplier_name is a candidate key (unique), there are none.

Definition of MVD

A multivalued dependency is a full constraint between two sets of attributes in a relation.

In contrast to the functional independency, the multivalued dependency requires that certain tuples be present in a relation. Therefore, a multivalued dependency is also referred as a tuple-generating dependency. The multivalued dependency also plays a role in 4NF normalization.

Full constraint

A constraint which expresses something about all attributes in a database. (In contrary to an embedded constraint.) That a multivalued dependency is a full constraint follows from its  definition, where it says something about the attributes R −  β.

Tuple-generating dependency

A dependency which explicitly requires certain tuples to be present in the relation.

A Formal Definition

Let R be a relation schema and let and . The multivalued dependency α ->> β holds on R if, in any legal relation r(R), for all pairs of tuples t1 and

Ø        A multivalued dependency on R, X ->>Y, says that if two tuples of R agree on all the attributes of X, then their components in Y may be swapped, and the result will be two tuples that are also in the relation.

i.e., for each value of X, the values of Y are independent of the values of R-X-Y

Tuples Implied by name->->phones

If we have tuples:

Example

But we cannot swap area codes or phones by themselves. That is, neither name->->areaCode nor name->->phone holds for this relation.

Properties of MVD

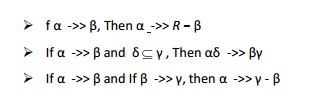
The following also involve functional dependencies:

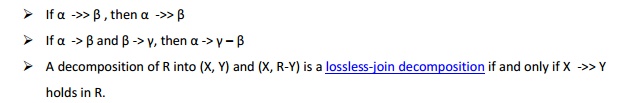
MVD Rules

•  Every  FD  is  an  MVD

– If X ‐>Y, then swapping Y ’s between two tuples that agree on X doesn’t change the tuples.

– Therefore, the “new” tuples are surely in the relation, and we know X ‐>‐>Y.

• Definition of keys depend on FDs and not MDs.

n        Requires that other tuples of a certain form be present in the relation.

n        Also referred to as:

“Tuple-generating dependency”

We can use multivalued dependencies

n        To test relations to determine whether they are legal under a given set of functional and multivalued dependencies

n        To specify constraints on the set of legal relations.

4th Normal Form

A Boyce Codd normal form relation is in fourth normal form if

Ø        there is no multi value dependency in the relation or

Ø        there are multi value dependency but the attributes, which are multi value dependent on a specific attribute, are dependent between themselves.

Ø        This is best discussed through mathematical notation.

Ø        Assume the following relation

(a) R(a:pk1, b:pk2, c:pk3)

Ø        Recall that a relation is in BCNF if all its determinant are candidate keys, in other words each determinant can be used as a primary key.

Ø     Because relation R has only one determinant (a, b, c), which is the composite primary key and since the primary is a candidate key therefore R is in BCNF.

Now R may or may not be in fourth normal form.

Ø        If R contains no multi value dependency then R will be in Fourth normal form.

Ø        Assume R has the following two-multi value dependencies:

 a --->> b and a --->> c

In this case R will be in the fourth normal form if b and c dependent on each other.

Ø        However if b and c are independent of each other then R is not in fourth normal form and the relation has to be projected to following two non-loss projections. These non-loss projections will be in fourth normal form.

Many-to-many relationships

Ø        Fourth Normal Form applies to situations involving many-to-many relationships.

Ø        In relational databases, many-to-many relationships are expressed through cross-reference tables.

Note about FDs and MVDs

Every Functional Dependency is a MVD 

(if A1A2…An ® B1B2…Bn , then A1A2…An Þ B1B2…Bn ) 

Ø        FDs rule out certain tuples (i.e. if A ® B then two tuples will not have the same value for A and different values for B)

Ø     MVDs do not rule out tuples. They guarantee that certain tuples must exist

4th NF and Anomalies

n        As an example of the anomalies that can occur, realize that it is not possible to add a new class taught by some teacher without adding at least one student who is enrolled in this class.

n        To achieve 4NF, represent each independent many-to-many relationship through its own cross-reference table.

Case 1:

Assume the following relation:

Employee (Eid:pk1, Language:pk2, Skill:pk3)

No multi value dependency, therefore R is in fourth normal form.

Case 2:

Assume the following relation with multi-value dependency:

Employee (Eid:pk1, Languages:pk2, Skills:pk3)

Eid --->> Languages    Eid --->> Skills

Languages and Skills are dependent.

This says an employee speak several languages and has several skills. However for each skill a specific language is used when that skill is practiced

Thus employee 100 when he/she teaches speaks English but when he cooks speaks French. This relation is in fourth normal form and does not suffer from any anomalies.

Case 3:

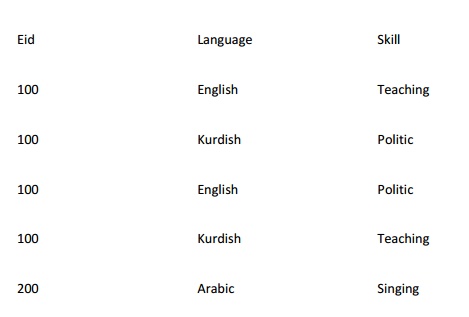
Assume the following relation with multi-value dependency:

Employee (Eid:pk1, Languages:pk2, Skills:pk3)

Eid --->> Languages   Eid --->> Skills

Languages and Skills are independent.

This relation is not in fourth normal form and suffers from all three types of anomalies

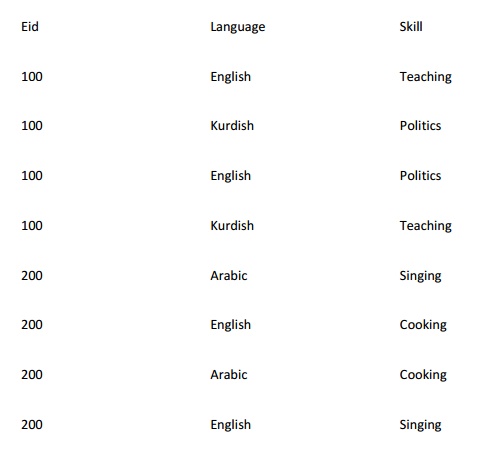
Insertion anomaly: To insert row (200 English Cooking) we have to insert two extra rows (200 Arabic cooking), and (200 English Singing) otherwise the database will be inconsistent. Note the table will be as follow:

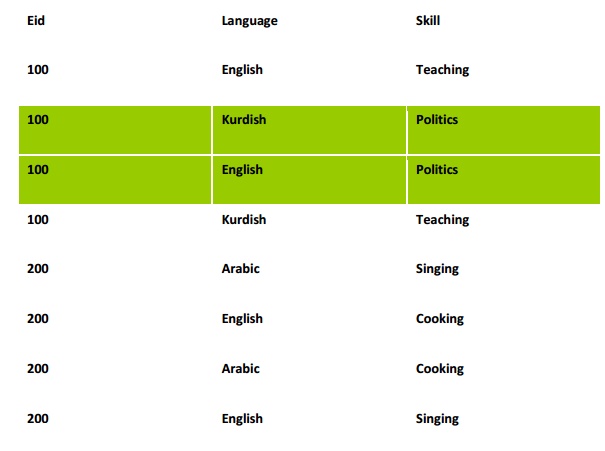
Deletion anomaly: If employee 100 discontinues politic skill we have to delete two rows:  (100 Kurdish Politic), and (100 English Politic) otherwise the database will be inconsistent.

FIFTH NORMAL FORM

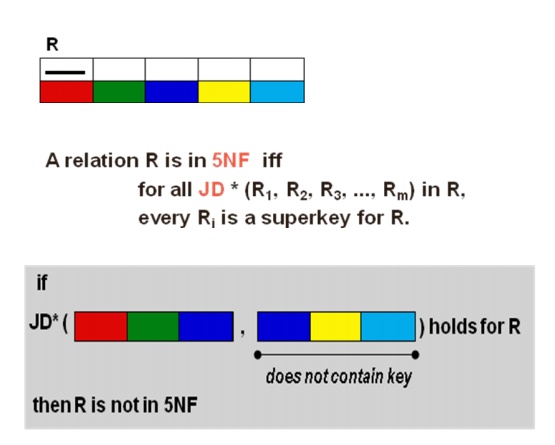
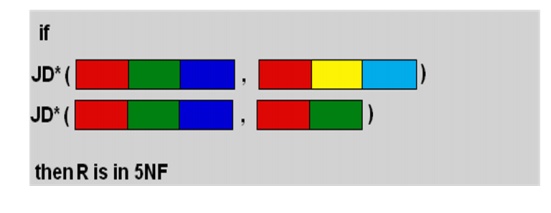
R is in 5NF if and only if every join dependency in R is implied by the candidate keys of R

w       5NF is always achievable.

w    a join dependency, * (A, B, …, Z), is implied by the candidate keys, K1, …, Km of R

w     the fact that K1, …, Km are candidate keys for R determine the fact that R has the JD * (A, B, …, Z)

Problems in bringing a relation to 5NF

w        check whether all JDs are implied by the candidate keys

§       Fagin : provides an algorithm for doing this for any relation, given all its JDs and all candidate keys

w        discover all JDs for a given relation

§       they do not have that intuitive meaning as FDs or MVDs

w        A relation is in 5NF if every join dependency in the relation is implied by the keys of the relation

w        Implies that relations that have been decomposed in previous normal forms can be recombined via natural joins to recreate the original relation.

Usage

Only in rare situations does a 4NF table not conform to 5NF. These are situations in which a complex real-world constraint governing the valid combinations of attribute values in the 4NF table is not implicit in the structure of that table. If such a table is not normalized to 5NF, the burden of maintaining the logical consistency of the data within the table must be carried partly by the application responsible for insertions, deletions, and updates to it; and there is a heightened risk that the data within the table will become inconsistent. In contrast, the 5NF design excludes the possibility of such inconsistencies.

Example 2:

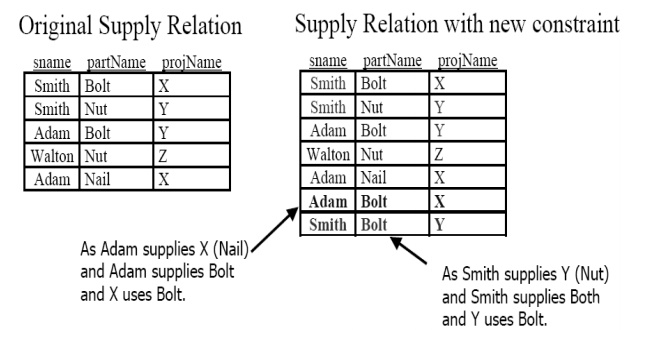
Consider a relation Supply (sname, partName, projName). Add the additional constraint that:

If project j requires part p

and supplier s supplies part p

and supplier s supplies at least one item to project j Then

supplier s also supplies part p to project

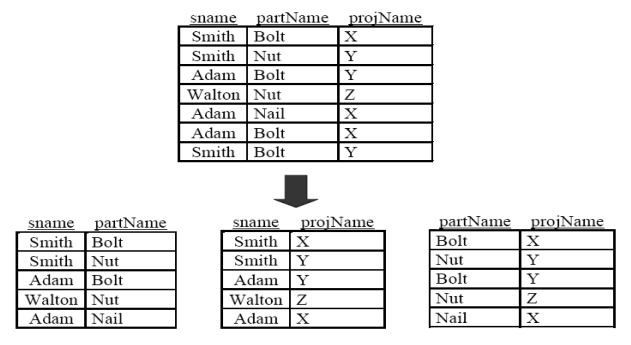
Let R be in BCNF and let R have no composite keys. Then R is in 5NF

Note: That only joining all three relations together will get you back to the original relation. Joining any two will create spurious tuples!