Buffers

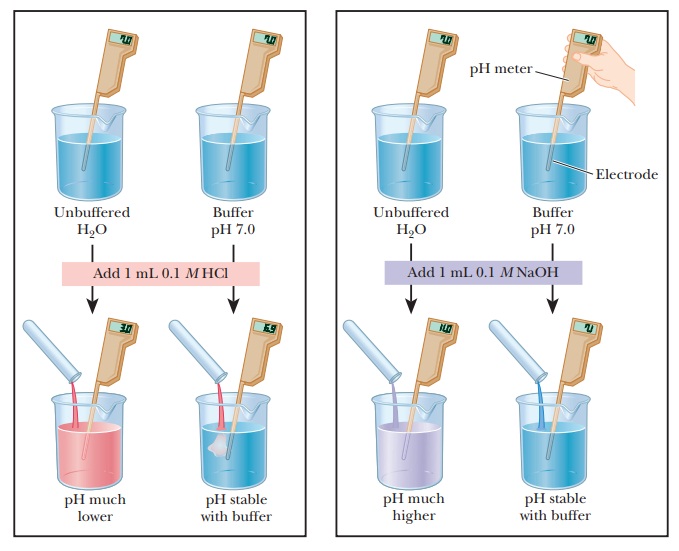
Buffers

A buffer is something that resists change. In terms of acid and base chemistry, a buffer solution tends to resist change in pH when small to moderate amounts of a strong acid or strong base are added. A buffer solution consists of a mixture of a weak acid and its conjugate base.

How do buffers work?

Let us compare the changes in pH that occur on the addition of equal amounts of strong acid or strong base to pure water at pH 7 and to a buffer solution at pH 7. If 1.0 mL of 0.1 M HCl is added to 99.0 mL of pure water, the pH drops drastically. If the same experiment is conducted with 0.1 M NaOH instead of 0.1 M HCl, the pH rises drastically (Figure 2.14).

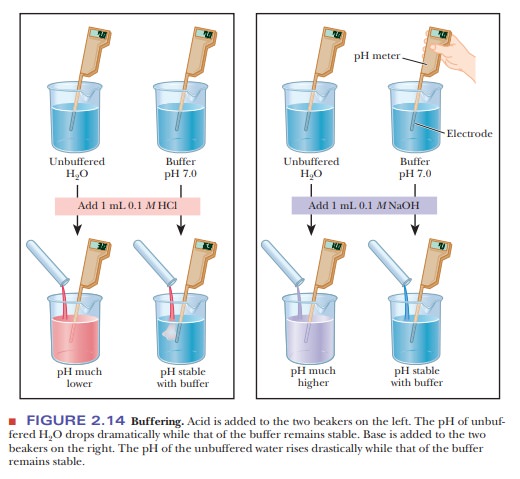
The results are different when 99.0 mL of buffer solution is used instead of pure water. A solution that contains the monohydrogen phosphate and dihydrogen phosphate ions, HPO₄^2- and H₂PO₄^-, in suitable proportions can serve as such a buffer. The Henderson–Hasselbalch equation can be used to calculate the HPO₄^2-/H₂PO₄^- ratio that corresponds to pH 7.0.

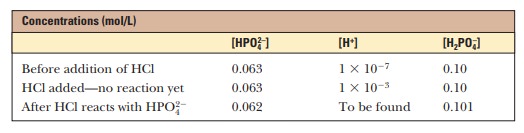
For purposes of illustration, let us consider a solution in which the concen-trations are [HPO₄^2-] = 0.063 M and [H₂PO₄^-] = 0.10 M; this gives the conjugate base/weak acid ratio of 0.63 seen previously. If 1.0 mL of 0.10 M HCl is added to 99.0 mL of the buffer, the reaction

[HPO₄^2-] 1 H⁺ ßà H₂PO₄^-

takes place, and almost all the added H⁺ will be used up. The concentrations of [HPO₄^2-] and [H₂PO₄^-] will change, and the new concentrations can be calculated.

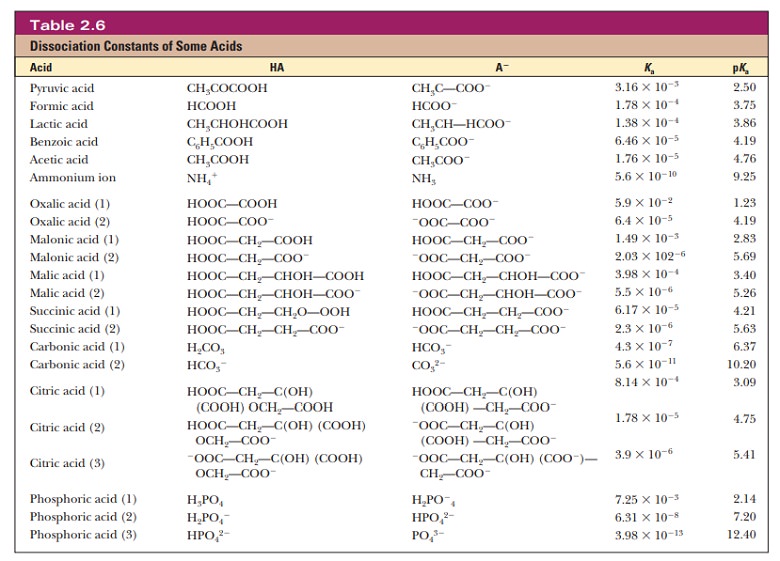
The new pH can then be calculated using the Henderson-Hasselbalch equation and the phosphate ion concentrations. The appropriate pK_a is 7.20 (Table 2.6).

The new pH is 6.99, a much smaller change than in the unbuffered pure water (Figure 2.14). Similarly, if 1.0 mL of 0.1 M NaOH is used, the same reaction takes place as in a titration:

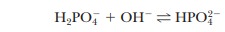
Almost all the added OH^- is used up, but a small amount remains. Because this buffer is an aqueous solution, it is still true that K_w= [H⁺][OH^-]. The increase in hydroxide ion concentration implies that the hydrogen ion concentration decreases and that the pH increases. Use the Henderson–Hasselbalch equation to calculate the new pH and to convince yourself that the result is pH 5 7.01, again a much smaller change in pH than took place in pure water (Figure 2.14). Many biological reactions will not take place unless the pH remains within fairly narrow limits, and, as a result, buffers have great practical importance in the biochemistry laboratory.

How do we choose a buffer?

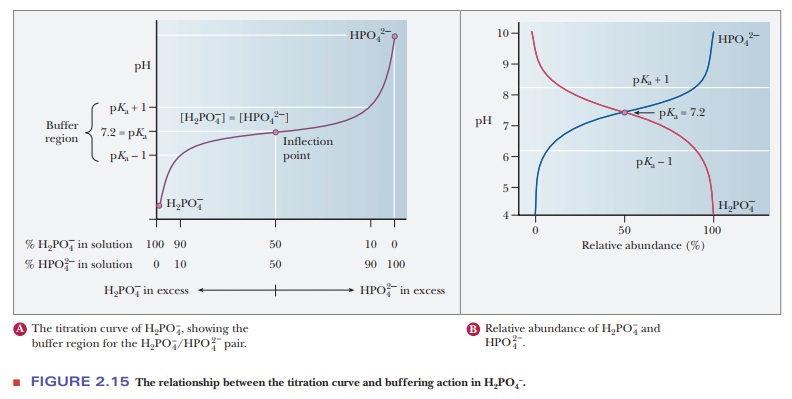
A consideration of titration curves can give insight into how buffers work (Figure 2.15a). The pH of a sample being titrated changes very little in the vicinity of the inflection point of a titration curve. Also, at the inflection point, half the amount of acid originally present has been converted to the conjugate base. The second stage of ionization of phosphoric acid,

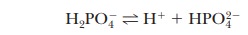
was the basis of the buffer just used as an example. The pH at the inflection point of the titration is 7.20, a value numerically equal to the pK_a of the dihydrogen phosphate ion. At this pH, the solution contains equal concentrations of the dihydrogen phosphate ions and monohydrogen phosphate ions, the acid and base forms. Using the Henderson–Hasselbalch equation, we can calculate the ratio of the conjugate base form to the conjugate acid form for any pH when we know the pK_a. For example, if we choose a pH of 8.2 for a buffer composed of H₂PO₄^- and HPO₄^2-, we can solve for the ratio

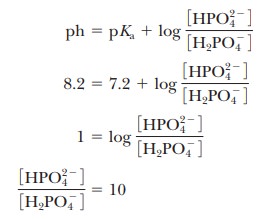
Thus, when the pH is one unit higher than the pK_a, the ratio of the conjugate base form to the conjugate acid form is 10. When the pH is two units higher than the pK_a, the ratio is 100, and so on. Table 2.7 shows this relationship for several increments of pH value.

A buffer solution can maintain the pH at a relatively constant value because of the presence of appreciable amounts of both the acid and its conjugate base. This condition is met at pH values at or near the pK_a of the acid. If OH⁺ is added, an appreciable amount of the acid form of the buffer is present in solu-tion to react with the added base. If H⁺ is added, an appreciable amount of the basic form of the buffer also is present to react with the added acid.

The H₂PO₄/HPO₄^- pair is suitable as a buffer near pH 7.2, and the CH₃COOH/CH₃COO^- pair is suitable as a buffer near pH 4.76. At pH values below the pK_a, the acid form predominates, and at pH values above the pK_a, the basic form predominates. The plateau region in a titration curve, where the pH does not change rapidly, covers a pH range extending approximately one pH unit on each side of the pK_a. Thus, the buffer is effective within a range of about two pH units (Figure 2.15b).

In many biochemical studies, a strict pH range must be maintained in order for the experiment to be successful. Using our knowledge of the range of an effective buffer compared to its pK_a, we can select an appropriate buffer. If we were doing an experiment and needed the pH to be 7.2, we might select the H₂PO₄/HPO₄^- pair to be our buffer. If we wanted a pH near 9.0, we would look at tables of buffers to find one with a pK_a close to nine. The following Biochemical Connections box goes into greater detail on buffer selection.

The condition that a buffer contains appreciable amounts of both a weak acid and its conjugate base applies both to the ratio of the two forms and to the absolute amount of each present in a given solution. If a buffer solution contained a suitable ratio of acid to base, but very low concentrations of both, it would take very little added acid to use up all of the base form, and vice versa. A buffer solution with low concentrations of both the acid and base forms is said to have a low buffering capacity. A buffer that contains greater amounts of both acid and base has a higher buffering capacity.

How do we make buffers in the laboratory?

When we study buffers in theory, we often use the Henderson2Hasselbalch equation and do many calculations concerning ratios of conjugate base form to conjugate acid form. In practice, however, making a buffer is much easier. To have a buffer, all that is necessary are the two forms of the buffer present in the solution at reasonable quantities. 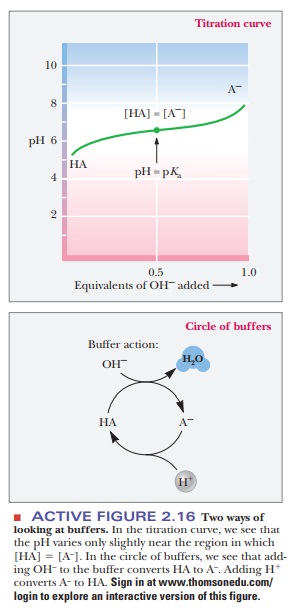This situation can be obtained by adding predetermined amounts of the conjugate base form (A^-) to the acid form (HA), or we could start with one and create the other, which is how it is usually done in practice. Remember that HA and A^- are interconverted by adding strong acid or strong base (Figure 2.16). To make a buffer, we could start with the HA form and add NaOH until the pH is correct, as determined by a pH meter. We could also start with A^- and add HCl until the pH is correct. Depending on the relationship of the pH we desire to the pK_a of the buffer, it may be more convenient to start with one than the other. For example, if we are making an acetic acid/acetate buffer at pH 5.7, it would make more sense to start with the A^- form and to add a small amount of HCl to bring the pH down to 5.7, rather than to start with HA and to add much more NaOH to bring the pH up past the pK_a.

Are naturally occurring pH buffers present in living organisms?

Up until now, we have been considering buffers from the perspective of a chemist trying to control an experiment. However, the real importance of buffers is that they are critical to life. Buffer systems in living organisms and in the laboratory are based on many types of compounds. Because physiological pH in most organisms stays around 7, it might be expected that the phosphate buffer system would be widely used in living organisms. This is the case where phosphate ion concentrations are high enough for the buffer to be effective, as in most intracellular fluids.

The H₂PO₄/HPO₄^- pair is the principal buffer in cells. In blood, phosphate ion levels are inadequate for buffering, and a different system operates.

The buffering system in blood is based on the dissociation of carbonic acid (H₂CO₃):

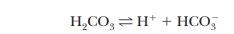
where the pK_a of H₂CO₃ is 6.37. The pH of human blood, 7.4, is near the end of the buffering range of this system, but another factor enters into the situation.

Carbon dioxide can dissolve in water and in water-based fluids, such as blood. The dissolved carbon dioxide forms carbonic acid, which, in turn, reacts to produce bicarbonate ion:

At the pH of blood, which is about one unit higher than the pK_a of carbonic acid, most of the dissolved CO₂ is present as HCO₃^-. The CO₂ being transported to the lungs to be expired takes the form of bicarbonate ion. A direct relationship exists between the pH of the blood and the pressure of carbon dioxide gas in the lungs. The properties of hemoglobin, the oxygen-carrying protein in the blood, also enter into the situation.

The phosphate buffer system is common in the laboratory (in vitro, outside the living body) as well as in living organisms (in vivo). The buffer system based on TRIS [tris(hydroxymethyl)aminomethane] is also widely used in vitro. Other buffers that have come into wide use more recently are zwitterions, which are compounds that have both a positive charge and a negative charge. Zwitterions are usually considered less likely to interfere with biochemical reactions than some of the earlier buffers (Table 2.8).

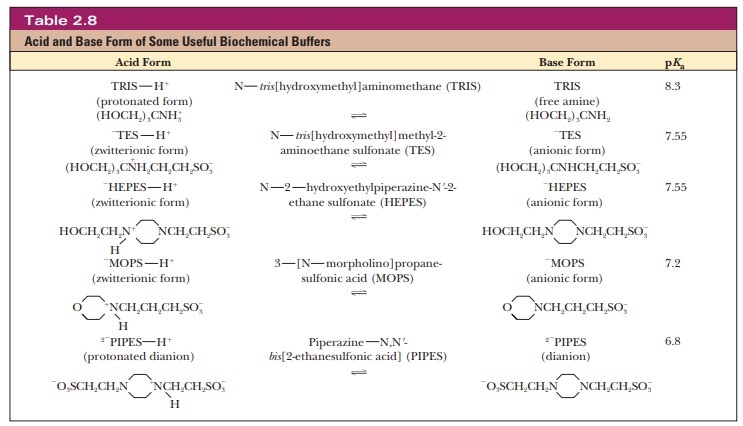
Most living systems operate at pH levels close to 7. The pK_a values of many functional groups, such as the carboxyl and amino groups, are well above or well below this value. As a result, under physiological conditions, many important biomolecules exist as charged species to one extent or another. The practical

Summary

Buffer solutions are characterized by their tendency to resist pH change when small amounts of strong acid or strong base are added.

Buffers work because the concentration of the weak acid and base is kept in the narrow window of the acid titration curve.

Many experiments must have a buffered system to keep a stable pH.

Many physiological buffers, such as the bicarbonate blood buffer or the phosphate buffer, help maintain physiological pH.