Acids, Bases, and pH

Acids, Bases, and pH

The biochemical behavior of many important compounds depends on their acid–base properties.

What are acids and bases?

A biologically useful definition of an acid is a molecule that acts as a proton (hydrogen ion) donor. A base is similarly defined as a proton acceptor. How readily acids or bases lose or gain protons depends on the chemical nature of the compounds under consideration. The degree of dissociation of acids in water, for example, ranges from essentially complete dissociation for a strong acid to practi-cally no dissociation for a very weak acid, and any intermediate value is possible.

It is useful to derive a numerical measure of acid strength, which is the amount of hydrogen ion released when a given amount of acid is dissolved in water. Such an expression, called the acid dissociation constant, or K_a, can be written for any acid, HA, that reacts according to the equation

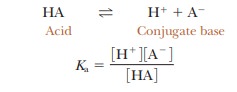
In this expression, the square brackets refer to molar concentration-that is, the concentration in moles per liter. For each acid, the quantity K_a has a fixed numerical value at a given temperature. This value is larger for more completely dissociated acids; thus the greater the K_a, the stronger the acid.

Strictly speaking, the preceding acid–base reaction is a proton-transfer reac-tion in which water acts as a base as well as the solvent. A more correct way to write the equation is as follows:

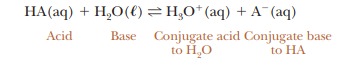
The notation (aq) refers to solutes in aqueous solution, whereas ( ) refers to water in the liquid state. It is well established that there are no “naked protons” (free hydrogen ions) in solution; even the hydronium ion (H₃O¹) is an underestimate of the degree of hydration of hydrogen ion in aqueous solution. All solutes are extensively hydrated in aqueous solution. We will write the short form of equations for acid dissociation in the interest of simplicity, but the role of water should be kept in mind throughout our discussion.

What is pH?

The acid–base properties of water play an important part in biological processes because of the central role of water as a solvent. The extent of self-dissociation of water to hydrogen ion and hydroxide ion,

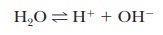
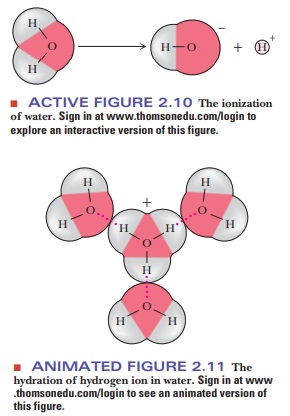
is small, but the fact that it takes place determines important properties of many solutes (Figure 2.10). Both the hydrogen ion (H⁺) and the hydroxide ion (OH^-) are associated with several water molecules, as are all ions in aqueous solution, and the water molecule in the equation is itself part of a cluster of such molecules (Figure 2.11). It is especially important to have a quantitative estimate of the degree of dissociation of water. We can start with the expression

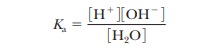
The molar concentration of pure water, [H₂O], is quite large compared to any possible concentrations of solutes and can be considered a constant. (The numerical value is 55.5 M, which can be obtained by dividing the number of grams of water in 1 L, 1000 g, by the molecular weight of water, 18 g/mol; 1000/18 5 55.5 M.) Thus,

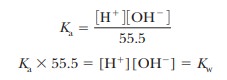
A new constant, K_w, the ion product constant for water, has just been defined, where the concentration of water has been included in its value.

The numerical value of K_w can be determined experimentally by measuring the hydrogen ion concentration of pure water. The hydrogen ion concentra-tion is also equal, by definition, to the hydroxide ion concentration because water is a monoprotic acid (one that releases a single proton per molecule). At 25°C in pure water,

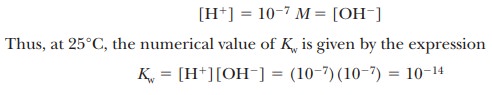
This relationship, which we have derived for pure water, is valid for any aqueous solution, whether neutral, acidic, or basic.

The wide range of possible hydrogen ion and hydroxide ion concentrations in aqueous solution makes it desirable to define a quantity for expressing these concentrations more conveniently than by exponential notation. This quantity is called pH and is defined as

with the logarithm taken to the base 10. Note that, because of the logarithms involved, a difference of one pH unit implies a tenfold difference in hydrogen ion concentration, [H⁺]. The pH values of some typical aqueous samples can be determined by a simple calculation.

When a solution has a pH of 7, it is said to be neutral, like pure water. Acidic solutions have pH values lower than 7, and basic solutions have pH values higher than 7.

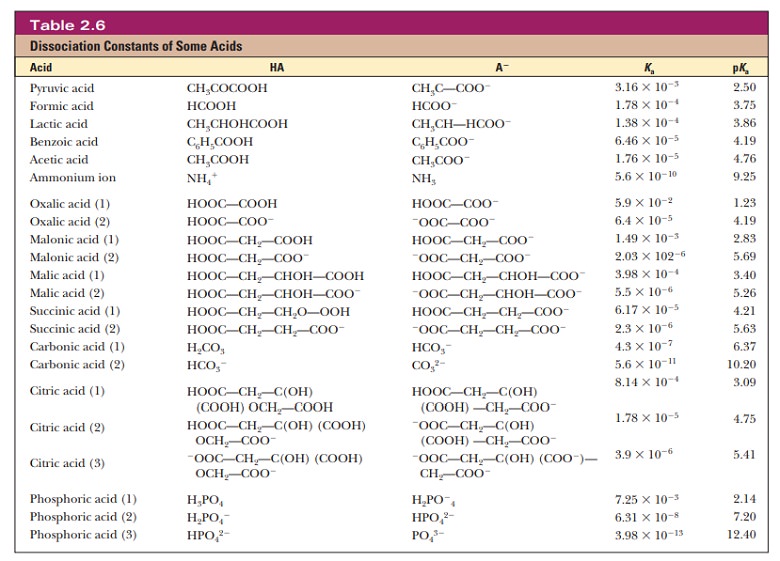
In biochemistry, most of the acids encountered are weak acids. These have a K_awell below 1. To avoid having to use numbers with large, negative exponents,a similar quantity, pK_a, has been defined by analogy with the definition of pH:

pK_a= -log₁₀K_a

The pK_a is a more convenient numerical measure of acid strength. The smaller its value, the stronger the acid. This is the reverse of the situation with K_a, where larger values imply stronger acids (Table 2.6).

Why do we want to know the pH?

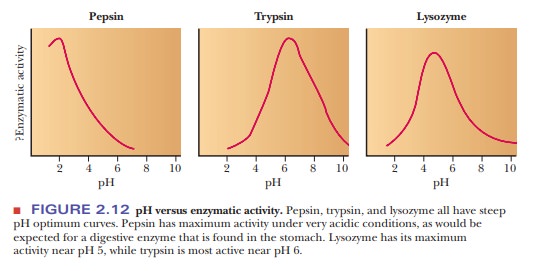
An equation connects the K_a of any weak acid with the pH of a solution containing both that acid and its conjugate base. This relationship has wide use in biochemistry, especially where it is necessary to control pH for optimum reaction conditions. Some reactions cannot take place if the pH varies from the optimum value. Important biological macromolecules lose activity at extremes of pH. Figure 2.12 shows how the activities of three enzymes are affected by pH. Note that each one has a peak activity that falls off rapidly as the pH is changed from the optimum. Also, some drastic physiological consequences can result from pH fluctuations in the body. To derive the involved equation, it is first necessary to take the logarithm of both sides of the K_a equation.

This relationship is known as the Henderson–Hasselbalch equation and is useful in predicting the properties of buffer solutions used to control the pH of reaction mixtures. 

When buffers are discussed, we will be interested in the situation in which the concentration of acid, [HA], and the concentration of the conjugate base, [A^-], are equal ([HA] = [A^-]). The ratio [A^-]/[HA] is then equal to 1, and the logarithm of 1 is equal to zero. Therefore, when a solution contains equal concentrations of a weak acid and its conjugate base, the pH of that solution equals the pK_a value of the weak acid.

Summary

Acids are proton donors, and bases are proton acceptors.

Water can accept or donate protons.

The strength of an acid is measured by its acid dissociation constant, K_a. The larger the K_a, the stronger the acid and the more H⁺ dissociates.

The concentration of H⁺ is expressed conveniently as the pH, which is the negative log of the hydrogen ion concentration.

A similar expression, pK_a, can be used in place of the K_a. pK_a5 2log K_a.

The pH of a solution of a weak acid and its conjugate base is related to the concentration of the acid and base and the pK_a by the Henderson–Hasselbalch equation.