Boolean Algebra and Logic Gates

BOOLEAN ALGEBRA AND MINIMIZATION

1 Introduction:

The English mathematician George Boole (1815-1864) sought to give symbolic form to Aristotle‘s system of logic. Boole wrote a treatise on the subject in 1854, titled An Investigation of the Laws of Thought, on Which Are Founded the Mathematical Theories of Logic and Probabilities, which codified several rules of relationship between mathematical quantities limited to one of two possible values: true or false, 1 or 0. His mathematical system became known as Boolean algebra.

All arithmetic operations performed with Boolean quantities have but one of two possible Outcomes: either 1 or 0. There is no such thing as .2. or .-1. or .1/2. in the Boolean world. It is a world in which all other possibilities are invalid by fiat. As one might guess, this is not the kind of math you want to use when balancing a checkbook or calculating current through a resistor.

However, Claude Shannon of MIT fame recognized how Boolean algebra could be applied to on-and-off circuits, where all signals are characterized as either .high. (1) or .low. (0). His1938 thesis, titled A Symbolic Analysis of Relay and Switching Circuits, put Boole‘s theoretical work to use in a way Boole never could have imagined, giving us a powerful mathematical tool for designing and analyzing digital circuits.

Like .normal. algebra, Boolean algebra uses alphabetical letters to denote variables. Unlike .normal. algebra, though, Boolean variables are always CAPITAL letters, never lowercase.

Because they are allowed to possess only one of two possible values, either 1 or 0, each and every variable has a complement: the opposite of its value. For example, if variable .A. has a value of 0, then the complement of A has a value of 1. Boolean notation uses a bar above the variable character to denote complementation, like this:

In written form, the complement of .A. denoted as .A-not. or .A-bar.. Sometimes a .prime.symbol is used to represent complementation. For example, A‘ would be the complement of A, much the same as using a prime symbol to denote differentiation in calculus rather than the fractional notation dot. Usually, though, the .bar. symbol finds more widespread use than the .prime. symbol, for reasons that will become more apparent later in this chapter.

2 Boolean Arithmetic:

Let us begin our exploration of Boolean algebra by adding numbers together:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 1

The first three sums make perfect sense to anyone familiar with elementary addition. The Last sum, though, is quite possibly responsible for more confusion than any other single statement in digital electronics, because it seems to run contrary to the basic principles of mathematics.

Well, it does contradict principles of addition for real numbers, but not for Boolean numbers. Remember that in the world of Boolean algebra, there are only two possible values for any quantity and for any arithmetic operation: 1 or 0. There is no such thing as .2. within the scope of  Boolean values. Since the sum .1 + 1. certainly isn‘t 0, it must be 1 by process of elimination.

2.1 Addition – OR Gate Logic:

Boolean addition corresponds to the logical function of an ||OR|| gate, as well as to parallel switch contacts:

 There is no such thing as subtraction in the realm of Boolean mathematics. Subtraction  Implies the existence of negative numbers: 5 - 3 is the same thing as 5 + (-3), and in Boolean algebra negative quantities are forbidden. There is no such thing as division in Boolean mathematics, either, since division is really nothing more than compounded subtraction, in the same way that multiplication is compounded addition.

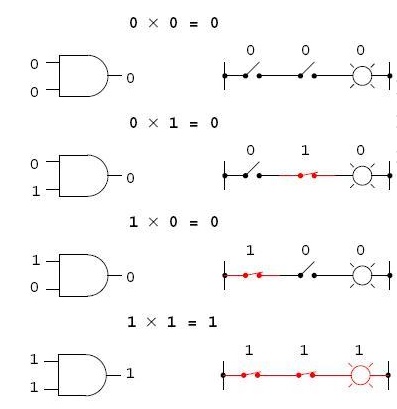
2.2 Multiplication – AND Gate logic

Multiplication is valid in Boolean algebra, and thankfully it is the same as in real-number algebra: anything multiplied by 0 is 0, and anything multiplied by 1 remains unchanged:

0 × 0 = 0

0 × 1 = 0

1 × 0 = 0

1 × 1 = 1

This set of equations should also look familiar to you: it is the same pattern found in the truth  table for an AND gate. In other words, Boolean multiplication corresponds to the logical  function of an .AND. gate, as well as to series switch contacts:

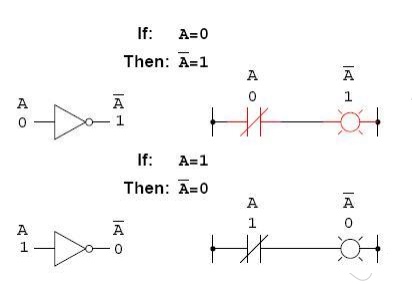
2.3 Complementary Function – NOT gate Logic

Boolean complementation finds equivalency in the form of the NOT gate, or a normally closed switch or relay contact:

3 Boolean Algebraic Identities

In mathematics, an identity is a statement true for all possible values of its variable or  variables. The algebraic identity of x + 0 = x tells us that anything (x) added to zero equals the original .anything,. no matter what value that .anything. (x) may be. Like ordinary algebra, Boolean algebra has its own unique identities based on the bivalent states of Boolean variables.

 The first Boolean identity is that the sum of anything and zero is the same as the original .anything.. This identity is no different from its real-number algebraic equivalent:

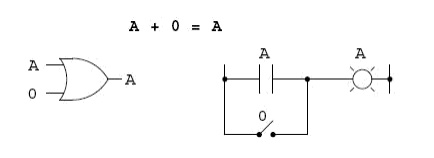
No matter what the value of A, the output will always be the same: when A=1, the output will also be 1; when A=0, the output will also be 0.

The next identity is most definitely different from any seen in normal algebra. Here

we discover that the sum of anything and one is one:

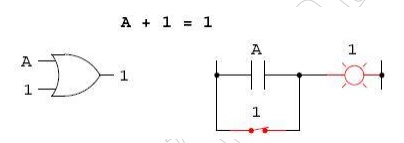
No matter what the value of A, the sum of A and 1 will always be 1. In a sense, the 1 signal overrides the effect of A on the logic circuit, leaving the output fixed at a logic level of 1. Next, we examine the effect of adding A and A together, which is the same as connecting both inputs of an OR gate to each other and activating them with the same signal:

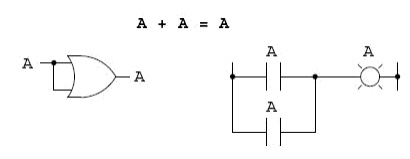
In real-number algebra, the sum of two identical variables is twice the original variable‘s  value (x + x = 2x), but remember that there is no concept of .2. in the world of Boolean math, only 1 and 0, so we cannot say that A + A = 2A. Thus, when we add a Boolean quantity to itself,  the sum is equal to the original quantity: 0 + 0 = 0, and 1 + 1 = 1.

Introducing the uniquely Boolean concept of complementation into an additive identity, we find an interesting effect. Since there must be one .1. value between any variable and its complement,  and since the sum of any Boolean quantity and 1 is 1, the sum of a variable and its complement  must be 1:

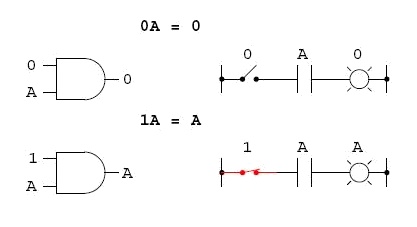
Four multiplicative identities: Ax0, Ax1, AxA, and AxA‘. Of these, the first two are no different from their equivalent expressions in regular algebra:

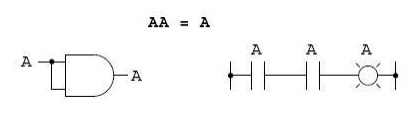
The third multiplicative identity expresses the result of a Boolean quantity multiplied by s itself. In normal algebra, the product of a variable and itself is the square of that variable (3x 3 =32 = 9). However, the concept of .square. implies a quantity of 2, which has no meaning in Boolean algebra, so we cannot say that A x A = A2. Instead, we find that the product of a Boolean quantity and itself is the original quantity, since 0 x 0 = 0 and 1 x 1 = 1:

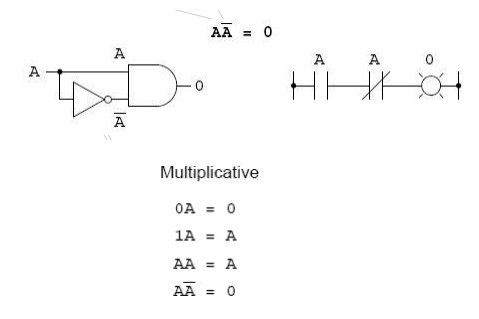
The fourth multiplicative identity has no equivalent in regular algebra because it uses the complement of a variable, a concept unique to Boolean mathematics. Since there must be one .0. value between any variable and its complement, and since the product of any Boolean quantity and 0 is 0, the product of a variable and its complement must be 0:

4 Principle of Duality:

 It states that every algebraic expression is deducible from the postulates of Boolean algebra, and it remains valid if the operators & identity elements are interchanged. If the inputs of a NOR gate are inverted we get a AND equivalent circuit. Similarly when the inputs of a NAND gate are inverted, we get a OR equivalent circuit. This property is called DUALITY.

5 Theorems of Boolean algebra:

The theorems of Boolean algebra can be used to simplify many a complex Boolean

expression and also to transform the given expression into a more useful and meaningful equivalent expression. The theorems are presented as pairs, with the two theorems in a given pair being the dual of each other. These theorems can be very easily verified by the method of =perfect induction‘. According to this method, the validity of the expression is tested for all possible combinations of values of the variables involved. Also, since the validity of the theorem

is based on its being true for all possible combinations of values of variables, there is no reason why a variable cannot be replaced with its complement, or vice versa, without disturbing the validity. Another important point is that, if a given expression is valid, its dual will also be valid

5.1 Theorem 1 (Operations with =0‘ and =1‘)

(a) 0.X = 0 and (b) 1+X= 1

Where X is not necessarily a single variable – it could be a term or even a large expression. Theorem 1(a) can be proved by substituting all possible values of X, that is, 0 and 1, into the given expression and checking whether the LHS equals the RHS:   

• For X = 0, LHS = 0.X = 0.0 = 0 = RHS.

• For X= 1, LHS = 0.1 = 0 = RHS.

Thus, 0.X =0 irrespective of the value of X, and hence the proof.

Theorem 1(b) can be proved in a similar manner. In general, according to theorem 1, 0. (Boolean expression) = 0 and 1+ (Boolean expression) =1.

For example: 0. (A.B+B.C +C.D) = 0 and 1+ (A.B+B.C +C.D) = 1, where A, B and C are Boolean variables.

5.2 Theorem 2 (Operations with =0‘ and =1‘)

(a) 1.X = X and (b) 0+X = X

where X could be a variable, a term or even a large expression. According to this theorem, AND ing a Boolean expression to =1‘ or ORing =0‘ to it makes no difference to the expression:

• For X = 0, LHS = 1.0 = 0 = RHS.

• For X = 1, LHS = 1.1 = 1 = RHS.

Also,

1. (Boolean expression) = Boolean expression and 0 + (Boolean expression) = Boolean expression.

For example,

1.(A+B.C +C.D) = 0+(A+B.C +C.D) = A+B.C +C.D

5.3 Theorem 3 (Idempotent or Identity Laws)

(a) X.X.X……X = X and (b) X+X+X +···+X = X

Theorems 3(a) and (b) are known by the name of idempotent laws, also known as identity laws. Theorem 3(a) is a direct outcome of an AND gate operation, whereas theorem 3(b) represents an OR gate operation when all the inputs of the gate have been tied together. The scope of idempotent laws can be expanded further by considering X to be a term or an expression. For

example, let us apply idempotent laws to simplify the following Boolean expression:

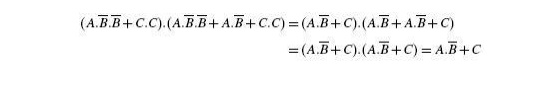
5.4 Theorem 4 (Complementation Law)

 (a) X-X = 0 and (b) X+X = 1

According to this theorem, in general, any Boolean expression when ANDed to its complement yields a =0‘ and when ORed to its complement yields a =1‘, irrespective of the complexity of the expression:

Hence, theorem 4(a) is proved. Since theorem 4(b) is the dual of theorem 4(a), its proof is implied. The example below further illustrates the application of complementation laws:

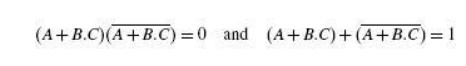
5.5 Theorem 5 (Commutative property)

 Mathematical identity, called a .property. or a .law,. describes how differing

variables relate to each other in a system of numbers. One of these properties is known as the commutative property, and it applies equally to addition and multiplication. In essence, the  commutative property tells us we can reverse the order of variables that are either added together or multiplied together without changing the truth of the expression:

Commutative property of addition

A + B = B + A

Commutative property of multiplication

AB = BA

5.6 Theorem 6 (Associative Property)

The Associative Property, again applying equally well to addition and multiplication.This property tells us we can associate groups of added or multiplied variables together with parentheses without altering the truth of the equations.

Associative property of addition

A + (B + C) = (A + B) + C

Associative property of multiplication

A (BC) = (AB) C

5.7 Theorem 7 (Distributive Property)

 The Distributive Property, illustrating how to expand a Boolean expression formed by theproduct of a sum, and in reverse shows us how terms may be factored out of Boolean sums-of-products:

Distributive property

A (B + C) = AB + AC

5.8 Theorem 8 (Absorption Law or Redundancy Law)

(a) X+X.Y = X and (b) X.(X+Y) = X

The proof of absorption law is straightforward:

X+X.Y = X. (1+Y) = X.1 = X

Theorem 8(b) is the dual of theorem 8(a) and hence stands proved.

The crux of this simplification theorem is that, if a smaller term appears in a larger term, then the larger term is redundant. The following examples further illustrate the underlying concept:

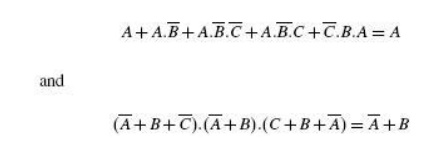
5.9 Demorgan‘s Theorem

 De-Morgan was a great logician and mathematician. He had contributed much to logic.

Among his contribution the following two theorems are important

5.9.1 De-Morgan‘s First Theorem

 It States that .The complement of the sum of the variables is equal to the product of the complement of each variable.. This theorem may be expressed by the following Boolean expression.

5.9.2 De-Morgan‘s Second Theorem 

It states that the .Complement of the product of variables is equal to the sum of complements of each individual variables.. Boolean expression for this theorem is

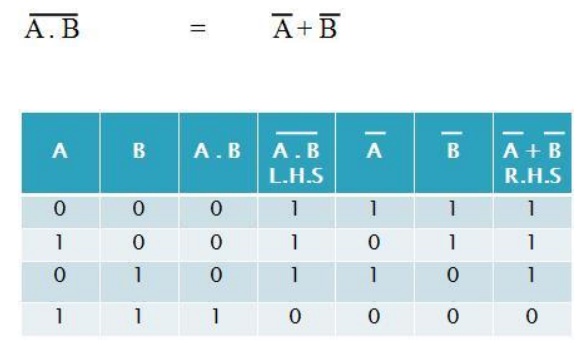
1.6 Boolean function

Z=AB‘+A‘C+A‘B‘C‘

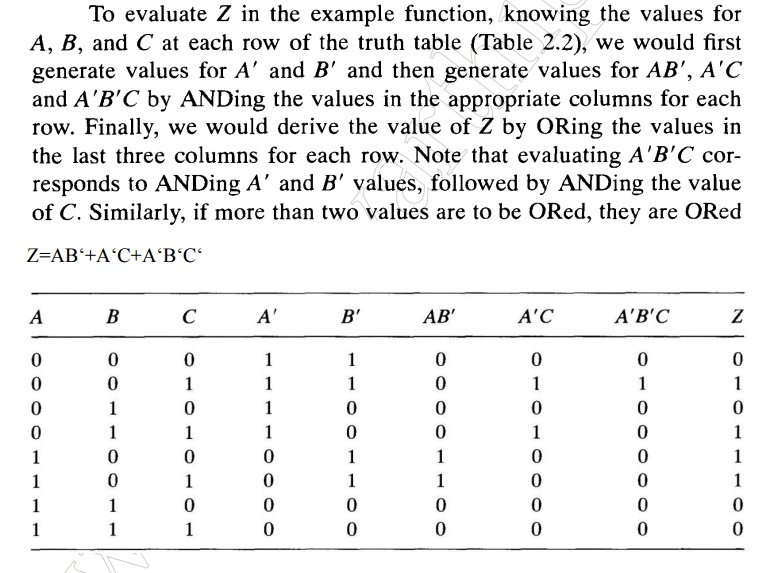
7 Canonical Form of Boolean Expressions

 An expanded form of Boolean expression, where each term contains all Boolean variables in their true or complemented form, is also known as the canonical form of the expression. As an illustration, is a Boolean function of three variables expressed in canonical form. This function after simplification reduces to and loses its canonical form.

7.1 MIN TERMS AND MAX TERMS

 Any boolean expression may be expressed in terms of either minterms or maxterms. To do this we must first define the concept of a literal. A literal is a single variable within a term which may or may not be complemented. For an expression with N variables, minterms and maxterms are defined as follows :

• A minterm is the product of N distinct literals where each literal occurs exactly once.

• A maxterm is the sum of N distinct literals where each literal occurs exactly

once. Product-of-Sums Expressions

7.2 Standard Forms

 A product-of-sums expression contains the product of different terms, with each term being either a single literal or a sum of more than one literal. It can be obtained from the truth table by considering those input combinations that produce a logic =0‘ at the output. Each such input combination gives a term, and the product of all such terms gives the expression. Different terms are obtained by taking the sum of the corresponding literals. Here, =0‘ and =1‘ respectively

mean the uncomplemented and complemented variables, unlike sum-of-products expressions where =0‘ and =1‘ respectively mean complemented and uncomplemented variables.

Since each term in the case of the product-of-sums expression is going to be the sum of literals, this implies that it is going to be implemented using an OR operation. Now, an OR gate produces a logic =0‘ only when all its inputs are in the logic =0‘ state, which means that the first term corresponding to the second row of the truth table will be A+B+C. The product-of-sums Boolean expression for this truth table is given by Transforming the given product-of-sums expression

into an equivalent sum-of-products expression is a straightforward process. Multiplying out the given expression and carrying out the obvious simplification provides the equivalent sum-of-products expression:

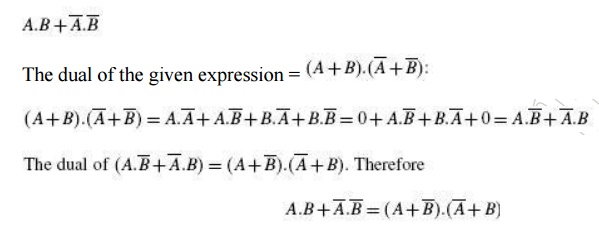
A given sum-of-products expression can be transformed into an equivalent product-of-sums expression by (a) taking the dual of the given expression, (b) multiplying out different terms to get the sum-of products form, (c) removing redundancy and (d) taking a dual to get the equivalent product-of-sums expression. As an illustration, let us find the equivalent product-of-sums expression of the sum-of products expression The dual of the given expression = 

8 Minimization Technique  

The primary objective of all simplification procedures is to obtain an expression that has the minimum number of terms. Obtaining an expression with the minimum number of literals is usually the secondary objective. If there is more than one possible solution with the same number of terms, the one having the minimum number of literals is the choice.

There are several methods for simplification of Boolean logic expressions. The process is usually called logic minimization. and the goal is to form a result which is efficient. Two methods we will discuss are algebraic minimization and Karnaugh maps. For very complicated problems the former method can be done using special software analysis programs. Karnaugh maps are also limited to problems with up to 4 binary inputs. The Quine–McCluskey tabular method is used for more than 4 binary inputs.

9 Karnaugh Map Method

Maurice Karnaugh, a telecommunications engineer, developed the Karnaugh map at Bell Labs in 1953 while designing digital logic based telephone switching circuits.Karnaugh maps reduce logic functions more quickly and easily compared to Boolean algebra. By reduce we mean simplify, reducing the number of gates and inputs. We like to simplify logic to a lowest cost form to save costs by elimination of components. We define lowest cost as being the lowest number of gates with the lowest number of inputs per gate.

 A Karnaugh map is a graphical representation of the logic system. It can be drawn directly from either minterm (sum-of-products) or maxterm (product-of-sums) Boolean expressions. Drawing a Karnaugh map from the truth table involves an additional step of writing the minterm or maxterm expression depending upon whether it is desired to have a minimized sum-of-products or a minimized product of-sums expression.

9.1 Construction of a Karnaugh Map

 An n-variable Karnaugh map has 2n squares, and each possible input is allotted a square. In the case of a minterm Karnaugh map, =1‘ is placed in all those squares for which the output is =1‘, and =0‘ is placed in all those squares for which the output is =0‘. 0s are omitted for simplicity. An =X‘ is placed in squares corresponding to =don‘t care‘ conditions. In the case of a maxterm Karnaugh map, a =1‘ is placed in all those squares for which the output is =0‘, and a =0‘ is placed for input entries corresponding to a =1‘ output. Again, 0s are omitted for simplicity, and an =X‘ is placed in squares corresponding to =don‘t care‘ conditions. The choice of terms identifying different rows and columns of a Karnaugh map is not unique for a given number of variables. The only condition to be satisfied is that the designation of adjacent rows and adjacent columns should be the same except for one of the literals being complemented. Also, the extreme rows and extreme columns are considered adjacent.

 Some of the possible designation styles for two-, three- and four-variable minterm Karnaugh maps are shown in the figure below.

The style of row identification need not be the same as that of column identification as long as it meets the basic requirement with respect to adjacent terms. It is, however, accepted practice to adopt a uniform style of row and column identification. Also, the style shown in the figure below is more commonly used. A similar discussion applies for maxterm Karnaugh maps. Having drawn the Karnaugh map, the next step is to form groups of 1s as per the following guidelines:

 1. Each square containing a =1‘ must be considered at least once, although it can be considered as often as desired.

2. The objective should be to account for all the marked squares in the minimum number of groups.

3. The number of squares in a group must always be a power of 2, i.e. groups can have 1,2, 4, 8, 16, squares.

4. Each group should be as large as possible, which means that a square should not be accounted for by itself if it can be accounted for by a group of two squares; a group of two squares should not be made if the involved squares can be included in a group of four squares and so on.

5. =Don‘t care‘ entries can be used in accounting for all of 1-squares to make optimum groups. They are marked =X‘ in the corresponding squares. It is, however, not necessary to account for all =don‘t care‘ entries. Only such entries that can be used to advantage should be used.

Fig 1.9.1 Two variable K Map

Fig 1.9.2 Three variable K Map

Fig 1.9.3 Four variable K Map

Fig 1.9.4 Different Styles of row and column identification

 Having accounted for groups with all 1s, the minimum =sum-of-products‘ or =product-of-sums‘ expressions can be written directly from the Karnaugh map. Minterm Karnaugh map and Maxterm Karnaugh map of the Boolean function of a two-input OR gate. The Minterm and Maxterm Boolean expressions for the two-input OR gate are as follows:

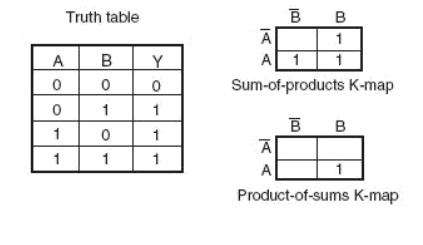
           Minterm Karnaugh map and Maxterm Karnaugh map of the three variable Boolean function

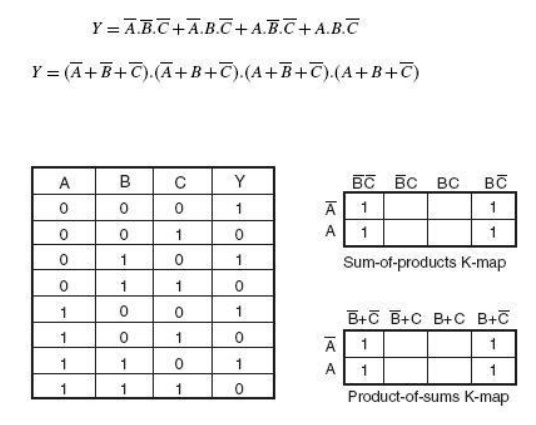
The truth table, Minterm Karnaugh map and Maxterm Karnaugh map of the four

variable Boolean function

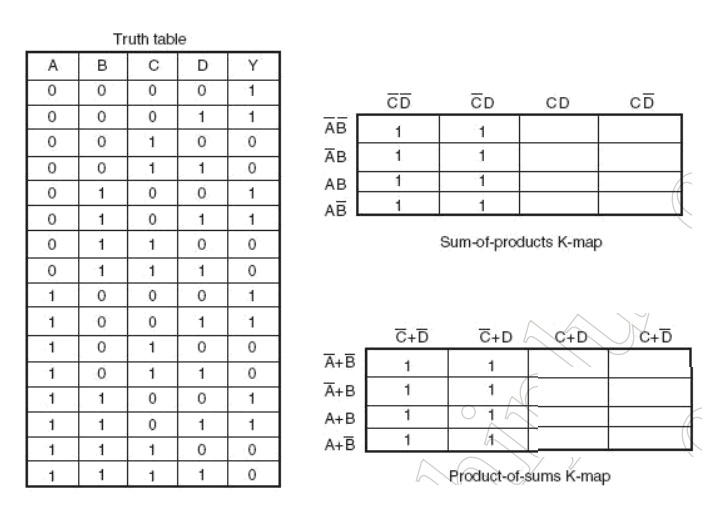
To illustrate the process of forming groups and then writing the corresponding minimized Boolean expression, The below figures respectively show minterm and maxterm Karnaugh maps for the Boolean functions expressed by the below equations. The minimized expressions as deduced from Karnaugh maps in the two cases are given by Equation in the case of the minterm Karnaugh map and Equation in the case of the maxterm Karnaugh map:

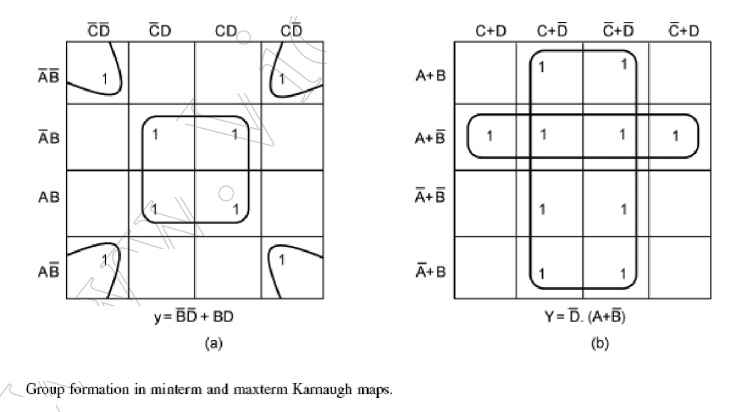
10 Quine–McCluskey Tabular Method

 The Quine–McCluskey tabular method of simplification is based on the complementation theorem, which says that 

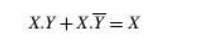
where X represents either a variable or a term or an expression and Y is a variable. This theorem implies that, if a Boolean expression contains two terms that differ only in one variable, then they can be combined together and replaced with a term that is smaller by one literal. The same procedure is applied for the other pairs of terms wherever such a reduction is possible. All these terms reduced by one literal are further examined to see if they can be reduced further. The process continues until the terms become irreducible. The irreducible terms are called prime implicants. An optimum set of prime implicants that can account for all the original terms then constitutes the minimized expression. The technique can be applied equally well for minimizing sum-of-products and product of- sums expressions and is particularly useful for Boolean functions having more than six variables as it can be mechanized and run on a computer. On the other hand, the Karnaugh mapping method, to be discussed later, is a graphical method and becomes very cumbersome when the number of variables exceeds six. The step-by-step procedure for application of the tabular method for minimizing Boolean expressions,both sum-of-products and product-of-sums, is outlined as follows:

1. The Boolean expression to be simplified is expanded if it is not in expanded form.

2. Different terms in the expression are divided into groups depending upon the number of 1s they have.

 True and complemented variables in a sum-of-products expression mean =1‘ and =0‘ respectively.

 The reverse is true in the case of a product-of-sums expression. The groups are then arranged, beginning with the group having the least number of 1s in its included terms. Terms within the same group are arranged in ascending order of the decimal numbers represented by these terms. As an illustration, consider the expression

 As another illustration, consider a product-of-sums expression given by

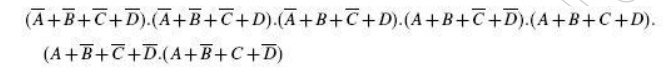
The formation of groups and the arrangement of terms within different groups for the product-of sums expression are as follows:

It may be mentioned here that the Boolean expressions that we have considered above did not contain any optional terms. If there are any, they are also considered while forming groups. This completes the first table.

3. The terms of the first group are successively matched with those in the next adjacent higher order group to look for any possible matching and consequent reduction. The terms are considered matched when all literals except for one match. The pairs of matched terms are replaced with a single term where the position of the unmatched literals is replaced with a dash (—). These new terms formed as a result of the matching process find a place in the second table. The terms in the first table that do not find a match are called the prime implicants and are marked with an asterisk (*). The matched terms are ticked (_).

4. Terms in the second group are compared with those in the third group to look for a possible match. Again, terms in the second group that do not find a match become the prime implicants.

 5. The process continues until we reach the last group. This completes the first round of matching. The terms resulting from the matching in the first round are recorded in the second table.

 6. The next step is to perform matching operations in the second table. While comparing the terms for a match, it is important that a dash (—) is also treated like any other literal, that is, the dash signs also need to match. The process continues on to the third table, the fourth table and so on until the terms become irreducible any further.

7. An optimum selection of prime implicants to account for all the original terms constitutes the terms for the minimized expression. Although optional (also called =don‘t care‘) terms are considered for matching, they do not have to be accounted for once prime implicants have been identified.

Let us consider an example. Consider the following sum-of-products expression:

The second round of matching begins with the table shown on the previous page.

Each term in the first group is compared with every term in the second group. For instance, the first term in the first group 00-1 matches with the second term in the second group 01-1 to yield 0--1, which is recorded in the table shown below. The process continues until all terms have been compared for a possible match. Since this new table has only one group, the terms contained therein are all prime implicants. In the present example, the terms in the first and second tables have all found a match. But that is not always the case.

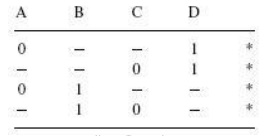
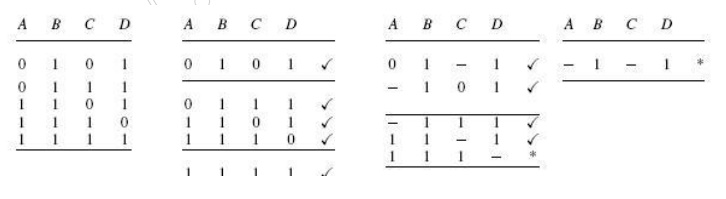
The next table is what is known as the prime implicant table. The prime implicant table contains all the original terms in different columns and all the prime implicants recorded in different rows as shown below:

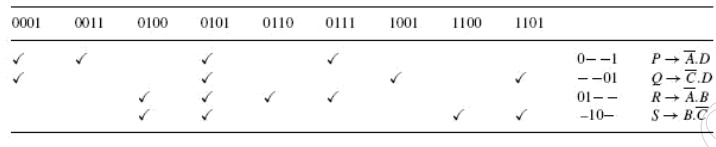
Each prime implicant is identified by a letter. Each prime implicant is then examined one by one and the terms it can account for are ticked as shown. The next step is to write a product-of-sums expression using the prime implicants to account for all the terms. In the present illustration, it is given as follows.

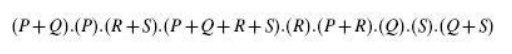
 Obvious simplification reduces this expression to PQRS which can be interpreted to mean that all prime implicants, that is, P, Q, R and S, are needed to account for all the original terms.

Therefore, the minimized expression =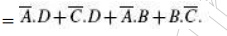 

What has been described above is the formal method of determining the optimum set of prime implicants. In most of the cases where the prime implicant table is not too complex, the exercise can be done even intuitively. The exercise begins with identification of those terms that can be accounted for by only a single prime implicant. In the present example, 0011, 0110, 1001 and 1100 are such terms. As a result, P, Q, R and S become the essential prime implicants. The next step is to find out if any terms have not been covered by the essential prime implicants. In the

present case, all terms have been covered by essential prime implicants. In fact, all prime implicants are essential prime implicants in the present example. As another illustration, let us consider a product-of-sums expression given by

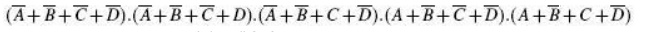
 The procedure is similar to that described for the case of simplification of sum-of-products expressions.

The resulting tables leading to identification of prime implicants are as follows:

The prime implicant table is constructed after all prime implicants have been identified to look for the optimum set of prime implicants needed to account for all the original terms. The prime implicant table shows that both the prime implicants are the essential ones:

11 Universal Gates

 OR, AND and NOT gates are the three basic logic gates as they together can be used to construct the logic circuit for any given Boolean expression. NOR and NAND gates have the property that they individually can be used to hardware-implement a logic circuit corresponding to any given Boolean expression. That is, it is possible to use either only NAND gates or only NOR gates to implement any Boolean expression. This is so because a combination of NAND gates or a combination of NOR gates can be used to perform functions of any of the basic logic gates. It is for this reason that NAND and NOR gates are universal gates. As an illustration, Fig. 4.24 shows how two-input NAND gates can be used to construct a NOT circuit, a two-input AND gate and a two-input OR gate. Figure

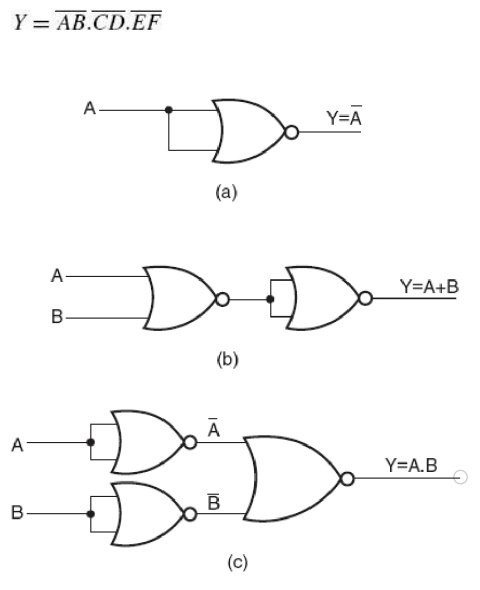
shows the same using NOR gates. Understanding the conversion of NAND to OR and NOR to AND requires the use of DeMorgan‘s theorem, which is discussed in Chapter 6 on Boolean algebra.

These are gates where we need to connect an external resistor, called the pull-up resistor, between the output and the DC power supply to make the logic gate perform the intended logic function. Depending on the logic family used to construct the logic gate, they are referred to as gates with open collector output (in the case of the TTL logic family) or open drain output (in the case of the MOS logic family). 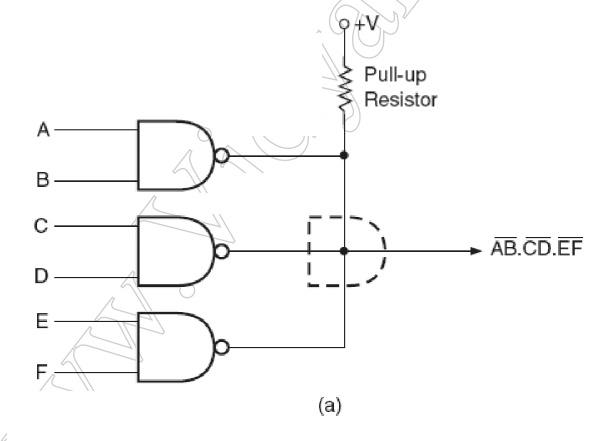Logic families are discussed in detail in Chapter 5. The advantage of using open collector/open drain gates lies in their capability of providing an

ANDing operation when outputs of several gates are tied together through a common pull-up resistor,

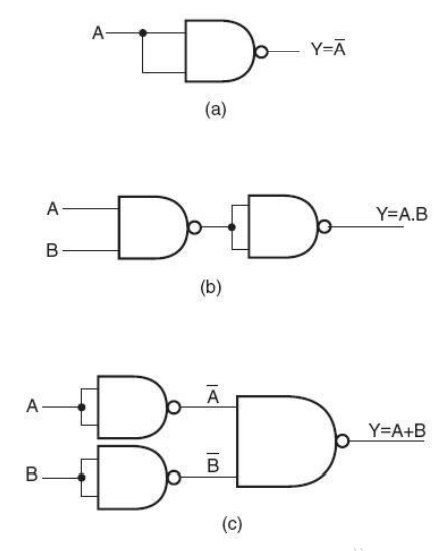
Fig 1.11.1 Implementation of basic logic gates using only NAND gates

without having to use an AND gate for the purpose. This connection is also referred to as WIRE-AND connection. Figure shows such a connection for open collector NAND gates. The output in this case would be

WIRE-AND connection with open collector/drain devices.

The disadvantage is that they are relatively slower and noisier. Open collector/drain devices are therefore not recommended for applications where speed is an important consideration.

 The Exclusive-OR function

One element conspicuously missing from the set of Boolean operations is that of Exclusive-OR. Whereas the OR function is equivalent to Boolean addition, the AND function to Boolean multiplication, and the NOT function (inverter) to Boolean complementation, there is no direct Boolean equivalent for Exclusive-OR. This hasn‘t stopped people from developing a symbol to represent it, though:

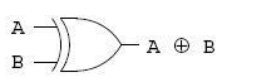
This symbol is seldom used in Boolean expressions because the identities, laws, and rules of simplification involving addition, multiplication, and complementation do not apply to it. However, there is a way to represent the Exclusive-OR function in terms of OR and AND, as has been shown in previous chapters: AB‘ + A‘B.