Boolean Algebra and Theorems

BOOLEAN ALGEBRA AND THEOREMS

In 1854, George Boole developed an algebraic system now called Boolean algebra. In 1938, C. E. Shannon introduced a two-valued Boolean algebra called switching algebra that represented the properties of bistable electrical switching circuits.

Boolean algebra is an algebraic structure defined by a set of elements B, together with two binary operators. ‘+’ and-‘, provided‘ that the following (Huntington) postulates are satisfied;

Principle of Duality

It states that every algebraic expression is deducible from the postulates of Boolean algebra, and it remains valid if the operators & identity elements are interchanged. If the inputs of a NOR gate are inverted we get a AND equivalent circuit. Similarly when the inputs of a NAND gate are inverted, we get a OR equivalent circuit.

1.    Interchanging the OR and AND operations of the expression.

2.    Interchanging the 0 and 1 elements of the expression.

3.    Not changing the form of the variables.

Theorems of Boolean algebra:

The theorems of Boolean algebra can be used to simplify many a complex Boolean expression and also to transform the given expression into a more useful and meaningful equivalent expression. The theorems are presented as pairs, with the two theorems in a given pair being the dual of each other. These theorems can be very easily verified by the method of ‗perfect induction‘. According to this method, the validity expression is tested for all possible combinations of values of the variables involved. Also, since the validity of the theorem is based on its being true for all possible combinations of values of variables, there is no reason why a variable cannot be replaced with its complement, or vice versa, without disturbing the validity. Another important point is that, if a given expression is valid, its dual will also be valid.

T1: Commutative Law

(a)           A + B = B + A

(b)           A B = B A

T2: Associative Law

(a) (A + B) + C = A + (B + C)

(b) (A B) C = A (B C)

T3: Distributive Law

(a)     A (B + C) = A B + A C

(b)     A + (B C) = (A + B) (A + C)

T4: Identity  Law

(a)               A + A = A

(b)               A A = A

T10: De Morgan's Theorem

Order of Precedence

NOT operations have the highest precedence, followed by AND operations, followed by OR operations. Brackets can be used as with other forms of algebra.

e.g.    X.Y + Z and X.(Y + Z) are not the same function.

Truth Tables

Truth tables are a means of representing the results of a logic function using a table. They are constructed by defining all possible combinations of the inputs to a function, and then calculating the output for each combination in turn.

Minterms and maxterms

A binary variable may appear either in its normal form (x) or in its complement form (x' ). Now consider two binary variables x and y combined with an AND operation. Since each variable may appear in either form, there are four possible combinations: x' y', x'y. xy ' , and xy. Each of these four AND term s is called a minterm, or a standard product.

In a similar fashion, n variables forming g an OR terrn with each variable being primed or Unprimed provide 2" possible combinations called maxterm. or standard sums.

•                     A minterm is the product of N distinct literals where each literal occurs exactly once.

•                     A maxterm is the sum of N distinct literals where each literal occurs exactly once.

For a two-variable expression, the minterms and maxterms are as follows

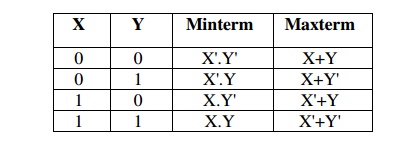
For a three-variable expression, the minterms and maxterms are as follows

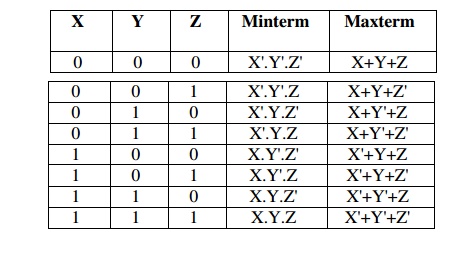
This allows us to represent expressions in either Sum of Products or Product of Sums forms

Sum Of Products (SOP): F(X, Y, ...) = Sum (a_k.m_k), where a_k is 0 or 1 and m_k is a minterm.

To derive the Sum of Products form from a truth table, OR together all of the minterms which give a value of 1.Consider the truth table as example,

Here SOP is f(X.Y) = X.Y' + X.Y

Product Of Sum (POS): The Product of Sums form represents an expression as a product of maxterms.F(X, Y, .......) = Product (b_k + M_k), where b_k is 0 or 1 and M_k is a maxterm. To derive the Product of Sums form from a truth table, AND together all of the maxterms which give a value of 0.Consider the truth table from the previous example

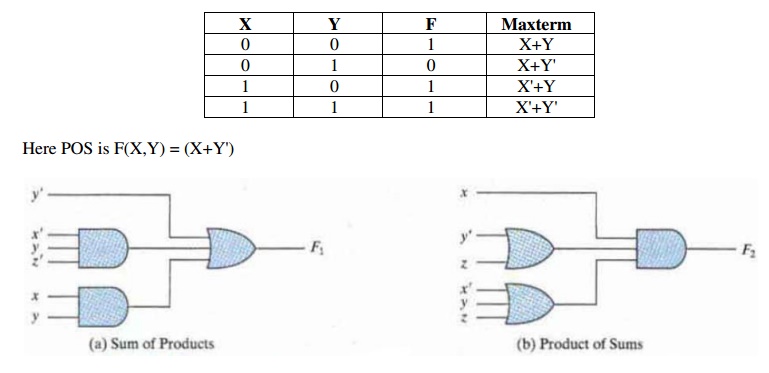
Conversion between POS and SOP: Conversion between the two forms is done by application of DeMorgans Laws.

Ref: 1)  A.P  Godse  &  D.A  Godse  “Digital  Electronics”,  Technical  publications,  Pune,  Revised edition, 2008. Pg.No:2.1-2.10

2)  Morris  Mano  M.  and  Michael  D.  Ciletti,  “Digital  Design”,  IV  Edition,  Pearson  Education 2008.Pg.No:36-44.