Quine-Mccluskey Method or Tabular method of minimization of logic functions

QUINE- MCCLUSKEY METHOD

The  tabular method which is also known as the Quine-McCluskey method is particularly useful when minimising functions having a large number of variables, e.g. The six-variable functions. Computer programs have been developed employing this algorithm. The method reduces a function in standard sum of products form to a set of prime implicants from which as many variables are eliminated as possible. These prime implicants are then examined to see if some are redundant.

The tabular method makes repeated use of the law

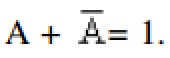
Note that Binary notation is used for the function, although decimal notation is also used for the functions. As usual a variable in true form is denoted by 1, in inverted form by 0, and the abscence of a variable by a dash ( - ).

Rules of Tabular Method

1.     The Boolean expression to be simplified is expanded if it is not in expanded form.

2.     Different terms in the expression are divided into groups depending upon the number of 1s they have.

3.     The terms of the first group are successively matched with those in the next adjacent higher order group to look for any possible matching and consequent reduction. The terms are considered

matched when all literals except for one match. The pairs of matched terms are replaced with a single term where the position of the unmatched literals is replaced with a dash (— ). These new terms_∗ formed as a result of the matching process find a place in the second table. The terms in the first table that do not find a match are called the prime implicants and are marked with an asterisk ( ). The matched terms are ticked (_).

4.     Terms in the second group are compared with those in the third group to look for a possible match.

Again, terms in the second group that do not find a match become the prime implicants.

5.     The process continues until we reach the last group. This completes the first round of matching. The terms resulting from the matching in the first round are recorded in the second table.

6.     The next step is to perform matching operations in the second table. While comparing the terms for a match, it is important that a dash (— ) is also treated like any other literal, that is, the dash signs also need to match. The process continues on to the third table, the fourth tables and so on until the terms become irreducible any further.

7.     An optimum selection of prime implicants to account for all the original terms constitutes the

terms for the minimized expression. Although optional (also called ‗do ‘t care‘) ter s are considered for matching, they do not have to be accounted for once prime implicants have been identified.

Example 1: Let us consider an example. Consider the following sum-of-products expression:

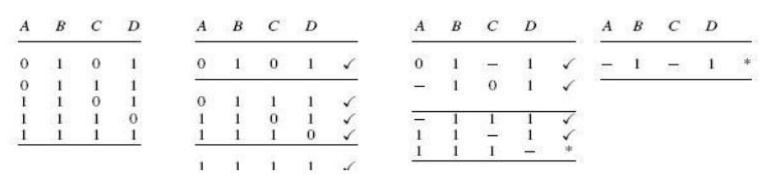
The second round of matching begins with the table shown on the previous page. Each term in the first

group is compared with every term in the second group. For instance, the first term in the first group

00−1 matches with the second term in the second group 01−1 to−1,yieldwhich is0−recorded in the table shown below. The process continues until all terms have been compared for a possible match. Since this new table has only one group, the terms contained therein are all prime implicants.

In the present example, the terms in the first and second tables have all found a match. But that is not always the case.

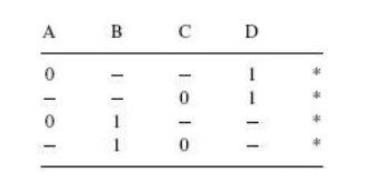
The next table is what is known as the prime implicant table. The prime implicant table contains all the original terms in different columns and all the prime implicants recorded in different rows as shown below:

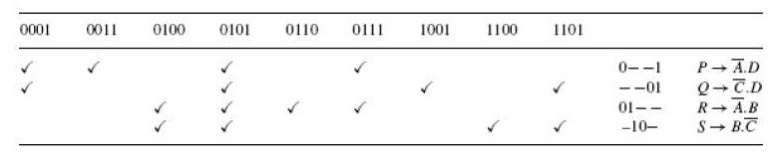
Each prime implicant is identified by a letter. Each prime implicant is then examined one by one and the terms it can account for are ticked as shown. The next step is to write a product-of-sums expression using the prime implicants to account for all the terms. In the present illustration, it is given as follows.

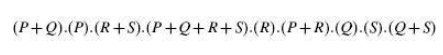
Obvious simplification reduces this expression to PQRS which can be interpreted to mean that all prime implicants, that is, P, Q, R and S, are needed to account for all the original terms.

Therefore, the minimized expression =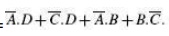 

Example 2:

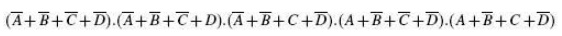
The procedure is similar to that described for the case of simplification of sum-of-products expressions. The resulting tables leading to identification of prime implicants are as follows:

The prime implicant table is constructed after all prime implicants have been identified to look for the optimum set of prime implicants needed to account for all the original terms. The prime implicant table shows that both the prime implicants are the essential ones:

The chart  is used to remove redundant prime implicants. A grid is prepared having all the prime implicants  listed at the left and all the minterms of the function along the top. Each minterm  covered by a  given prime implicant is marked in the appropriate position.

Ref: John F. Wakerly, “Digital Design Principles and Practices”,FourthEdition, Pearson Education,2007. Pg.No:264.