Binary codes

BINARY CODES

 

Binary codes are codes which are represented in binary system with modification from the original ones. There are two types of binary codes: Weighted codes and Non-Weighted codes. BCD and the 2421 code are examples of weighted codes. In a weighted code, each bit position is assigned a weighting factor in such a way that each digit ca n be evaluated by adding the weight of all the 1’s the in coded combination.

 

 

·       Weighted Binary Systems

 

ü    8421  code/BCD code

 

The BCD  (Binary Coded Decimal) is a straight assignment of the binary equivalent.  It is possible to  assign weights to the binary bits according to their positions.  The weights in the BCD code are 8,4,2,1.

 

Example: The bit assignment 1001, can be seen by its weights to represent the decimal 9 because 1x8+0x4+0x2+1x1 = 9

 

Weighted Code

 

– 8421 code

•     Most common

•     Default

•      The corresponding decimal  digit  is  determined  by adding the  weights  associated with  t

code group.

– 62310 = 0110 0010 0011

– 2421, 5421,7536, etc… codes

• The weights associated with the bits in each code group are given by the name of the code

 

Nonweighted Codes

 

– 2-out-of-5

 

Non Weighted codes are codes that are not positionally weighted. That is, each position within the binary number is not assigned a fixed value.

•     Actually weighted 74210 except for the digit 0

•     Used by the post office for scanning bar codes for zip codes

•     Has error detection properties

 

ü      2421 code

 

This is a weighted code; its weights are 2, 4, 2 and 1. A decimal number is represented in 4-bit form and the total four bits weight is 2 + 4 + 2 + 1 = 9. Hence the 2421 code represents the decimal numbers from 0 to 9.

 

ü    5211 code

 

This is a weighted code; its weights are 5, 2, 1 and 1. A decimal number is represented in 4-bit form and the total four bits weight is 5 + 2 + 1 + 1 = 9. Hence the 5211 code represents the decimal numbers from 0 to 9.

 

ü    Reflective code

 

A code is said to be reflective when code for 9 is complement for the code for 0, and so is for 8 and 1 codes, 7 and 2, 6 and 3, 5 and 4. Codes 2421, 5211, and excess-3 are reflective, whereas the 8421 code is not.

 

ü    Sequential code

 

The BCD  (Binary Coded Decimal) is a straight assignment of the binary equivalent.  It is possible to  assign weights to the binary bits according to their positions.  The weights in the BCD code are 8,4,2,1.

 

ü    Excess- 3 code

 

Excess-3  is a non weighted code used to express decimal numbers. The code derives its  name from  the fact that each binary code is the corresponding 8421 code plus  0011(3).

 

Example:  1000 of 8421 = 1011 in  Excess-3

 

ü    Gray code

 

The gray code belongs to a class of codes called minimum change codes, in which only one bit in the code changes when moving from one code to the next. The Gray code is non-weighted code, as the position of bit does not contain any weight. In digital Gray code has got a special place.

 

Decimal      Binary Code        Gray Code

Number

0        0000  0000

1        0001  0001

2        0010  0011

3        0011  0010

4        0100  0110

5        0101  0111

6        0110  0101

7        0111  0100

8        1000  1100

9        1001  1101

10      1010  1111

11      1011  1110

12      1100  1010

13      1101  1011

14      1110  1001

15      1111  1000

 

The gray code is a reflective digital code which has the special property that any two subsequent numbers codes differ by only one bit. This is also called a unit-distance code.

 

Important when an analog quantity must be converted to a digital representation. Only one bit changes between two successive integers which are being coded.

 

ü    Error Detecting and Correction Codes

 

·                    Error detecting  codes

 

When  data is transmitted from one point to another, like in wireless transmission, or it is just  stored,  like in hard disks and memories, there are chances that data may get  corrupted. To detect these data  errors, we use special codes, which are error detection  codes.

 

·                    Error correcting code

 

Error-correcting codes not only detect errors, but also correct them. This is used normally in Satellite communication, where turn-around delay is very high as is the probability of data getting corrupt.

 

·                    Hamming codes

 

Hamming code adds a minimum number of bits to the data transmitted in a noisy channel, to be able to correct every possible one-bit error. It can detect (not correct) two-bit errors and cannot distinguish between 1-bit and 2-bits inconsistencies. It can't - in general - detect 3(or more)-bits errors.

 

·                    Parity codes

 

A parity bit is an extra bit included with a message to make the total number of 1’s either parity codes, every data byte, or nibble (according to how user wants to use it) is checked if they have even number of ones or even number of zeros. Based on this information an additional bit is appended to the original data. Thus if we consider 8-bit data, adding the parity bit will make it 9 bit long.

 

At the receiver side, once again parity is calculated and matched with the received parity (bit 9), and if they match, data is ok, otherwise data is corrupt.

 

Two types of parity

 

-Even parity: Checks if there is an even number of ones; if so, parity bit is zero. When the number of one’sis odd then parity bit is set to 1.

 

-Odd Parity: Checks if there is an odd number of ones; if so, parity bit is zero. When the number of one’sis even then parity bit is set to 1.

 

ü    Alphanumeric  codes

 

The binary  codes that can be used to represent all the letters of the alphabet, numbers  and  mathematical symbols, punctuation marks, are known as alphanumeric  codes or character codes. These  codes enable us to interface the input-output  devices like the keyboard, printers, video displays with the computer.

 

 

·                    ASCII codes

 

Codes to handle alphabetic and numeric information, special symbols, punctuation marks, and control characters.

 

• ASCII (American Standard Code Information Interchange) is the best known.

• Unicode –a 16-bit coding system provides for foreign languages, mathematical symbols, geometrical shapes, dingbats, etc. It has become a  world standard alphanumeric code for microcomputers and computers. It is a 7-bit  code representing 2⁷ = 128 different characters. These characters represent  26  upper case letters (A to Z), 26 lowercase letters (a to z), 10 numbers  (0 to 9), 33 special characters and  symbols and 33 control characters.

 

 

·                    EBCDIC  codes

 

EBCDIC stands for Extended Binary Coded Decimal Interchange. It is mainly used with large computer systems like mainframes. EBCDIC is an 8-bit code and thus accommodates up to 256 characters. An EBCDIC code is divided into two portions: 4 zone bits (on the left) and 4 numeric bits (on the right).

 

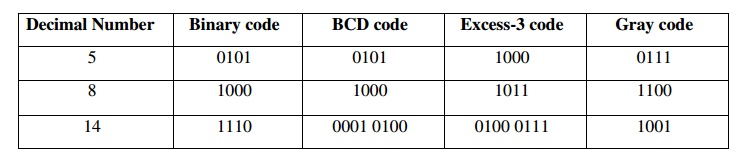
Example 1: Give the binary, BCD, Excess-3, gray code representations of numbers: 5,8,14.

 

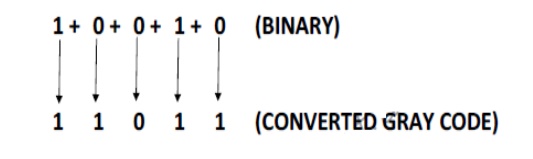
Example 2: Binary To Gray Code Conversion

 

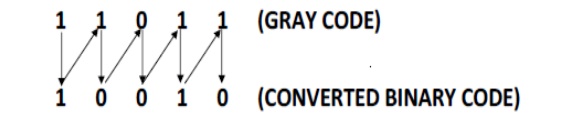
Example 3: Gray Code To Binary Code Conversion

Ref: 1)  A.P  Godse  &  D.A  Godse  “Digital  Electronics”,  Technical  publications,  Pune,  Revised edition, 2008. Pg.No:31-57.

2)  Morris  Mano  M.  and  Michael  D.  Ciletti,  “Digital  Design”,  IV  Edition,  Pearson  Education

2008.Pg.No:17-24

3) John F. Wakerly, “Digital Design Principles and Practices”, Fourth Edition, Pearson Education Pg.No:44-60.