NAND and NOR implementation

NAND and NOR implementation

Any logic function can be implemented using NAND gates. To achieve this, first the logic function has to be written in Sum of Product (SOP) form. Once logic function is converted to SOP, then is very easy to implement using NAND gate. In other words any logic circuit with AND gates in first level and OR gates in second level can be converted into a NAND-NAND gate circuit.

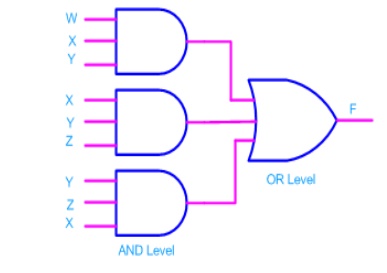
Consider the following SOP expression

F = W.X.Y + X.Y.Z + Y.Z.W

The above expression can be implemented with three AND gates in first stage and one OR gate in second stage as shown in figure.

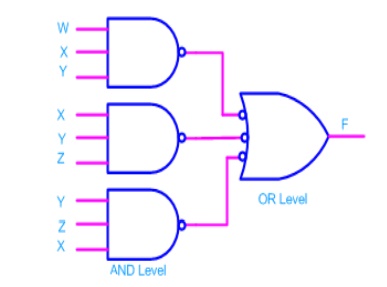
If bubbles are introduced at AND gates output and OR gates inputs (the same for NOR gates), the above circuit becomes as shown in figure.

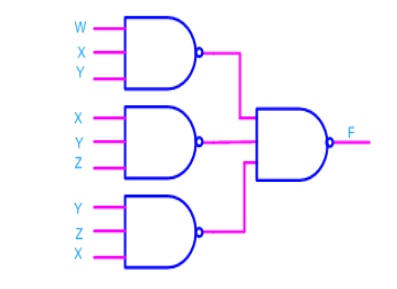
Now replace OR gate with input bubble with the NAND gate. Now we have circuit which is fully implemented with just NAND gates.

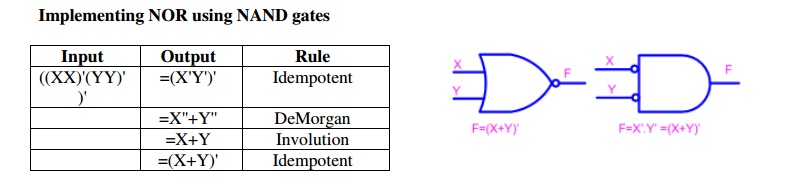
ü      Realization of logic gates using NAND gates

Implementing an inverter using NAND gate

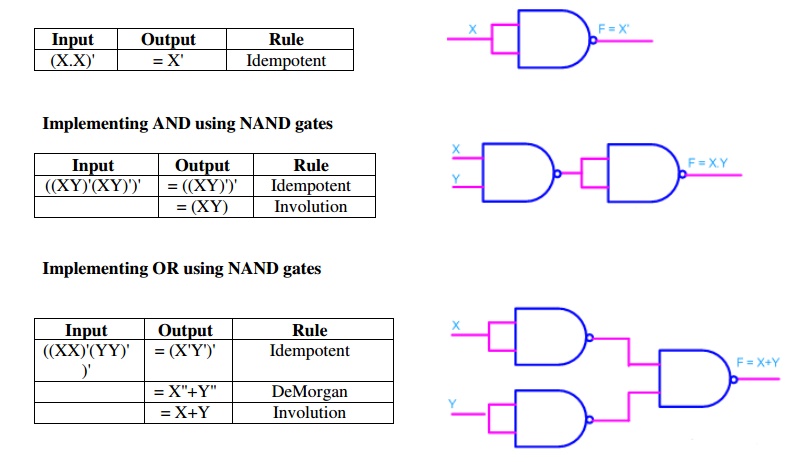
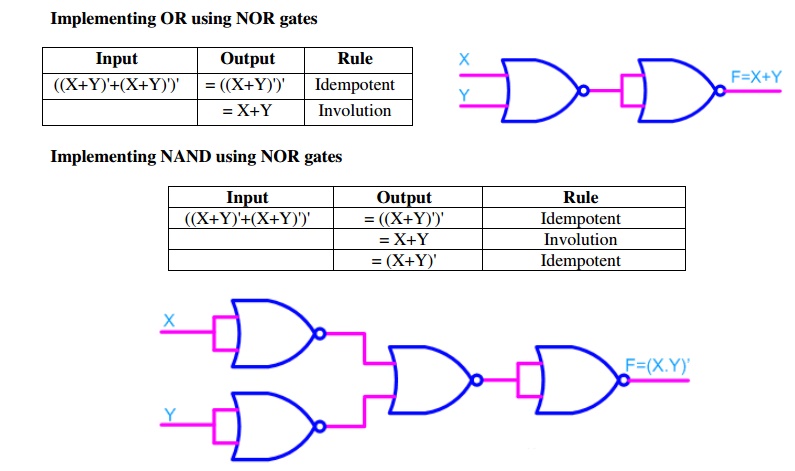
ü    Realization of logic function using NOR gates

Any logic function can be implemented using NOR gates. To achieve this, first the logic function has to be written in Product of Sum (POS) form. Once it is converted to POS, then it's very easy to implement using NOR gate. In other words any logic circuit with OR gates in first level and AND gates in second level can be converted into a NOR-NOR gate circuit.

Consider the following POS expression

F = (X+Y) . (Y+Z)

The above expression can be implemented with three OR gates in first stage and one AND gate in second stage as shown in figure.

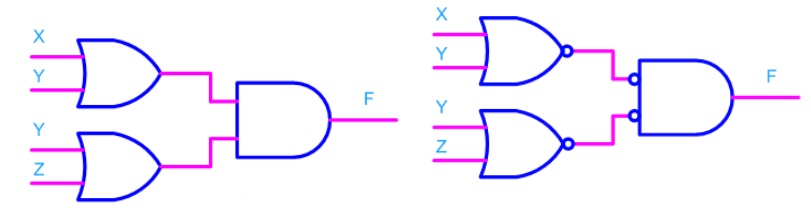
If bubble are introduced at the output of the OR gates and the inputs of AND gate, the above circuit becomes as shown in figure.

Now replace AND gate with input bubble with the NOR gate. Now we have circuit which is fully implemented with just NOR gates.

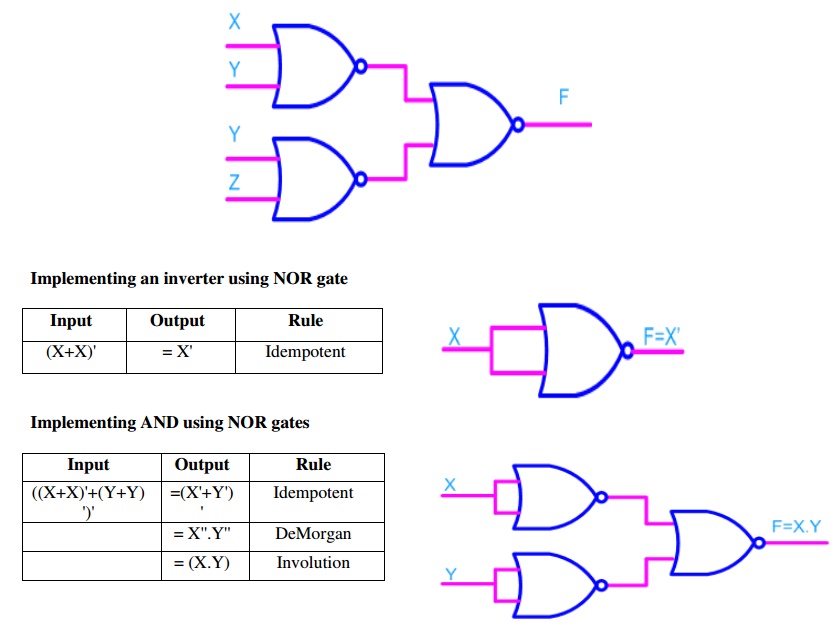
Minimization Technique

The primary objective of all simplification procedures is to obtain an expression that has the minimum number of terms. Obtaining an expression with the minimum number of literals is usually the secondary objective. If there is more than one possible solution with the same number of terms, the one having the minimum number of literals is the choice.

There are several methods for simplification of Boolean logic expressions. The process is usually called logic minimization and the goal is to form a result which is efficient. Two methods we will discuss are algebraic minimization and Karnaugh maps. For very complicated problems the former method can be done using special software analysis programs. Karnaugh maps are also limited to problems with up to 4 binary inputs. The Quine–McCluskey tabular method is used for more than 4 binary inputs.

Ref: 1)  A.P  Godse  &  D.A  Godse  “Digital  Electronics”,  Technical  publications,  Pune,  Revised edition, 2008. Pg.No:3.78

2)  Morris  Mano  M.  and  Michael  D.  Ciletti,  “Digital  Design”,  IV  Edition,  Pearson  Edition 2008.Pg.No:89.