Karnaugh Maps

KARNAUGH MAPS

Maurice Karnaugh, a telecommunications engineer, developed the Karnaugh map at Bell Labs in 1953 while designing digital logic based telephone switching circuits. Karnaugh maps reduce logic functions more quickly and easily compared to Boolean algebra.

A Karnaugh  map provides a pictorial method of grouping together expressions with common  factors and  therefore eliminating unwanted variables. The Karnaugh map can also be described  as a special  arrangement of a truth table.

Construction of a Karnaugh Map

1.       Each square containing a ‗1‘ must be consideredstonce,at leaalthough it can be considered as often as desired.

2.       The objective should be to account for all the marked squares in the minimum number of groups.

3.       The number of squares in a group must always be a power of 2, i.e. groups can have 1, 2, 4_ 8, 16, squares.

4.       Each group should be as large as possible, which means that a square should not be accounted for by itself if it can be accounted for by a group of two squares; a group of two squares should not be made if the  involved squares can be included in a group of four squares and so on.  

5. 'Don‘t care‘ entries can        be used in accountinglof-squares1foralto make optimum groups. They are marked ‗X‘ in the rrespondingco          squares. It is, however, not necessary to account       for all  'don‘t  care‘ entries. Only such entries that can be used to advantage should be used.     

The diagram  below illustrates the correspondence between the Karnaugh map and the truth table  for the  general case of a two variable problem.

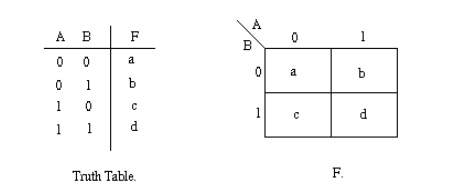
The values inside the squares are copied from the output column of the truth table, therefore there is one square in the map for every row in the truth table. Around the edge of the Karnaugh map are the values of the two input variable. A is along the top and B is down the left hand side. The diagram below explains this:

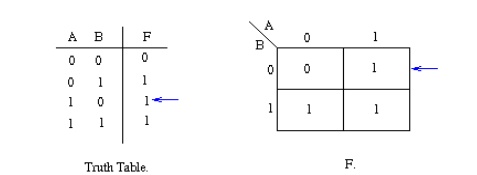
The values around the edge of the map can be thought of as coordinates. So as an example, the square on the top right hand corner of the map in the above diagram has coordinates A=1 and B=0. This square corresponds to the row in the truth table where A=1 and B=0 and F=1. Note that the value in the F column represents a particular function to which the Karnaugh map corresponds.

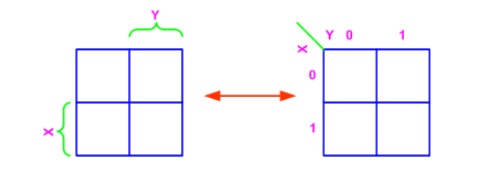
Two variable K-map

There are four minterms for two variables: hence, the map consists of four squares, one for each minterm. In any K-Map, each square represents a minterm. Adjacent squares always differ by just one literal (So that the unifying theorem may apply: X + X' = 1). For the 2-variable case (e.g.: variables X, Y), the map can be drawn as below. Two variable map is the one which has got only two variables as input.

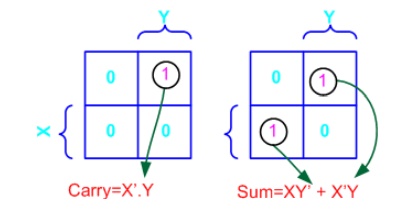
Example- Carry and Sum of a half adder

In this example we have the truth table as input, and we have two output functions. Generally we may have n output functions for m input variables. Since we have two output functions, we need to draw two k-maps (i.e. one for each function). Truth table of 1 bit adder is shown below. Draw the k-map for Carry and Sum as shown below.

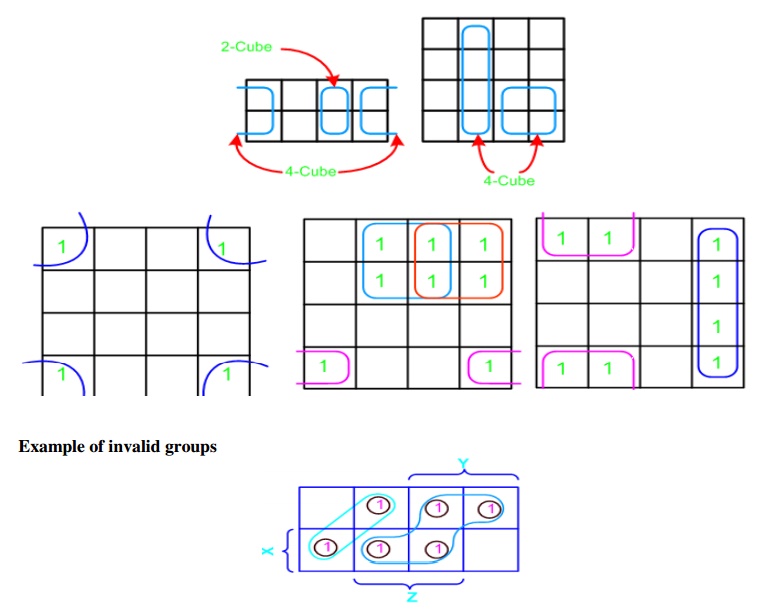
Grouping/Circling K-maps

The power of K-maps is in minimizing the terms, K-maps can be minimized with the help of grouping the terms to form single terms. When forming groups of squares, observe/consider the following:

•   Every square containing 1 must be considered at least once.

•     A square containing 1 can be included in as many groups as desired.

•     A group must be as large as possible.

•     If a square containing 1 cannot be placed in a group, then leave it out to include in final expression.

•     The number of squares in a group must be equal to 2 .i.e. 2,4,8,.

•     The map is considered to be folded or spherical, therefore squares at the end of a row or column are treated as adjacent squares.

•     The simplified logic expression obtained from a K-map is not always unique. Groupings can be made in different ways.

•     Before drawing a K-map the logic expression must be in canonical form.

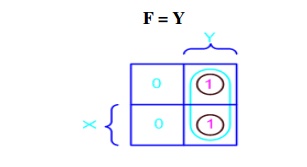
Example (1)- X'Y+XY: In this example we have the equation as input, and we have one output function. Draw the k-map for function F with marking 1 for X'Y and XY position. Now combine two 1's as shown in figure to form the single term. As you can see X and X' get canceled and only Y remains

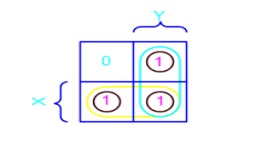
Example (2)- X'Y+XY+XY' :In this example we have the equation as input, and we have one output function. Draw the k-map for function F with marking 1 for X'Y, XY and XY position. Now combine two 1's as shown in figure to form the two single terms.

F = X + Y

3-Variable K-Map

There are 8 minterms for 3 variables (X, Y, Z). Therefore, there are 8 cells in a 3-variable K-map. One important thing to note is that K-maps follow the gray code sequence, not the binary one. Each cell in a 3-variable K-map has 3 adjacent neighbours. In general, each cell in an n-variable K-map has n adjacent neighbours.

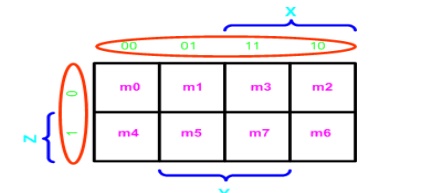
There is wrap-around in the K-map

•                     X'Y'Z' (m0) is adjacent to X'YZ' (m2)

•                     XY'Z' (m4) is adjacent to XYZ' (m6)

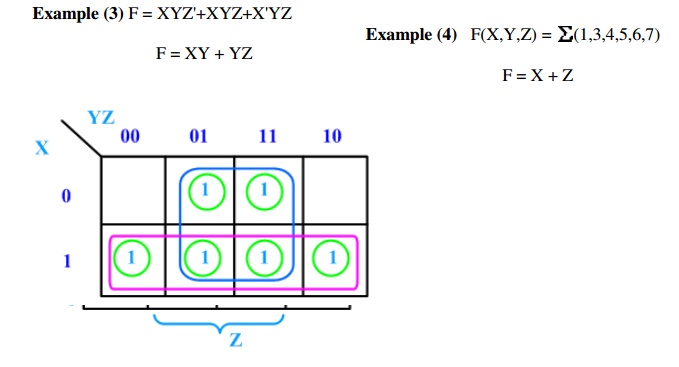
4-Variable K-Map: There are 16 cells in a 4-variable (W, X, Y, Z); K-map as shown in the figure below

Example (5) F(W,X,Y,Z) = (1,5,12,13)

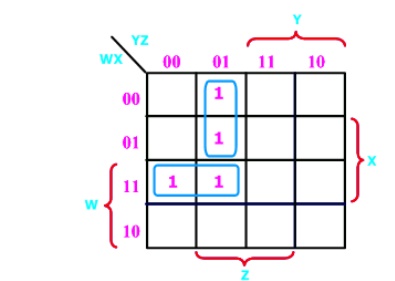
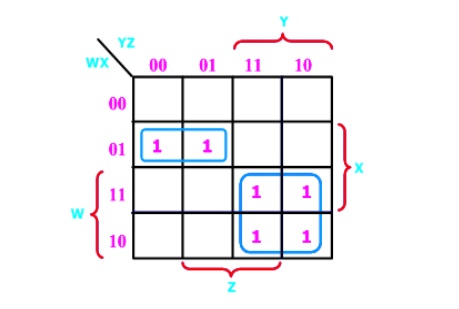
Example (6) F(W,X,Y,Z) = (4, 5, 10, 11, 14,15)

5-Variable K-Map: There are 32 cells in a 5-variable (V, W, X, Y, Z); K-map as shown in the figure below.

Ref: 1)  A.P  Godse  &  D.A  Godse  “Digital  Electronics”,  Technical  publications,  Pune,  Revised edition, 2008. Pg.No:2.25-2.70

2)  Morris  Mano  M.  and  Michael  D.  Ciletti,  “Digital  Design”,  IV  Edition,  Pearson  Education Pg.No:70.