Review of Number Systems

REVIEW OF NUMBER SYSTEMS

Many number systems are in use in digital technology. The most common are the decimal, binary, octal, and hexadecimal systems. The decimal system is clearly the most familiar to us because it is tools that we use every day.

Types of Number Systems are

1Decimal Number system                

2 Binary Number system                 

3 Octal Number system          

4 Hexadecimal Number system                 

                   Fig: Types of Number Systems      

          DECIMAL BINARY    OCTAL     HEXADECIMAL

          0        0000  0        0

          1        0001  1        1

          2        0010  2        2

          3        0011  3        3

          4        0100  4        4

          5        0101  5        5

          6        0110  6        6

          7        0111  7        7

          8        1000  10      8

          9        1001  11      9

          10      1010  12      A

          11      1011  13      B

          12      1100  14      C

          13      1101  15      D

          14      1110  16      E

          15      1111  17      F

Fig: Number system and their Base value

Decimal system: Decimal system is composed of 10 numerals or symbols. These 10 symbols are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Using these symbols as digits of a number, we can express any quantity. The decimal system is also called the base-10 system because it has 10 digits. Even though the decimal system has only 10 symbols, any number of any magnitude can be expressed by using our system of positional weighting.

Example:  3.14₁₀ , 52₁₀ ,1024₁₀

Binary System: In the binary system, there are only two symbols or possible digit values, 0 and 1. This base-2 system can be used to represent any quantity that can be represented in decimal or other base system.

In digital systems the information that is being processed is usually presented in binary form. Binary quantities can be represented by any device that has only two operating states or possible conditions. E.g.. A switch is only open or closed. We arbitrarily (as we define them) let an open switch represent binary 0 and a closed switch represent binary 1. Thus we can represent any binary number by using series of switches.

Binary 1: Any voltage between 2V to 5V Binary 0: Any voltage between 0V to 0.8V

Not used: Voltage between 0.8V to 2V in 5 Volt CMOS and TTL Logic, this may cause error in a digital circuit. Today's digital circuits works at 1.8 volts, so this statement may not hold true for all logic circuits.

Octal System: The octal number system has a base of eight, meaning that it has eight possible digits: 0,1,2,3,4,5,6,7.

Hexadecimal System: The hexadecimal system uses base 16. Thus, it has 16 possible digit symbols. It uses the digits 0 through 9 plus the letters A, B, C, D, E, and F as the 16 digit symbols.

Code Conversion

Converting from one code form to another code form is called code conversion, like converting from binary to decimal or converting from hexadecimal to decimal.

ü Binary-To-Decimal Conversion: Any binary number can be converted to its decimal equivalent simply by summing together the weights of the various positions in the binary number which contain a 1.

ü Decimal to binary Conversion:

There are 2 methods:

•        Reverse of Binary-To-Decimal Method

•        Repeat Division

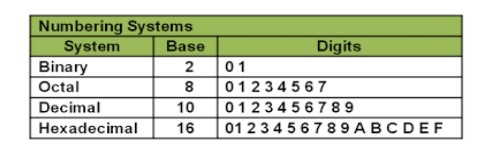
Reverse of Binary-To-Decimal Method

Repeat Division-Convert decimal to binary: This method uses repeated division by 2.

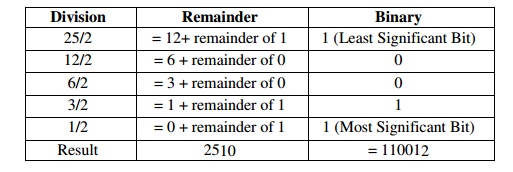
üBinary-To-Octal / Octal-To-Binary Conversion

Binary to octal

100 111 0102 = (100) (111) (010)2 = 4 7 28

üDecimal -To-Octal / Octal-To- Decimal Conversion

Decimal to octal

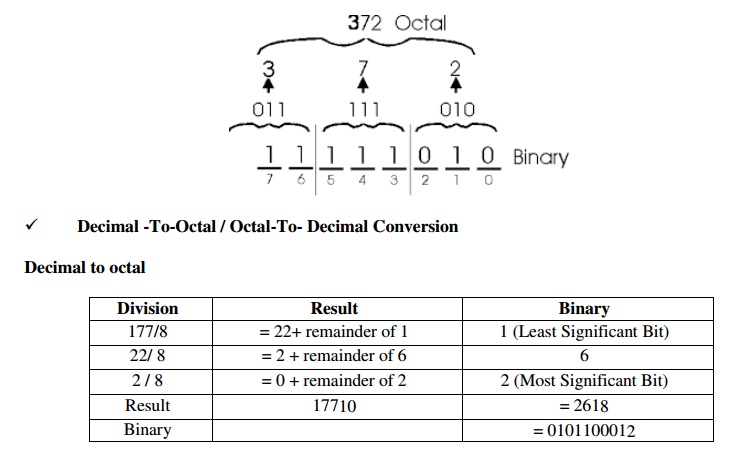
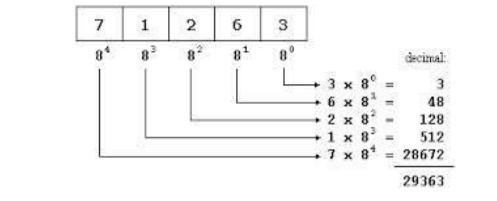
Octal to Decimal

ü Hexadecimal to Decimal/Decimal to Hexadecimal Conversion Decimal to Hexadecimal

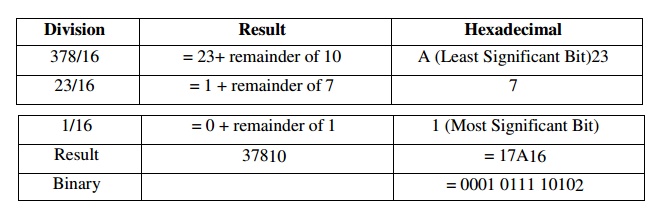
ü    Binary-To-Hexadecimal /Hexadecimal-To-Binary Conversion

Binary-To-Hexadecimal: 1011 0010 1111₂ = (1011) (0010) (1111)₂ = B 2 F₁₆

Hexadecimal to binary

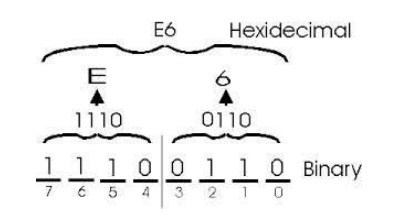
ü      Octal-To-Hexadecimal Hexadecimal-To-Octal Conversion

·                    Convert Octal (Hexadecimal) to Binary first.

·                    Regroup the binary number by three bits per group starting from LSB if Octal is required.

·                    Regroup the binary number by four bits per group starting from LSB if Hexadecimal is required.

Octal to Hexadecimal

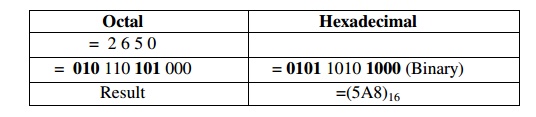
Hexadecimal  to octal

1’s and 2’s complement

Complements are used in digital computers to simplify the subtraction operation and for logical manipulation. There are TWO types of complements for each base-r system: the radix complement and the diminished radix complement. The first is referred to as the r's complement and the second as the (r - 1)'s complement, when the value of the base r is substituted in the name. The two types are referred to as the 2's complement and 1's complement for binary numbers and the 10’s complement a complement for decimal numbers.

The 1’s       complement of a binary number is the number that results when gewe allchan1’s to zeros and the zeros to ones.

The 2’s complement is the binary number that results when we add 1 to the 1’s complem It is used to represent negative numbers.

2’s complement=1’s complement+1

Ref: 1) A.P Godse & D.A Godse “Digital Electronics”, Technicalpublications, Pune, Revised third edition, 2008. Pg.No:1-17 

2) Morris  Mano  M.  and  Michael  D.  Ciletti,  “Digital  Design”,  IV  Edition,  Pearson  Edition 2008.Pg.No:1-8.