Basic Principles of Osmosis and Osmotic Pressure

Basic Principles of Osmosis and Osmotic Pressure

The basic principles of osmosis and osmotic pressure were presented earlier. Therefore, we review here only the most important aspects of these princi-ples as they apply to volume regulation.

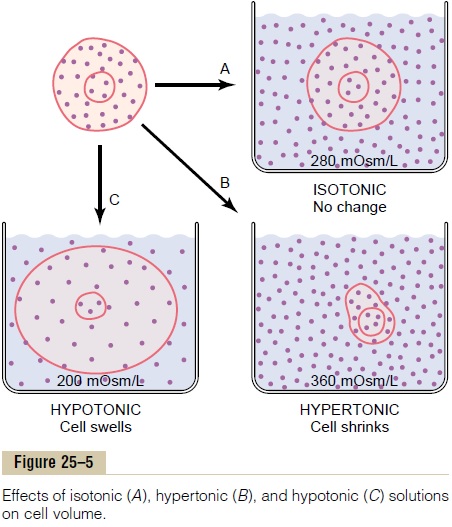
Osmosis is the net diffusion of water across a selec-tively permeable membrane from a region of high water concentration to one that has a lower water concentra-tion. When a solute is added to pure water, this reduces the concentration of water in the mixture. Thus, the higher the solute concentration in a solution, the lower the water concentration. Further, water diffuses from a region of low solute concentration (high water con-centration) to one with a high solute concentration (low water concentration).

Because cell membranes are relatively impermeable to most solutes but highly permeable to water (i.e., selectively permeable), whenever there is a higher concentration of solute on one side of the cell mem-brane, water diffuses across the membrane toward the region of higher solute concentration. Thus, if a solute such as sodium chloride is added to the extracellular fluid, water rapidly diffuses from the cells through the cell membranes into the extracellular fluid until the water concentration on both sides of the membrane becomes equal. Conversely, if a solute such as sodium chloride is removed from the extracellular fluid, water diffuses from the extracellular fluid through the cell membranes and into the cells. The rate of diffusion of water is called the rate of osmosis.

Relation Between Moles and Osmoles. Because the waterconcentration of a solution depends on the number of solute particles in the solution, a concentration term is needed to describe the total concentration of solute particles, regardless of their exact composition. The total number of particles in a solution is measured in osmoles. One osmole (osm) is equal to 1 mole (mol)(6.02 x 1023) of solute particles. Therefore, a solution containing 1 mole of glucose in each liter has a con-centration of 1 osm/L. If a molecule dissociates into two ions (giving two particles), such as sodium chlo-ride ionizing to give chloride and sodium ions, then a solution containing 1 mol/L will have an osmolar con-centration of 2 osm/L. Likewise, a solution that con-tains 1 mole of a molecule that dissociates into three ions, such as sodium sulfate (Na2SO4), will contain 3 osm/L. Thus, the term osmole refers to the number of osmotically active particles in a solution rather than to the molar concentration.

In general, the osmole is too large a unit for express-ing osmotic activity of solutes in the body fluids.

The term milliosmole (mOsm), which equals 1/1000 osmole, is commonly used.

Osmolality and Osmolarity. The osmolal concentration ofa solution is called osmolality when the concentration is expressed as osmoles per kilogram of water; it is called osmolarity when it is expressed as osmoles perliter of solution. In dilute solutions such as the bodyfluids, these two terms can be used almost synony-mously because the differences are small. In most cases, it is easier to express body fluid quantities in liters of fluid rather than in kilograms of water. There-fore, most of the calculations used clinically and the calculations expressed in the next several sections are based on osmolarities rather than osmolalities.

Osmotic Pressure. Osmosis of water molecules across aselectively permeable membrane can be opposed by applying a pressure in the direction opposite that of  the osmosis. The precise amount of pressure required to prevent the osmosis is called the osmotic pressure.Osmotic pressure, therefore, is an indirect measure-ment of the water and solute concentrations of a solu-tion. The higher the osmotic pressure of a solution, the lower the water concentration and the higher the solute concentration of the solution.

Relation Between Osmotic Pressure and Osmolarity. Theosmotic pressure of a solution is directly proportional to the concentration of osmotically active particles in that solution. This is true regardless of whether the solute is a large molecule or a small molecule. For example, one molecule of albumin with a molecular weight of 70,000 has the same osmotic effect as one molecule of glucose with a molecular weight of 180. One molecule of sodium chloride, however, has two osmotically active particles, Na+ and Cl–, and therefore has twice the osmotic effect of either an albumin mol-ecule or a glucose molecule. Thus, the osmotic pressure of a solution is proportional to its osmolarity, a measure of the concentration of solute particles.

Expressed mathematically, according to van’t Hoff ’s law, osmotic pressure (p) can be calculated as

π = CRT

where C is the concentration of solutes in osmoles per liter, R is the ideal gas constant, and T is the absolute temperature in degrees kelvin (273° + centigrade°). If π is expressed in millimeters of mercury (mm Hg), the unit of pressure commonly used for biological fluids, and T is normal body temperature (273° + 37° = 310° kelvin), the value of p calculates to be about 19,300 mm Hg for a solution having a concentration of 1 osm/L. This means that for a concentration of 1 mOsm/L, p is equal to 19.3 mm Hg. Thus, for each milliosmole concentration gradient across the cell membrane, 19.3 mm Hg osmotic pressure is exerted.

Calculation  of  the  Osmolarity  and  Osmotic  Pressure  of  a Solution. Using van’t Hoff’s law, one can calculate thepotential osmotic pressure of a solution, assuming that the cell membrane is impermeable to the solute.

For example, the osmotic pressure of a 0.9 per cent sodium chloride solution is calculated as follows: A 0.9 per cent solution means that there is 0.9 gram of sodium chloride per 100 milliliters of solution, or 9 g/L. Because the molecular weight of sodium chlo-ride is 58.5 g/mol, the molarity of the solution is 9 g/L divided by 58.5 g/mol, or about 0.154 mol/L. Because each molecule of sodium chloride is equal to 2 osmoles, the osmolarity of the solution is 0.154 x 2, or 0.308 osm/L. Therefore, the osmolarity of this solu-tion is 308 mOsm/L. The potential osmotic pressure of this solution would therefore be 308 mOsm/L x 19.3 mm Hg/mOsm/L, or 5944 mm Hg.

This calculation is only an approximation, because sodium and chloride ions do not behave entirely inde-pendently in solution because of interionic attraction between them. One can correct for these deviations from the predictions of van’t Hoff ’s law by using a correction factor called the osmotic coefficient. For sodium chloride, the osmotic coefficient is about 0.93. Therefore, the actual osmolarity of a 0.9 per cent sodium chloride solution is 308 x 0.93, or about 286 mOsm/L. For practical reasons, the osmotic coef-ficients of different solutes are sometimes neglected in determining the osmolarity and osmotic pressures of physiologic solutions.

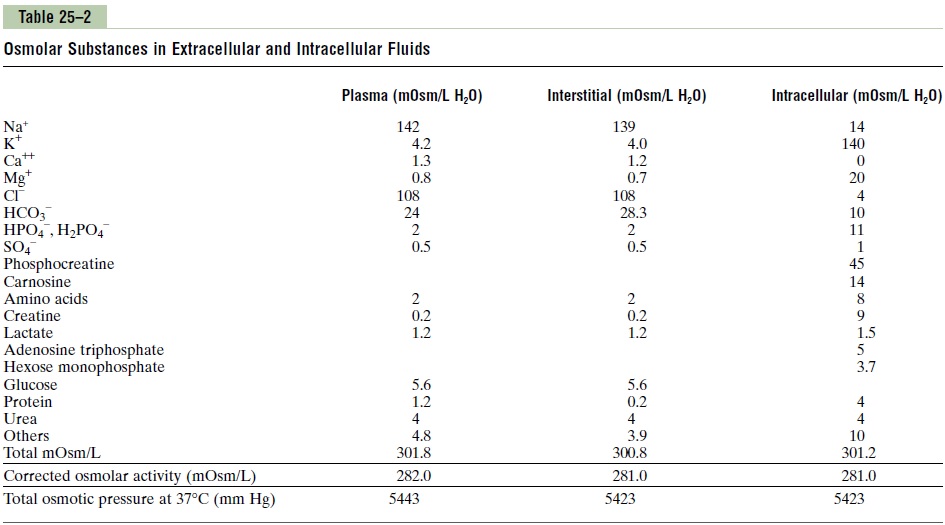
Osmolarity of the Body Fluids. Turning back to Table 25–2,note the approximate osmolarity of the various osmot-ically active substances in plasma, interstitial fluid, and intracellular fluid. Note that about 80 per cent of the total osmolarity of the interstitial fluid and plasma is due to sodium and chloride ions, whereas for intracel-lular fluid, almost half the osmolarity is due to potas-sium ions, and the remainder is divided among many other intracellular substances.

As shown in Table 25–2, the total osmolarity of each of the three compartments is about 300 mOsm/L, with the plasma being about 1 mOsm/L greater than that of the interstitial and intracellular fluids. The slight dif-ference between plasma and interstitial fluid is caused by the osmotic effects of the plasma proteins, which maintain about 20 mm Hg greater pressure in the cap-illaries than in the surrounding interstitial spaces.

Corrected Osmolar Activity of the Body Fluids. At thebottom of Table 25–2 are shown corrected osmolaractivities of plasma, interstitialfluid, and intracellularfluid. The reason for these corrections is that molecules and ions in solution exert interionic and intermolecu-lar attraction or repulsion from one solute molecule to the next, and these two effects can cause, respectively, a slight decrease or an increase in the osmotic “activ-ity” of the dissolved substance.

Total Osmotic Pressure Exerted by the Body Fluids. Table25–2 also shows the total osmotic pressure in millime-ters of mercury that would be exerted by each of the different fluids if it were placed on one side of the cell membrane with pure water on the other side. Note that this total pressure averages about 5443 mm Hg for plasma, which is 19.3 times the corrected osmolarity of 282 mOsm/L for plasma.