Algorithmic problem solving

ALGORITHMIC PROBLEM SOLVING:

Algorithmic problem solving is solving problem that require the formulation of an algorithm for the solution.

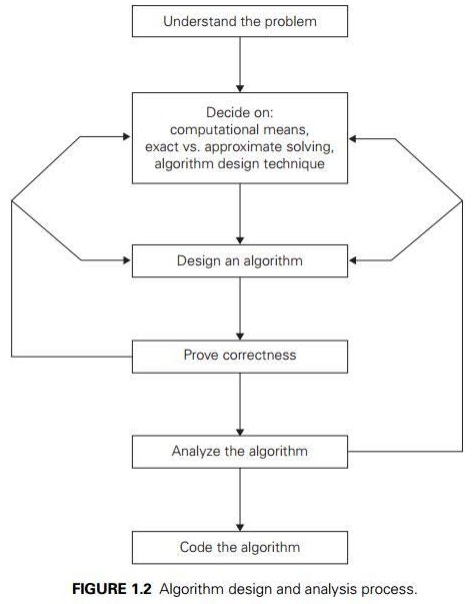
Understanding the Problem

v   It is the process of finding the input of the problem that the algorithm solves.

v   It is very important to specify exactly the set of inputs the algorithm needs to handle.

v   A correct algorithm is not one that works most of the time, but one that works correctly for all legitimate inputs.

Ascertaining the Capabilities of the Computational Device

v   If the instructions are executed one after another, it is called sequential algorithm.

v   If the instructions are executed concurrently, it is called parallel algorithm.

Choosing between Exact and Approximate Problem Solving

v   The next principal decision is to choose between solving the problem exactly or solving it approximately.

v   Based on this, the algorithms are classified as exact algorithm and approximation algorithm.

Deciding a data structure:

v   Data structure plays a vital role in designing and analysis the algorithms.

v   Some of the algorithm design techniques also depend on the structuring data specifying a problem’s instance

v   Algorithm+ Data structure=programs.

Algorithm Design Techniques

v   An algorithm design technique (or “strategy” or “paradigm”) is a general approach to solving problems algorithmically that is applicable to a variety of problems from different areas of computing.

v   Learning these techniques is of utmost importance for the following reasons.

v   First, they provide guidance for designing algorithms for new problems,

v   Second, algorithms are the cornerstone of computer science

Methods of Specifying an Algorithm

v   Pseudocode is a mixture of a natural language and programming language-like constructs. Pseudocode is usually more precise than natural language, and its usage often yields more succinct algorithm descriptions.

v   In the earlier days of computing, the dominant vehicle for specifying algorithms was a flowchart, a method of expressing an algorithm by a collection of connected geometric shapes containing descriptions of the algorithm’s steps.

v   Programming language can be fed into an electronic computer directly. Instead, it needs to be converted into a computer program written in a particular computer language. We can look at such a program as yet another way of specifying the algorithm, although it is preferable to consider it as the algorithm’s implementation.

Proving an Algorithm’s Correctness

v   Once an algorithm has been specified, you have to prove its correctness. That is, you have to prove that the algorithm yields a required result for every legitimate input in a finite amount of time.

v   A common technique for proving correctness is to use mathematical induction because an algorithm’s iterations provide a natural sequence of steps needed for such proofs.

v   It might be worth mentioning that although tracing the algorithm’s performance for a few specific inputs can be a very worthwhile activity, it cannot prove the algorithm’s correctness conclusively. But in order to show that an algorithm is incorrect, you need just one instance of its input for which the algorithm fails.

Analysing an Algorithm

1. Efficiency.

Time efficiency, indicating how fast the algorithm runs,

Space efficiency, indicating how much extra memory it uses.

2. simplicity.

v   An algorithm should be precisely defined and investigated with mathematical expressions.

v   Simpler algorithms are easier to understand and easier to program.

v   Simple algorithms usually contain fewer bugs.

Coding an Algorithm

v   Most algorithms are destined to be ultimately implemented as computer programs. Programming an algorithm presents both a peril and an opportunity.

v   A working program provides an additional opportunity in allowing an empirical analysis of the underlying algorithm. Such an analysis is based on timing the program on several inputs and then analysing the results obtained.