Chapter: Physics : Acoustics and Ultrasonics
Acoustics off buildings
Acoustics
of buildings
In day today life sound engineering plays a vital role in film industries, broadcasting of television signals and even in television signals. So a new field of science is developedwhich deals with the planning of a building or a hall with a view to provide best audiblesound to the audience and is called Acoustics of building. Therefore to provide a bestaudible sound in a building or hall a prime factor called Reverberation.
1
REVREBERATION
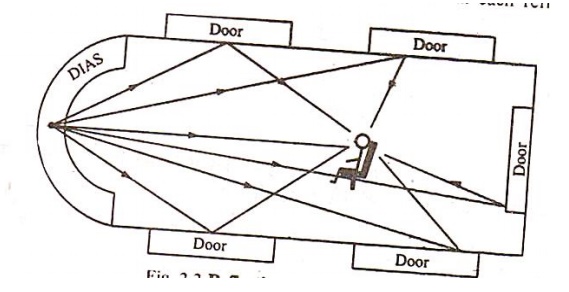
When a sound pulse is generated in a
hall, the sound wave travels towards all directionand are reflected back by the
walls, floors, doors, windows ceiling etc as shown in the figure.
So a sound wave has two to three hundred
repeated reflections, before it
becomes inaudible. Therefore, the
observer in the hall does not be able to hear a singlesharp sound instead a
"role of sound" of diminishing intensity (since part of energy is
lostat each reflection)
2
Reverberation time
The duration for which the sound persist
is termed as reverberation time
and is measured as the time interval
between the sound produced by the source
produced by the source and to the sound
wave until it dies.
Definition:
It is defined as the time taken for the
sound to fall below the minimum audibility
measured from the instant when the
source sound gets stopped.
In designing the auditorium, theatre,
conference halls etc, the reverberation time is
the key factor.
If the reverberation time is too large,
echoes are produced and if the reverberation
time is too short it becomes inaudible
by the observer and the sound is said to be dead.Therefore the reverberation
time should not be too large or too short rather it should havean optimum value.
In order to fix this optimum value
standard forumla is dervied by W.C.Sabine, who
defined the standard reverberation time
as the time taken for the sound to fall to one millionth of its original
intensity just before the source is cut off.

3
SABINES FORMULA FOR REVERBERRATION
The relation connecting the
reverberation time with the volume of the hall, the
area and the absorption coefficient is
known a s Sabine's Formula.
Sabine's developed the formula to
express the rise and fall of sound intensity by
the following assumptions.
I.
Distribution of sound energy is uniform
throughout the hall
II.
There is Interference between the sound
waves.
III.
The Absorption coefficient is
independent of sound intensity.
IV.
The Rate of emission of sound energy
from the source is constant.
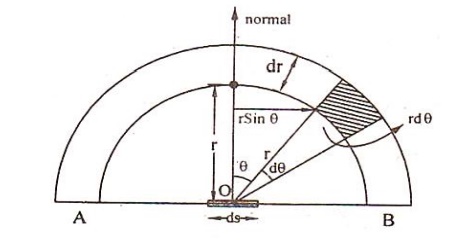
Let us consider a small element ‘ds’ on
a plane wall AB. Assume that the element ds receive the sound energy ‘E’.
Let us draw two concentric circles of
radii 'r' and r + dr from the center point 'O' of
ds. Consider a small shaded portion
lying in between the two semi circles drawn at an angle θ and θ+dθ, with the
normal to ds as shown in the figure.
Let 'dr' be th radial length and rdθ be the arc length
Area of shaded portion rd
If the whole figure is rotated about the
normal through an angle ‘dϕ’ as shown in the figure, then it is evident that
the area of the shaped portion travels through a small distance dx.
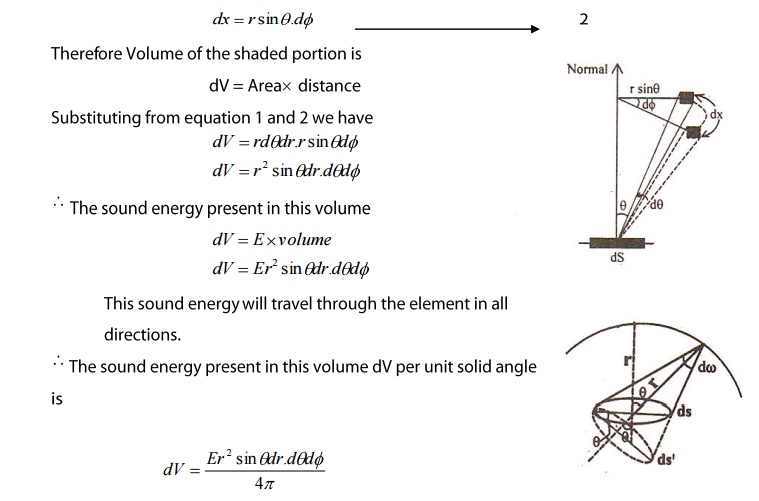

To find total energy received by the
element ‘ds’ per second, we have to integrate the equation 3 for the whole
volume lying within a distance ‘v’ is the Velocity of sound.
It is obvious from the geometry of the
figure that,


3.1
Growth and Decay of Sound Energy
If ‘P’ is the Power Output (i.e., the
rate of emission of sound energy from the source) then we can write
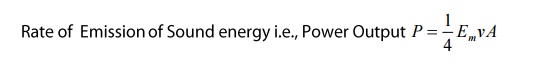
Here Em is the maximum energy
from the source (which has been emitted) that is maximum energy which is
incident on the wall

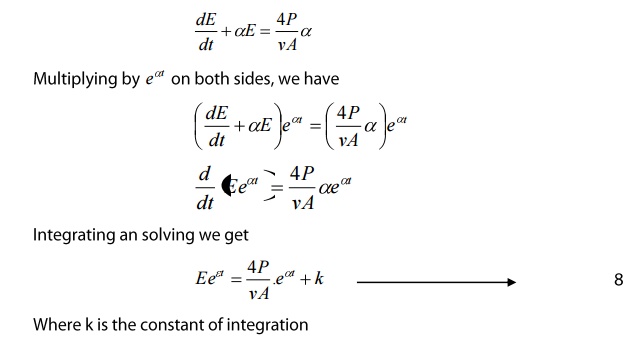
Where k is the constant of integration
3.2
Growth of Sound Energy
Let us evaluate for growth
Initially during the growth the boundary
conditions
Are at t=0 E=0
Thereore equation 8 becomes
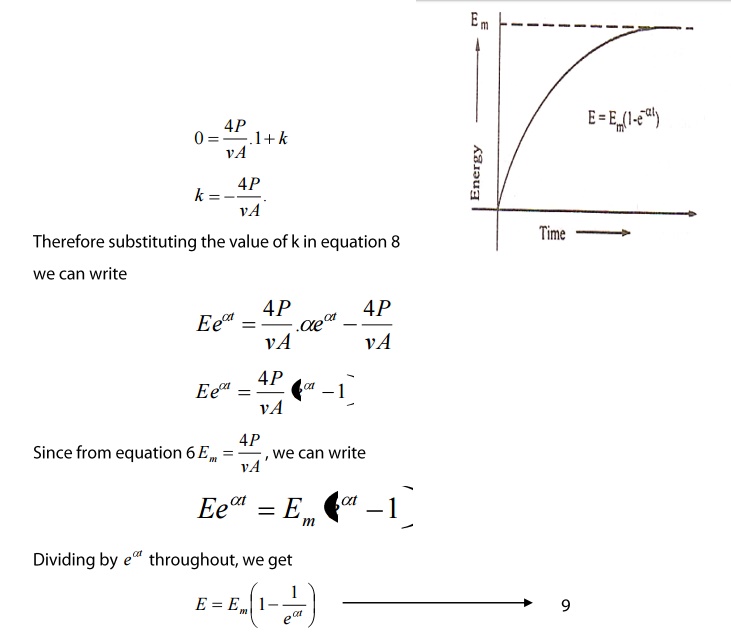
Where Em is the maximum sound
energy.
This expression gives the growth of
sound energy density ‘E’ with time ‘t’. The growth is along an exponential
curve as shown in the figure.
3.3
DECAY OF SOUND ENERGY
Let us irst evaluate k or decay.
Here the boundary conditions are at t=0;
E=Em
Initially the sound increases from E to
Em and now it is going to decay from Em. Therefore time is
considered as ‘0’ for E=Em. At E=Emv the sound energy from the source is cut off.
Therefore rate of emission of sound energy from the source=0 i.e., P=0
Therefore from equation 8 we can write

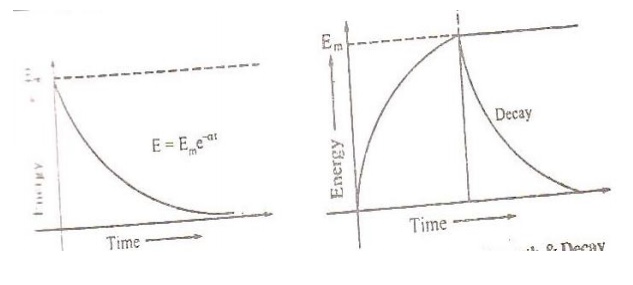
Equation 10 gives the decay of sound
energy density with time ‘t’ even after the source is cut off. It is
exponentially depressing function from maximum energy(Em) as shown. The growth
and decay of sound energy together is represented in the figure.
3.4
PROOF OF RREVEREBARTION TIME(T)
According to Sabine, the reverberation
time is defined as the time taken by a sound to fall to one millionth of its
initial value, when the source of sound is cut off.

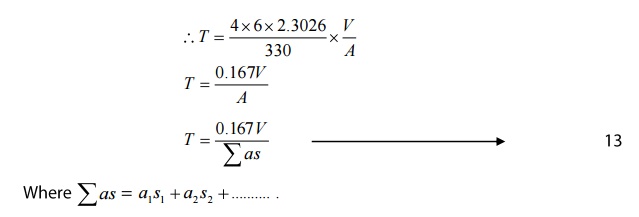
Equation 13 represents the Reverberation
time, which depends on the three factors viz,
i.
Volume of the hall(V)
ii.
Surface area(S)
iii.
Absorption coefficient(a) of the
materials kept inside the hall.
Among these three actors volume is
fixed. Therefore, the reverberation time can be optimized by either varying the
surface area of the reflecting surfaces or the absorption coefficient of the
materials used inside the hall.
Related Topics