Chapter: physics 11th 12th standard school college definition answer assignment examination viva question
Newton's rings : Experiment, Theory
Newton’s rings
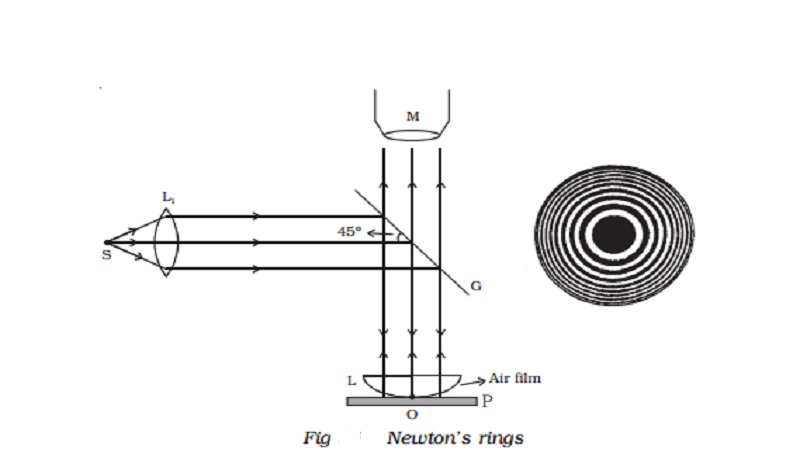
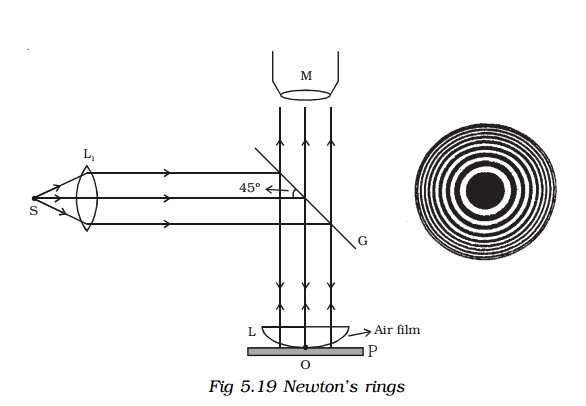
An important application of interference in thin films is the formation of Newton’s rings. When a plano convex lens of long focal length is placed over an optically plane glass plate, a thin air film with varying thickness is enclosed between them. The thickness of the air film is zero at the point of contact and gradually increases outwards from the point of contact. When the air film is illuminated by monochromatic light normally, alternate bright and dark concentric circular rings are formed with dark spot at the centre. These rings are known as Newton’s rings. When viewed with white light, the fringes are coloured (shown in the wrapper of the text book).
Experiment
Fig 5.19 shows an experimental arrangement for producing and observing Newton’s rings. A monochromatic source of light S is kept at the focus of a condensing lens L1. The parallel beam of light emerging from L1 falls on the glass plate G kept at 45o. The glass plate reflects a part of the incident light vertically downwards, normally on the thin air film, enclosed by the plano convex lens L and plane glass plate P. The reflected beam from the air film is viewed with a microscope. Alternate bright and dark circular rings with dark spot as centre is seen.
Theory
The formation of Newton’s rings can be explained on the basis of interference between waves which are partially reflected from the top and bottom surfaces of the air film. If t is the thickness of the air film at a point on the film, the refracted wavelet from the lens has to travel a distance t into the film and after reflection from the top surface of the glass plate, has to travel the same distance back to reach the point again.
Thus, it travels a total path 2t. One of the two reflections takes place at the surface of the denser medium and hence it introduces an additional phase change of π or an equivalent path difference λ/2 between two wavelets.
∴ The condition for brightness is, Path difference,

The thickness of the air film at the point of contact of lens L with glass plate P is zero. Hence, there is no path difference between the interfering waves. So, it should appear bright. But the wave reflected from the denser glass plate has suffered a phase change of π while the wave reflected at the spherical surface of the lens has not suffered any phase change. Hence the point O appears dark. Around the point of contact alternate bright and dark rings are formed.
Expression for the radius of the nth dark ring
Let us consider the vertical section SOP of the plano convex lens through its centre of curvature C, as shown in Fig 5.20. Let R be the radius of curvature of the plano convex lens and O be the point of contact of the lens with the plane surface. Let t be the thickness of the air film at S and P. Draw ST and PQ perpendiculars to the plane surface of the glass plate. Then ST = AO = PQ = t
Let rn be the radius of the nth dark ring which passes through the points S and P.
Then SA = AP = rn
If ON is the vertical diameter of the circle, then by the law of segments


Applications of Newtons rings
(i) Using the method of Newton’s rings, the wavelength of a given monochromatic source of light can be determined. The radius of nth dark ring and (n+m)th dark ring are given by

Related Topics