Magnetic Lorentz force

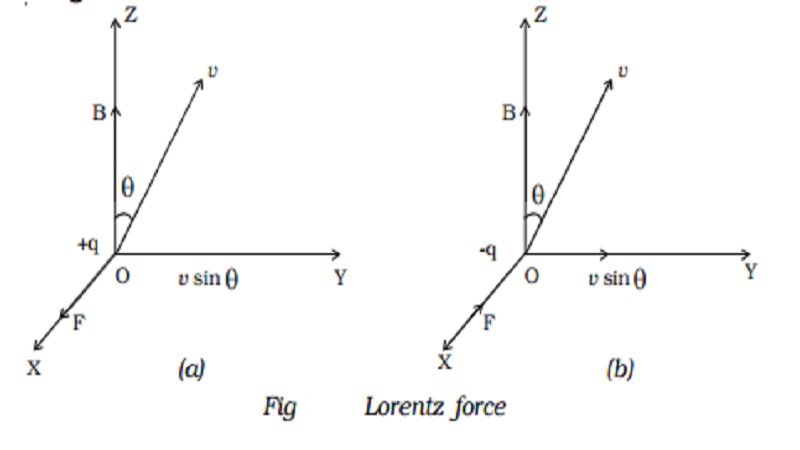
Magnetic Lorentz force

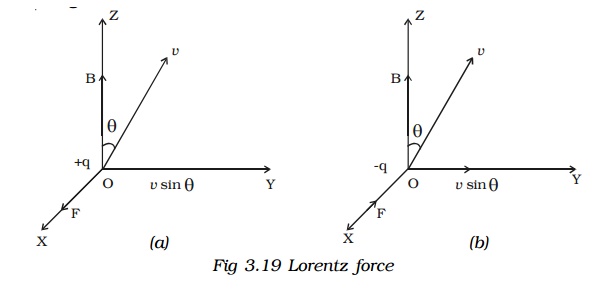
Let us consider a uniform magnetic field of induction B acting along the Z-axis. A particle of charge + q moves with a velocity vin YZ plane making an angle θ with the direction of the field (Fig 3.19a). Under the influence of the field, the particle experiences a force F.

H.A.Lorentz formulated the special features of the force F (Magnetic lorentz force) as under :

1.     the force F on the charge is zero, if the charge is at rest. (i.e) the moving charges alone are affected by the magnetic field.

2.     the force is zero, if the direction of motion of the charge is either parallel or anti-parallel to the field and the force is maximum, when the charge moves perpendicular to the field.

3. the force is proportional to the magnitude of the charge (q)

4.the force is proportional to the magnetic induction (B)

5.     the force is proportional to the speed of the charge (v)

6.     the direction of the force is oppositely directed for charges of opposite sign (Fig 3.19b).

All these results are combined in a single expression as

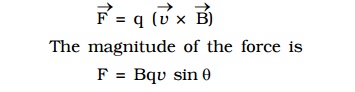
Since the force always acts perpendicular to the direction of motion of the charge, the force does not do any work.

In the presence of an electric field E and magnetic field B, the total force on a moving charged particle is

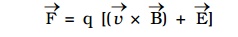
1. Motion of a charged particle in a uniform magnetic field.

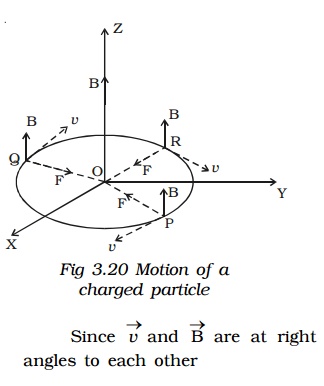
Let us consider a uniform magnetic field of induction B acting along the Z-axis. A particle of charge q and mass m moves in XY plane.

At a point P, the velocity of the particle is v. (Fig 3.20)

Since the force acts perpendicular to its velocity, the force does not do any work. So, the magnitude of the velocity remains constant and only its direction changes. The force F acting towards the point O acts as the centripetal force and makes the particle to move along a circular path. At points Q and R, the particle experiences force along QO and RO respectively.

F = Bqv sin 900 = Bqv

This magnetic lorentz force provides the necessary centripetal force.

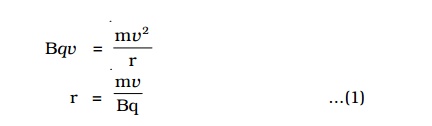
It is evident from this equation, that the radius of the circular path is proportional to (i) mass of the particle and (ii) velocity of the particle

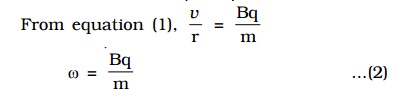
This equation gives the angular frequency of the particle inside the magnetic field.

Period of rotation of the particle,

From equations (2) and (3), it is evident that the angular frequency and period of rotation of the particle in the magnetic field do not depend upon (i) the velocity of the particle and (ii) radius of the circular path.