Algebraic Sensitivity Analysis-objective Function

Algebraic Sensitivity Analysis-objective Function

            In Previous Section  we used graphical sensitivity analysis to determine the conditions that will maintain the optimality of a two-variable LP solution. In this section, we extend these ideas to the general LP problem.

            Definition of Reduced Cost. To facilitate the explanation of the objective function sensitivity analysis, first we need to define reduced costs. In the TOYCO model (Example 3.6-2), the objective z-equation in the optimal tableau is

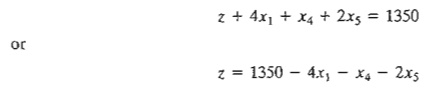
The optimal solution does not recommend the production of toy trains (x_l = 0). This recommendation is confirmed by the informatIon in the z-equation because each unit increase in Xl above its current zero level will decrease the value of z by $4 - namely, z = 1350 - 4 X (1) - 1 x (0) - 2 X (0) = $1346.

            We can think of the coefficient of x_l in the z-equation (= 4) as a unit cost be-cause it causes a reduction in the revenue z. But where does this "cost" come from? We know that xl has a unit revenue of $3 in the original model. We also know that each toy train consumes resources (operations time), which in turn incur cost. Thus, the "attractiveness" of x₁ from the standpoint of optimization depends on the relative values of the revenue per unit and the cost of the resources consumed by one unit. This relation-ship is formalized in the LP literature by defining the reduced cost as

To appreciate the significance of this definition, in the original TOYCO model the revenue per unit for toy trucks (= $2) is less than that for toy trains (= $3). Yet the optimal solution elects to manufacture toy trucks (x₂ = 100 units) and no toy trains (x₁ = 0). The reason for this (seemingly nonintuitive) result is that the unit cost of the resources used by toy trucks (i.e., operations time) is smaller than its unit price. The op-posite applies in the case of toy trains.

With the given definition of reduced cost we can now see that an unprofitable variable (such as Xl) can be made profitable in two ways:

1.     By increasing the unit revenue.

2.     By decreasing the unit cost of consumed resources.

In most real-life situations, the price per unit may not be a viable option because its value is dictated by market conditions. The real option then is to reduce the consump-tion of resources, perhaps by making the production process more efficient, as will be shown in Chapter 4.

Determination of the Optimality Ranges. We now turn our attention to determining the conditions that will keep an optimal solution unchanged. The presentation is based on the definition of reduced cost.

In the TOYCO model, let d₁ d₂, and d₃ represent the change in unit revenues for toy trucks, trains, and cars, respectively. The objective function then becomes

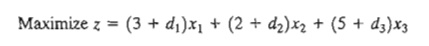
As we did for the right-hand side sensitivity analysis in Section 3.6.2, we will first deal with the general situation in which all the coefficients of the objective function are changed simultaneously and then specialize the results to the one-at-a-time case.

With the simultaneous changes, the z-row in the starting tableau appears as:

When we generate the simplex tableaus using the same sequence of entering and leaving variables in the original model (before the changes d _j are introduced), the op-timal iteration will appear as follows (convince yourself that this is indeed the case by carrying out the simplex row operations):

The new optimal tableau is exactly the same as in the original optimal tableau except that the reduced costs (z-equation coefficients) have changed. This means that changes in the objective-function coefficients can affect the optimality of the problem only.

You really do not need to carry out the row operation to compute the new reduced costs. An examination of the new z-row shows that the coefficients of d_i are taken directly from the constraint coefficients of the optimum tableau. A convenient way for computing the new reduced cost is to add a new top row and a new leftmost column to the optimum tableau, as shown by the shaded areas below. The entries in the top row are the change d _i associated with each variable. For the leftmost column, the entries are 1 in the z-row and the associated d_i in the row of each basic variable. Keep in mind that d _i = 0 for the slack variables.

Now, to compute the new reduced cost for any variable (or the value of z), multiply the elements of its column by the corresponding elements in the leftmost column, add them up, and subtract the top-row element from the sum. For example, for x_l, we have

Note that the application of these computations to the basic variables will always pro-duce a zero reduced cost, a proven theoretical result. Also, applying the same rule to the Solution column produces z = 1350 + 100d₂ + 230d₃.

Because we are dealing with a maximization problem, the current solution re-mains optimal so long as the new reduced costs (z-equation coefficients) remain non-negative for all the nonbasic variables. We thus have the following optimality conditions corresponding to nonbasic x₁ x₄, and x₅

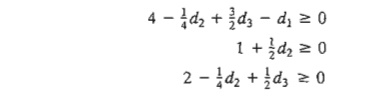
These conditions must be satisfied simultaneously to maintain the optimality of the current optimum.

To illustrate the use of these conditions, suppose that the objective function of TOYCO is changed from

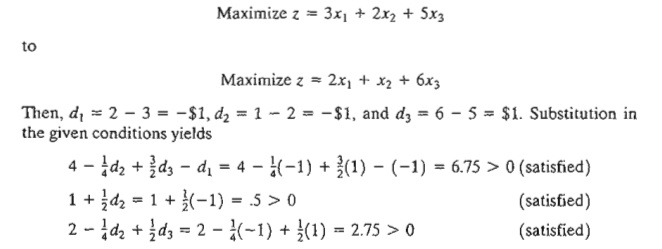
The results show that the proposed changes will keep the current solution (x₁  = 0,     x₂ = 100, x₃ = 230) optimal. Hence no further calculations are needed, except that the objective value will change to z = 1350 + 100d₂ + 230d₃ = 1350 + 100 X -1 + 230 X 1 = $1480. If any of the conditions is not satisfied, a new solution must be de-termined (see Chapter 4).

The discussion so far has dealt with the maximization case. The only difference in the minimization case is that the reduced costs (z-equations coefficients) must be ≤ 0 to maintain optimality.

The general optimality conditions can be used to determine the special case where the changes d _j occur one at a time instead of simultaneously. This analysis is equivalent to considering the following three cases:

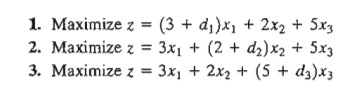
The individual conditions can be accounted for as special cases of the simultaneous case.

This condition assumes that the unit revenues for toy trains and toy cars remain fixed at $3 and $5, respectively.

The allowable range ($0, $10) indicates that the unit revenue of toy trucks (vari-able xz) can be as low as $0 or as high as $10 without changing the current optimum, x₁ = 0, x₂ = 100, x₃ = 230. The total revenue will change to 1350 + 100d₂, however.

It is important to notice that the changes d₁, d₂, and d₃ may be within their allow-able individual ranges without satisfying the simultaneous conditions, and vice versa. For example, consider

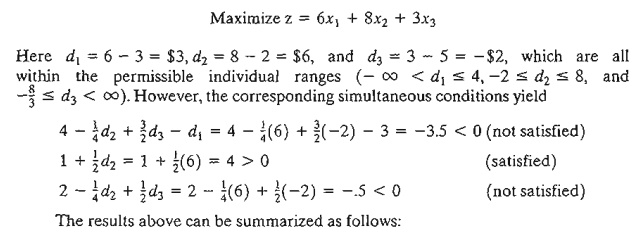
1.The optimal values of the variables remain unchanged so long as the changes d_j , j = 1, 2, ... , n, in the objective function coefficients satisfy all the optimality conditions when the changes are simultaneous or fall within the optimality ranges when a change is made individually_

2. For other situations where the simultaneous optimality conditions are not satisfied or the individual feasibility ranges are violated, the recourse is to either re-solve the problem with the new values of d_j or apply the post-optimal analysis presented in Chapter 4.

PROBLEM SET 3.60

1. In the TOYCO model, determine if the current solution will change in each of the following cases:

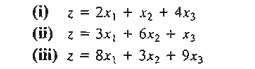
*2. B&K grocery store sells three types of soft drinks: the brand names Al Cola and A2 Cola and the cheaper store brand BK Cola. The price per can for Al, A2, and BK are 80, 70, and 60 cents, respectively. On the average, the store sells no more than 500 cans of all colas a day. Although Al is a recognized brand name, customers tend to buy more A2 and BK because they are cheaper. It is estimated that at least 100 cans of Al are sold daily and that A2 and BK combined outsell Al by a margin of at least 4:2.

a.Show that the optimum solution does not call for selling the A3 brand.

b.By how much should the price per can of A3 be increased to be sold by B&K?

c.To be competitive with other stores, B&K decided to lower the price on all three types of cola by 5 cents per can. Recompute the reduced costs to determine if this promotion will change the current optimum solution.

3. Baba Furniture Company employs four carpenters for 10 days to assemble tables and chairs. It takes 2 person-hours to assemble a table and .5 person-hour to assemble a chair. Customers usually buy one table and four to six chairs. The prices are $135 per table and $50 per chair. The company operates one 8-hour shift a day.

a.     Determine the 10-day optimal production mix.

b.     If the present unit prices per table and chair are each reduced by 10%, use sensitivi-ty analysis to determine if the optimum solution obtained in (a) will change.

c.      If the present unit prices per table and chair are changed to $120 and $,25, will the solution in (a) change?

4. The Bank of Elkins is allocating a maximum of $200,000 for personal and car loans dur-ing the next month. The bank charges 14% for personal loans and 12% for car loans. Both types of loans are repaid at the end of a I-year period. Experience shows that about 3 % of personal loans and 2 % of car loans are not repaid. The bank usually allocates at least twice as much to car loans as to personal loans.

a.     Determine the optimal allocation of funds between the two loans and the net rate of return on all the loans.

b.     If the percentages of personal and car loans are changed to 4% and 3%, respectively, use sensitivity analysis to determine jf the optimum solution in (a) will change.

*5. Electra produces four types of electric motors, each on a separate assembly line. The re-spective capacities of the lines are 500, 500, 800, and 750 motors per day. Type 1 motor uses 8 units of a certain electronic component, type 2 motor uses 5 units, type 3 motor uses 4 units, and type 4 motor uses 6 units. The supplier of the component can provide 8000 pieces a day. The prices per motor for the respective types are $60, $40, $25, $30.

a)     Determine the optimum daily production mix.

b)    The present production schedule meets Electra's needs. However, because of competition, Electra may need to lower the price of type 2 motor. What is the most re-duction that can be effected without changing the present production schedule?

c)     Electra has decided to slash the price of all motor types by 25%. Use sensitivity analysis to determine if the optimum solution remains unchanged.

d)    Currently, type 4 motor is not produced. By how much should its price be increased to be induded in the production schedule?

6. Popeye Canning is contracted to receive daily 60,000 lb of ripe tomatoes at 7 cents per pound from which it produces canned tomato juice, tomato sauce, and tomato paste. The canned products are packaged in 24-can cases. A can of juice uses lib of fresh tomatoes, a can of sauce uses 3/4 lb, and a can of paste uses ½  lb. The company's daily share of the market is limited to 2000 cases of juice, 5000 cases of sauce, and 6000 cases of paste. The wholesale prices per case of juice, sauce, and paste are $21, $9, and $12, respectively.

a.     Develop an optimum daily production program for Popeye.

b.     If the price per case for juice and paste remains fixed as given in the problem, use sensitivity analysis to determine the unit price range Popeye should charge for a case of sauce to keep the optimum product mix unchanged.

7. Dean's Furniture Company assembles regular and deluxe kitchen cabinets from precut lumber. The regular cabinets are painted white, and the deluxe are varnished. Both paint-ing and varnishing are carried out in one department. The daily capacity of the assembly department is 200 regular cabinets and 150 deluxe. Varnishing a deluxe unit takes twice as much time as painting a regular one. If the painting/varnishing department is dedicat-ed to the deluxe units only, it can complete 180 units daily. The company estimates that the revenues per unit for the regular and deluxe cabinets are $100 and $140, respectively.

a.     Formulate the problem as a linear program and find the optimal production sched-ule per day.

b.     Suppose that competition dictates that the price per unit of each of regular and deluxe cabinets be reduced to $80. Use sensitivity analysis to determine whether or not the optimum solution in (a) remains unchanged.