Wedges with Constant Body Forces

Wedges with Constant Body Forces

Gravity loading of massive concrete, stone, and soil structures often produce the largest components of stress for which the designer must provide. For slopes, retaining walls, and geologic formations, body force may, in fact, be the only load. Seismic loading is often approximated by the assumption of a constant acceleration applied to the structure and even when the acceleration is not constant, the assumption of a constant peak value gives the engineer a worst-case estimate.

A solution can be obtained in polar coordinates, but is more clearly pre-sented in the Cartesian reference frame shown in Figure 8.10. Letting γ_x and γ_y be the body-force components due to gravity in the subscripted directions and K = tanβ, the stress function:

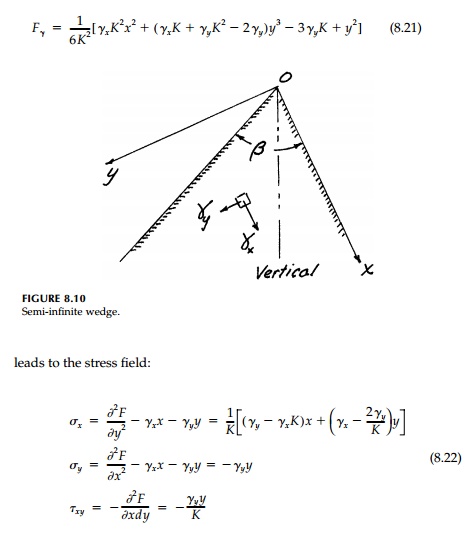
This is a wonderfully simple solution since it predicts a linear stress field. Therefore Ɐ²(σ_{x +} σ_y ) = 0 in a “trivial” fashion. We see, however, that the so-called “paradox of elasticity” we discovered in Section 8.2 again appears since for the half-space β = 180^o, K = 0, and the solution blows up. In fact, for wedges where β>90^o, this solution probably does not exist. Shown in Figure 8.11 are the analytic results for a 45o slope, which are certainly peculiar. The normal stress becomes larger and larger along the upper horizontal face as the distance from the crest, x, increases. This is nonsense. Yet as shown in Figure 8.11b, the seemingly unrealistic result certainly does give equilibrium and satisfy the boundary conditions on the exposed faces of the wedge.*

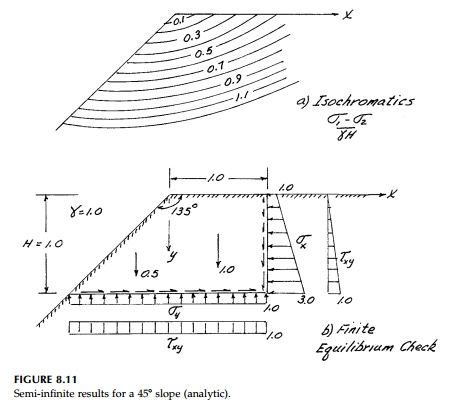
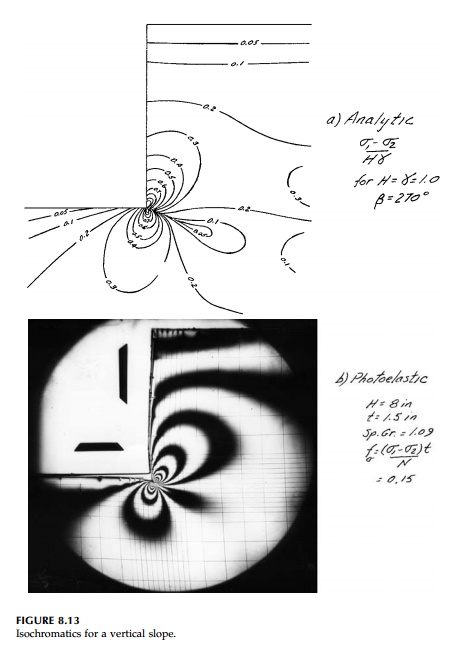
On the other hand, at β>= 90^o the analytic solution is perfectly reasonable and is used in the design of concrete gravity dams. Figure 8.12 shows a comparison of the analytic solution and experimental results for a gelatin model for a concrete dam shape in terms of isochromatics and isoclinics. The agreement is excellent. The same is true for a vertical cut (β= 90^o) shown in Figure 8.13.

It would appear then that this “paradox” is a problem with uniqueness, which, in retrospect, is not surprising. From our discussion in Chapter 4 of the Laplace equation Ɐ²(σ_x+ σ_y) = 0, we know that we can only guarantee a unique solution if we specify proper conditions over a closed boundary. Since no con-ditions are specified at r=   l arge in any of these wedge solutions, we must be

skeptical of results where the stress field does not either damp out as r �' or approaches the free field.

Example 8.3

A concrete gravity dam with a vertical upstream face is to be built so that, with a full reservoir, there will be no tension and an adequate factor of safety against crushing ( f'C=1125 psi = allowable compressive stress).

Knowing from our elasticity wedge solutions that the stresses will be distributed linearly over every horizontal cross-section, and assuming γ_w (water) = 62.4 lb/ft³, γ_c(concrete) = 150 lb/ft³, design the dam; i.e., determine: 

i.   the optimum angle 

ii. the maximum permissible height z_max  = H

Solve for the case of no horizontal acceleration and also for the case of a hor-izontal acceleration a_{x =} p k_h g with k_h = 0.3.

Comment on your results knowing that Shasta Dam in Northern California, (the highest gravity dam in the U.S.) is 580 feet high at an angle α = 36^o and was supposedly designed “at the limit” for such a concrete.

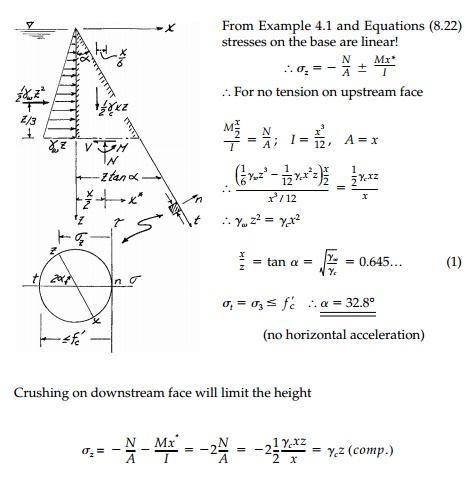
Shasta Dam is a good design. Actu-ally Shasta Dam looks more like the illustration at right. Concrete will take some tension and downward water force, Fw , will reduce or eliminate seis-mic tension at the heel. By bringing the downstream slope toward the vertical σt �' σz reducing crushing. Highest gravity dam is in Switzerland (no earthquakes) at z max > 900 ft. Reason- able since if σz = σy t, z max = fc′ /γc = 1080 ft with stronger concrete even greater heights are possible in non seismic zones.