Uniform Loading over a Finite Width

Uniform Loading over a Finite Width

Superposition of the solution for the half-space uniformly loaded along one axis gives us the solution for a strip of finite width as shown in Figure 8.6. The same result can also be obtained by integrating the result for a line load (Section 8.1) over the interval -b =< y =< b.

There are various ways to express the solution. In Cartesian coordinates:

If we consider principal stresses, the stress field is particularly simple:

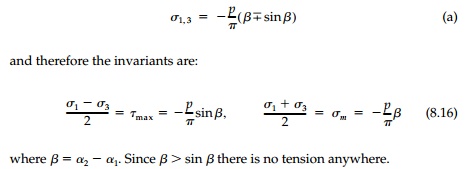
The stress trajectories are confocal ellipses and hyperbolas having the end points of the strip, F₁, and F₂, as foci as shown in Figure 8.6b. Both principal stresses have constant values along any circle passing through F₁ and F₂ with its center on the x axis (Figure 8.6c).

Moreover, the maximum shear stress has a maximum where

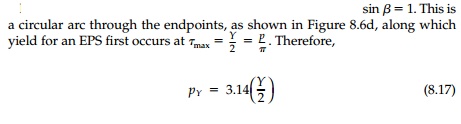
Although derived from solutions with ambiguity in the far field, this result is well behaved since every stress component damps out to the solution for a concentrated line load P = 2pb. We will see later that these results are useful

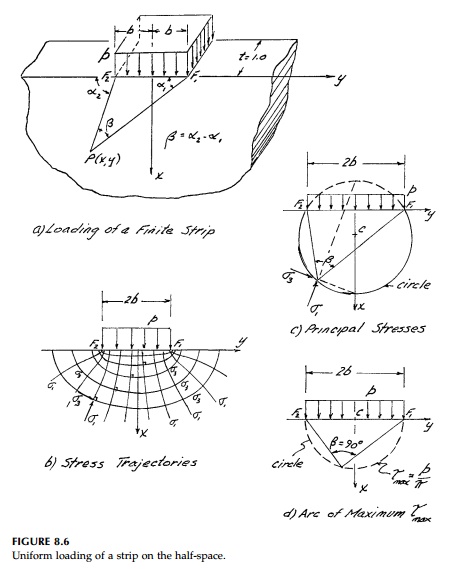
when we consider slip-line theory to calculate the collapse load for a uni-formly loaded strip.