Chapter: Civil : Principles of Solid Mechanics : Wedges and the Half-Space
Line Loads within the Half Space and Diametric Loading of a Circular Disk
Line Loads
within the Half Space
To complete our repertoire of 2D
solutions for the half-space, we need a solution for a vertical and horizontal
line load acting at some depth, d, below the surface of a semi-infinite
mass. Referring to Figure 8.8, the solution for plane strain*


This solution is again very useful for
numerical analysis. It is important to recognize that Poisson’s ratio now
appears in what would seem to be a two-dimensional problem. This is due to the
displacement conditions in the far field which we hypothesize is probably the
cause of difficulties with some of the previous wedge solutions. We will return
to this question of existence and uniqueness in the concluding section of this
chapter after the solution for constant body force loading of wedges is
presented.
Diametric Loading of a
Circular Disk
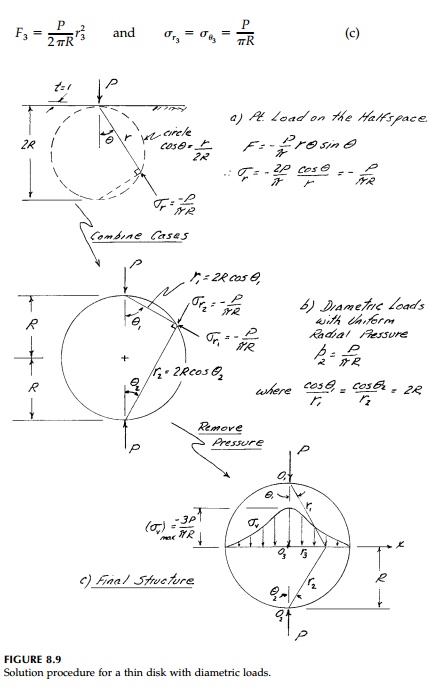
It is somewhat surprising that wedge
solutions can be applied to determine stresses in disks under
self-equilibrating loads. The simplest example is a disk with diametric,
concentrated loads as shown in Figure 8.9.*

We can then remove this pressure to
obtain the final result. More specifically, if we associate the stress function
F1 with the top load and F2 with the
bottom load then:
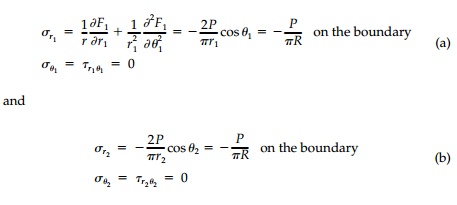
Finally, applying a uniform boundary
tension from the Lamé solution with the origin at the center of the disk

giving the stresses at any point as the
sum of three states, which must be transformed to a common orientation. For
example, at the center of the disk where
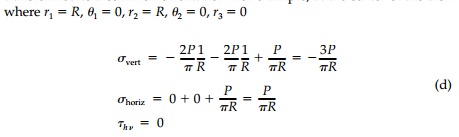
The distribution of vertical stress
along the horizontal diameter given by the expression
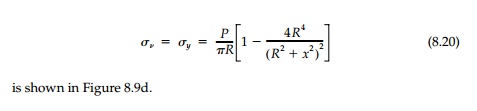
Related Topics