Uniform Loading Cases

Uniform Loading Cases

A similar paradox and a clue to its source and possible resolution can be seen clearly in the solution for a uniform (isotropic) loading on each face (Figure 8.4a) of a wedge. From the boundary condition that at any radius when,

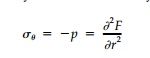
m must equal 2 and using only the symmetric terms

Clearly, since there is no singularity in the solution, its nonexistence for 2ϕ = 180^o introduces a more fundamental ambiguity. For wedge angles less than 90^o where there is no constraint on Eθ no matter what the radius, the isotropic field seems reasonable, but for 2ϕ > 90o , it seems suspect. Certainly equilib-rium, compatibility, and the stress boundary conditions are satisfied for any wedge angle, but there seems to be some added condition on deformations that precludes a simple isotropic field.

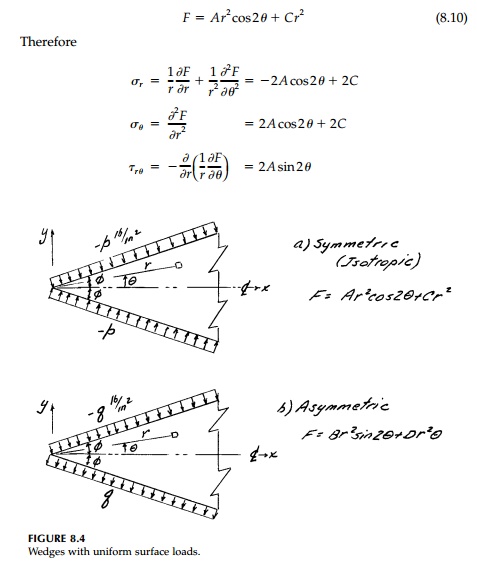
The same is true for the accepted solution for a wedge with uniform tension and compression on the faces (Figure 8.4b). Again, by similar reasoning, m = 2, the distribution of σ_r should be asymmetric and, therefore, we choose:

Again this solution cannot be correct in the far field for the half-space where the horizontal stress σ_y is a function of v. Moreover, the solution has the same singularity at 2ϕ= 257.4^o as in the case of a line moment at the apex [Equation (8.8)]. Again the denominator sin2ϕ = 2ϕcos2ϕ goes to zero and the solution blows up.

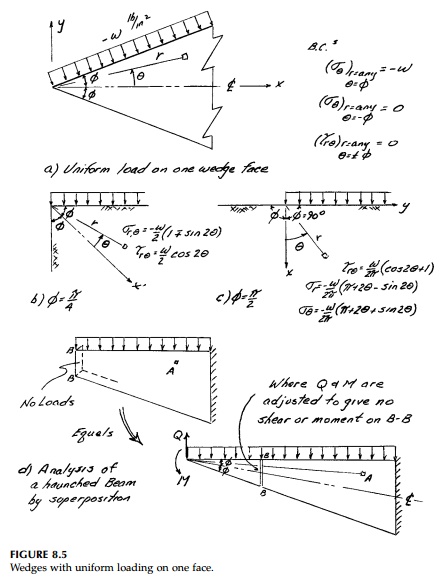
Finally, if we add the two previous cases together as in Figure 8.4 where w/2=p = q, this gives the solution for a wedge with a uniform load along the top surface (Figure 8.5).

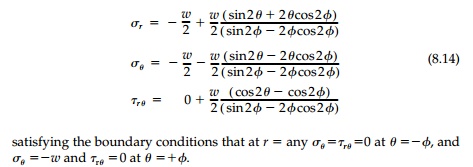
The special cases of a vertical cut, ϕ=45o , and the half-space are shown in Figure 8.5 b and c. Again in the far field under the load, the solution is sus-pect, but near the origin it gives sensible results. An example of how wedge solutions can be combined to give a solution for a haunched beam with uni-form loading is shown in Figure 8.5d. Other examples are given in the chap-ter problems.*

Example 8.2

A wedge is loaded by a uniform shearing traction, s, on its “upper” face as shown below. Determine the general stress function in terms of unknown coefficients A, B, C, and D.