Chapter: Civil : Principles of Solid Mechanics : Wedges and the Half-Space
Non uniform Loadings on the Half-Space
Non uniform
Loadings on the Half-Space
It has been mentioned that this result
for a uniform load on a finite width of the half-space could as easily be
obtained by integrating the point-load solu-tion. This is most easily seen in
terms of influence curves. Transforming the
Flamant solution [Equation (8.3)] for a
normal line load to Cartesian coordi-nates by Mohr’s Circle:
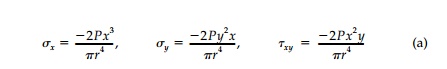
These components for a
unit load, P=1, as plotted in
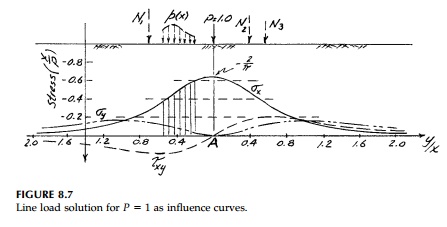
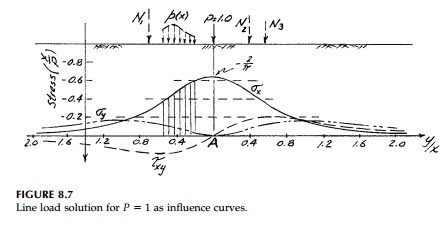
Figure 8.7 are influ-ence curves in that, by reciprocity, the stress at point A
(x0, 0) due to a load of magnitude N at point P (0, yo)
equals, at any depth, N times the stress at point B (x0y0)
due to P=1 at point 0 (0,0).
Suppose we want the stress at the depth of point A due to three normal forces N1, N2, and N3 on the surface as shown in Figure 8.7. The influence curve is located so the origin is directly above point A. The contribution to each stress component at A is then the magnitude of Ni times the ordinate of the corresponding influence curve under Ni. Therefore, to illustrate, σy at A would equal �'Ni ii or approximately N1(.3) N2(.47) N3(.35).
Similarly, by
superposition, the stresses under any nonuniform normal loading can be found to
any degree of accuracy desired by numerical inte-gration. The load p(x)
in Figure 8.7 is simply divided into increments, ∆x,
each of which is treated as a concentrated load pL∆xi
to be multiplied by the average ordinate of the influence curve under it. If p(x)
were constant as in the previous section, then σy would equal p
times the shaded area or approximately 0.5 pb.
Closed-form analytic solutions are
available for a number of nonuniform strip loadings (e.g., linear, parabolic,
etc.). From an engineering standpoint however, computation of stress from
influence lines given by point load solutions is perfectly adequate for design
and inherently more versatile. In fact, such influence lines, often called
Green’s Functions, are the fundamental building blocks of the boundary element
method for numerical analysis.
Another approach for nonconstant loading
is to use either a Fourier or polynomial series solution. Similarly, the
solutions for constant loading can be superimposed as step functions to
approximate any nonconstant distribu-tion. Some of these solutions for
nonuniform loading of the half-space are referred to in the chapter problems as
are the influence curves for tangential loading.
Related Topics