Wavelength of the Constituent Colours of a Composite Light Using Diffraction Grating and Spectrometer

WAVELENGTH OF THE CONSTITUENT COLOURS OF A COMPOSITE LIGHT USING DIFFRACTION GRATING AND SPECTROMETER

AIM

To find the wavelength of the constituent colours of a composite light using diffraction grating and spectrometer.

APPARATUS REQUIRED

Spectrometer, mercury vapour lamp, diffraction grating, grating table, and spirit level.

FORMULA

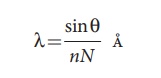
λ= sinθ/ nN Å

where,

λ → Wavelength of the constituent colours of a composite light (Å)

N → Number of lines per metre length of the given grating (No unit) (the value of N for the grating is given)

n → Order of the diffraction (No unit)

θ → Angle of diffraction (degree)

DIAGRAMS

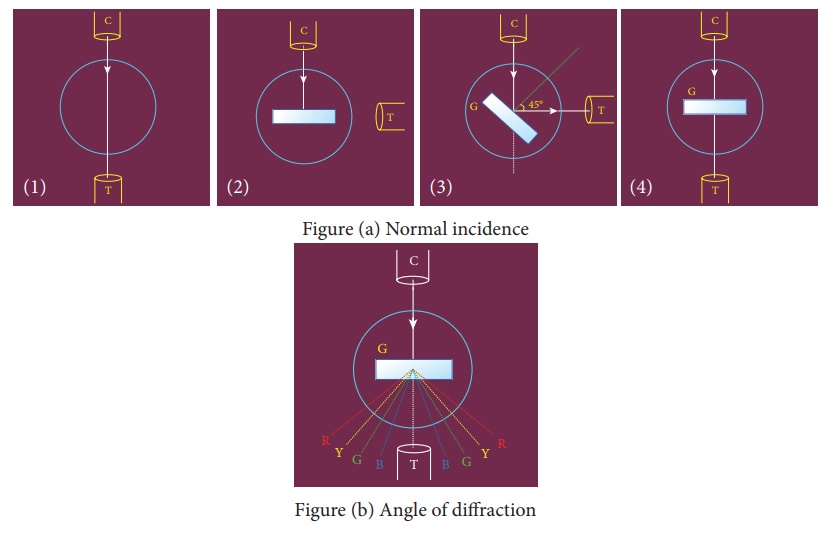
PROCEDURE

1) Initial adjustments of the spectrometer

·        Eye-piece: The eye-piece of the telescope is adjusted so that the cross-wires are seen clearly.

·        Slit: The slit of the collimator is adjusted such that it is very thin and vertical.

·        Base of the spectrometer: The base of the spectrometer is adjusted to be horizontal using leveling screws.

·        Telescope: The telescope is turned towards a distant object and is adjusted till the clear image of the distant object is seen. Now the telescope is adjusted to receive parallel rays.

·        Collimator: The telescope is brought in line with the collimator. Collimator is adjusted until a clear image of the slit is seen in the telescope. Now the collimator gives parallel rays.

·        Grating table: Using a spirit level, the grating table is adjusted to be horizontal with the three leveling screws provided in the grating table.

2) Adjustment of the grating for normal incidence

·        The slit is illuminated with a composite light (white light) from mercury vapour lamp.

·        The telescope is brought in line with the collimator. The vertical cross-wire is made to coin-cide with the image of the slit (Figure (a)1).

·        The vernier disc alone is rotated till the vernier scale reads 00 - 1800 and is fixed. This is the reading for the direct ray.

·        The telescope is then rotated (anti-clockwise) through an angle of 900 and fixed (Figure (a)2).

·        Now the plane transmission grating is mounted on the grating table.

·        The grating table alone is rotated so that the light reflected from the grating coincides with vertical cross-wire of the telescope. The reflected image is white in colour (Figure (a)3).

·        Now the vernier disc is released. The vernier disc along with grating table is rotated through an angle of 450 in the appropriate direction such that the light from the collimator is incident normally on the grating (Figure (a)4).

3) Determination of wave length of the constituent colours of the mercury spectrum

·        The telescope is released and is brought in line with the collimator to receive central direct image. This undispersed image is white in colour.

·        The diffracted images of the slit are observed on either side of the direct image.

·        The diffracted image consists of the prominent colours of mercury spectrum in increasing order of wavelength.

·        The telescope is turned to any one side (say left) of direct image to observe first order dif-fracted image.

·        The vertical cross-wire is made to coincide with the prominent spectral lines (violet, blue, yellow and red) and the readings of both vernier scales for each case are noted.

·        Now the telescope is rotated to the right side of the direct image and the first order image is observed.

·        The vertical cross-wire is made to coincide with the same prominent spectral lines and the readings of both vernier scales for each case are again noted.

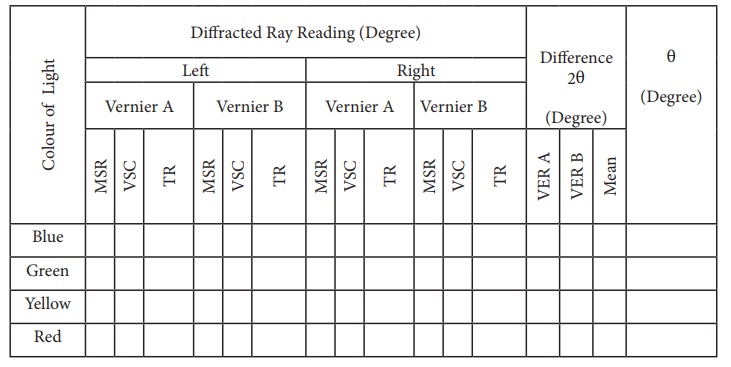
·        The readings are tabulated.

·        The difference between these two readings gives the value of 2θ for the particular spectral line.

·        The number of lines per metre length of the given grating N is noted from the grating.

·        From the values of N, n and θ, the wave length of the prominent colours of the mercury light is determined using the given formula.

OBSERVATION

To find the wave length of prominent colours of the mercury spectrum

CALCULATION

(i) For blue, λ= sinθ/ nN ,

(ii) For green, λ= sinθ / nN

(iii) For yellow, λ= sinθ / nN ,

(iv) For red, λ= sinθ / nN

RESULT

1. The wavelength of blue line = ---------------- m

2. The wavelength of green line = ------------------ m

3. The wavelength of yellow line = ---------------- m

4. The wavelength of red line = ---------------- m

Note:

i) Once initial adjustments are done, spectrometer should not be disturbed.

ii) Total reading TR = MSR + (VSC × LC)

Where

MSR → Main Scale Reading

VSC → Vernier Scale Coincidence

LC → Least count (= 1′)