Using Speculation to Break Dependencies

Using Speculation to Break Dependencies

In some instances, there is a clear potential dependency between different tasks. This dependency means it is impossible to use a traditional parallelization approach where the work is split between the two threads. Even in these situations, it can be possible to extract some parallelism at the expense of performing some unnecessary work. Consider the code shown in Listing 3.10.

Listing 3.10   Code with Potential for Speculative Execution

void doWork( int x, int y )

{

int value = longCalculation( x, y ); if (value > threshold)

{

return value + secondLongCalculation( x, y );

}

else

{

return value;

}

}

In this example, it is not known whether the second long calculation will be per-formed until the first one has completed. However, it would be possible to speculatively compute the value of the second long calculation at the same time as the first calculation is performed. Then depending on the return value, either discard the second value or use it. Listing 3.11 shows the resulting code parallelized using pseudoparallelization directives.

Listing 3.11  Speculatively Parallelized Code

void doWork(int x, int y)

{

int value1, value2;

#pragma start parallel region

{

#pragma perform parallel task

{

value1 = longCalculation( x, y );

}

#pragma perform parallel task

{

value2 = secondLongCalculation( x, y );

}

}

#pragma wait for parallel tasks to complete if (value1 > threshold)

{

return value1 + value2;

}

else

{

return value1;

}

}

The #pragma directives in the previous code are very similar to those that are actu-ally used in OpenMP, which we will discuss in Chapter 7, “OpenMP and Automatic Parallelization.” The first directive tells the compiler that the following block of code contains statements that will be executed in parallel. The two #pragma directives in the parallel region indicate the two tasks to be performed in parallel. A final directive indi-cates that the code cannot exit the parallel region until both tasks have completed.

Of course, it is important to consider whether the parallelization will slow perform-ance down more than it will improve performance. There are two key reasons why the parallel implementation could be slower than the serial code.

ⁿ   The overhead from performing the work and synchronizing after the work is close in magnitude to the time taken by the parallel code.

ⁿ   The second long calculation takes longer than the first long calculation, and the results of it are rarely used.

It is possible to put together an approximate model of this situation. Suppose the first calculation takes T1 seconds and the second calculation takes T2 seconds; also suppose that the probability that the second calculation is actually needed is P. Then the total runtime for the serial code would be T1 + P ∗ T2.

For the parallel code, assume that the calculations take the same time as they do in the serial case and the probability remains unchanged, but there is also an overhead from synchronization, S. Then the time taken by the parallel code is S + max (T1,T2).

Figure 3.22 shows the two situations.

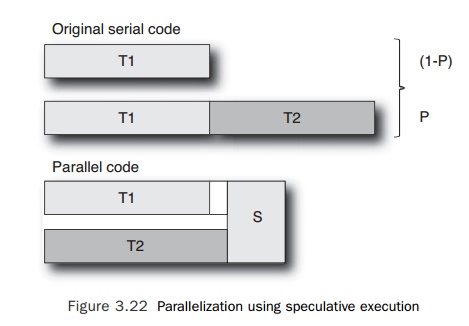
We can further deconstruct this to identify the constraints on the two situations where the parallel version is faster than the serial version:

ⁿ   If T1 > T2, then for the speculation to be profitable, S+T1 < T1+P∗T2, or

S < P∗T2. In other words, the synchronization cost needs to be less than the aver-age amount of time contributed by the second calculation. This makes sense if the second calculation is rarely performed, because then the additional overhead of synchronization needed to speculatively calculate it must be very small.

ⁿ If T2 > T1 (as shown in Figure 3.21), then for speculation to be profitable, S+T2 < T1+P∗T2 or P > (T2 +S -T1)/T2. This is a more complex result because the second task takes longer than the first task, so the speculation starts off with a longer runtime than the original serial code. Because T2 > T1, T2 + S -T1 is always >0. T2 + S -T1 represents the overhead introduced by parallelization. For the parallel code to be profitable, this has to be lower than the cost contributed by executing T2. Hence, the probability of executing T2 has to be greater than the ratio of the additional cost to the original cost. As the additional cost introduced by the parallel code gets closer to the cost of executing T2, then T2 needs to be executed increasingly frequently in order to make the parallelization profitable.

The previous approach is speculative execution, and the results are thrown away if they are not needed. There is also value speculation where execution is performed, speculating on the value of the input. Consider the code shown in Listing 3.12.

Listing 3.12  Code with Opportunity for Value Speculation

void doWork(int x, int y)

{

int value = longCalculation( x, y ); return secondLongCalculation( value );

}

In this instance, the second calculation depends on the value of the first calculation. If the value of the first calculation was predictable, then it might be profitable to specu-late on the value of the first calculation and perform the two calculations in parallel.

Listing 3.13 shows the code parallelized using value speculation and pseudoparallelization directives.

Listing 3.13   Parallelization Using Value Speculations

void doWork(int x, int y)

{

int value1, value2; static int last_value;

#pragma start parallel region

{

#pragma perform parallel task

{

value1 = longCalculation( x, y );

}

#pragma perform parallel task

{

value2 = secondLongCalculation( lastValue );

}

}

#pragma wait for parallel tasks to complete

if (value1 == lastvalue)

{

return value2;

}

else

{

lastValue = value1;

return secondLongCalculation( value1 );

}

}

The value calculation for this speculation is very similar to the calculation performed for the speculative execution example. Once again, assume that T1 and T2 represent the 

costs of the two routines. In this instance, P represents the probability that the specula-tion is incorrect. S represents the synchronization overheads. Figure 3.23 shows the costs of value speculation.

The original code takes T1+T2 seconds to complete. The parallel code takes max(T1,T2)+S+P∗T2. For the parallelization to be profitable, one of the following con-ditions needs to be true:

ⁿ   If T1 > T2, then for the speculation to be profitable, T1 + S + P∗T2 < T1 +T2. So, S < (1-P) ∗ T2. If the speculation is mostly correct, the synchronization costs just need to be less than the costs of performing T2. If the synchronization is often wrong, then the synchronization costs need to be much smaller than T2 since T2 will be frequently executed to correct the misspeculation.

ⁿ   If T2 > T1, then for the speculation to be profitable, T2 + S + P∗T2 < T1 +T2. So, S <T1 – P∗T2. The synchronization costs need to be less than the cost of T1 after the overhead of recomputing T2 is included.

As can be seen from the preceding discussion, speculative computation can lead to a performance gain but can also lead to a slowdown; hence, care needs to be taken in using it only where it is appropriate and likely to provide a performance gain.