How Synchronization Costs Reduce Scaling

How Synchronization Costs Reduce Scaling

Unfortunately, there are overhead costs associated with parallelizing applications. These are associated with making the code run in parallel, with managing all the threads, and with the communication between threads. You can find a more detailed discussion in Chapter 9, “Scaling on Multicore Systems.”

In the model discussed here, as with Amdahl’s law, we will ignore any costs intro-duced by the implementation of parallelization in the application and focus entirely on the costs of synchronization between the multiple threads. When there are multiple threads cooperating to solve a problem, there is a communication cost between all the threads. The communication might be the command for all the threads to start, or it might represent each thread notifying the main thread that it has completed its work.

We can denote this synchronization cost as some function F(N), since it will increase as the number of threads increases. In the best case, F(N) would be a constant, indicating that the cost of synchronization does not change as the number of threads increases. In the worst case, it could be linear or even exponential with the number threads. A fair estimate for the cost might be that it is proportional to the logarithm of the number of threads (F(N)=K*ln(N)); this is relatively easy to argue for since the logarithm represents the cost of communication if those threads communicated using a balanced tree. Taking this approximation, then the cost of scaling to N threads would be as follows:

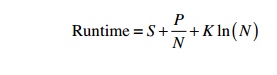
The value of K would be some constant that represents the communication latency between two threads together with the number of times a synchronization point is encountered (assuming that the number of synchronization points for a particular appli-cation and workload is a constant). K will be proportional to memory latency for those systems that communicate through memory, or perhaps cache latency if all the commu-nicating threads share a common level of cache. Figure 3.12 shows the curves resulting from an unrealistically large value for the constant K, demonstrating that at some thread count the performance gain over the serial case will start decreasing because of the syn-chronization costs.

It is relatively straightforward to calculate the point at which this will happen:

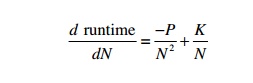
Solving this for N indicates that the minimal value for the runtime occurs when

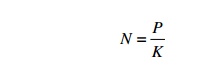
This tells us that the number of threads that a code can scale to is proportional to the ratio of the amount of work that can be parallelized and the cost of synchronization. So, the scaling of the application can be increased either by making more of the code run in parallel (increasing the value of P) or by reducing the synchronization costs (reducing the value of K). Alternatively, if the number of threads is held constant, then reducing the synchronization cost (making K smaller) will enable smaller sections of code to be made parallel (P can also be made smaller).

What makes this interesting is that a multicore processor will often have threads shar-ing data through a shared level of cache. The shared level of cache will have lower latency than if the two threads had to communicate through memory. Synchronization costs are usually proportional to the latency of the memory through which the threads communicate, so communication through a shared level of cache will result in much lower synchronization costs. This means that multicore processors have the opportunity to be used for either parallelizing regions of code where the synchronization costs were previously prohibitive or, alternatively, scaling the existing code to higher thread counts than were previously possible.

So far, this chapter has discussed the expectations that a developer should have when scaling their code to multiple threads. However, a bigger issue is how to identify work that can be completed in parallel, as well as the patterns to use to perform this work. The next section discusses common parallelization patterns and how to identify when to use them.