Unit Digit of Numbers in Exponential Form

Unit Digit of Numbers in Exponential Form

Manipulating with exponent is very interesting and funny too.

We know that 9³ = 9 × 9 × 9 = 729 , thus the unit digit (the last number of expanded form) of 9³ is 9. Similarly, 4⁴ is 4 × 4 × 4 × 4 = 256 . Thus the unit digit of 4⁴ is 6.

Can you guess the unit digit of 230¹¹⁶ , 181⁴⁷ , 55⁴ , 56²⁰ and 9²⁹ ?

It is very difficult to find by expanding the exponential form. But, we can try to tell the unit digit by observing some patterns.

Look at the following number pattern.

10³ = 10 ×10 ×10 = 1000

10⁴ = 10 ×10 ×10 ×10 = 10000

10⁵ = 10 ×10 ×10 ×10 ×10 = 100000

Thus, multiplying 10 by itself several times, we always get the unit digit as 0. In other words, 10 raised to the power of any number has the unit digit 0. That is, the unit digit of 10^x is always 0, for any positive integer x.

This is also true when the base is multiples of 10. Consider,

40² = (4 ×10)² = 4² ×10²

      =16 ×100 = 1600

Similarly, 230¹¹⁶ = (23 ×10)¹¹⁶ = 23¹¹⁶ ×10¹¹⁶

Thus, the unit digit of 230¹¹⁶ is 0.

Now, observe that,

1⁵ =1×1×1×1×1=1

1⁶ =1×1×1×1×1×1=1

We learnt to expand 11 as 10+1.

So,( 10 +1)² =11² =11×11 = 121

Similarly, 131=130 +1= (13×10)+1

[ (13 ×10) +1 ]² = 131² = 131 ×131 = 17161

Hence, if the exponential number is in the form 1^x or [(multiple of 10) +1]^x, then the unit digit is always 1, where x is a positive integer.

Therefore, the unit digit of 181⁴⁷ is 1.

Similarly, by observing the following patterns, we can conclude that the unit digit of number with base ending with 5 is 5 and number with base ending with 6 is 6.

5¹=5

5² =5×5=25

5³ =25×5=125

6¹=6

6² =6×6=36

6³ =36×6=216

Therefore, the unit digit of 55⁴ = ( 50 + 5)⁴ is 5 and the unit digit of 56²⁰ = ( 50 + 6)²⁰ is 6.

We conclude that, for the base number whose unit digits are 0,1,5 and 6 the unit digit of a number corresponding to any positive exponent remains unchanged.

Example 3.11

Find the unit digit of the following exponential numbers:

(i) 25²³

 (ii) 81¹⁰⁰

 (iii) 46³¹

Solution

(i) 25²³

Unit digit of base 25 is 5 and power is 23

Thus, the unit digit of 25²³ is 5.

(ii) 81¹⁰⁰

Unit digit of base 81 is 1 and power is 100

Thus, the unit digit of 81¹⁰⁰ is 1.

(iii) 46³¹

Unit digit of base 46 is 6 and power is 31

Thus, the unit digit of 46³¹ is 6.

Try these

Find the unit digit of the following exponential numbers:

(i) 106²¹ (ii) 25⁸ (iii) 31¹⁸ (iv) 20¹⁰

i) 106²¹

The unit digit of 106²¹ is 6.

ii) 25⁸

The unit digit of 25⁸ is 5.

iii) 31¹⁸

The unit digit of 31¹⁸ is 1.

iv) 20¹⁰

The unit digit of 20¹⁰ is 0.

Look into the following example. Observe the pattern of unit digit when the base is 4.

4¹=4 (odd power)                                       4²=4×4=16 (even power)

4³ = 4 × 4 × 4 = 16 × 4 = 64 (odd power)  4⁴ =64×4=256 (even power)

4⁵ = 256×4 =1024 (odd power)                 4⁶ = 1024×4=4096 (even power)

Note that for base ending with 4, the unit digit of the expanded form alternates between 4 and 6. Further we can notice when the power is odd its unit digit is 4 and when the power is even it is 6.

Similarly, when the base unit is 9,

9¹=9 (odd power)                                              9² =9×9=81 (even power)

9³ = 9 × 9 × 9 = 81 × 9 = 729 (odd power)        9⁴ =729×9=6561 (even power)

9⁵ = 6561× 9 = 59049 (odd power)                   9⁶ = 59049 × 9 = 531441 (even power)

Thus, for base ending with 9, the unit digit after the expansion is 9 for odd power and is 1 for even power.

As we have seen in the earlier case, this rule is applicable, when the base is in the form of [(multiple of 10)+4] or [(multiple of 10)+9].

For example consider, 24¹²

In this, unit digit of base 24 is 4 and power is 12 (even power).

Therefore, unit digit of 24¹² is 6.

Similarly consider, 89²¹

Here unit digit of base 89 is 9 and power is 21 (odd power).

Therefore, unit digit of 89²¹ is 9.

We conclude that, for base ending with 4, the unit digit of the expanded form is 4 for odd power and is 6 for even power. Similarly, for base ending with 9, the unit digit of the expanded form is 9 for odd power and is 1 for even power. Remember, 4 and 6 are complements of 10. Also, 9 and 1 are complements of 10.

Example 3.12

 Find the unit digit of the large numbers:

(i) 4⁷

(ii) 64¹⁰

Solution

(i) 4⁷

Unit digit of base 4 is 4 and power is 7 (odd power).

Therefore, unit digit of 4⁷ is 4.

(ii) 64¹⁰

Unit digit of base 64 is 4 and power is 10 (even power).

Therefore, unit digit of 64¹⁰ is 6.

Try these

Find the unit digit of the following exponential numbers:

(i) 64¹¹

Power 11 (odd power) so, the unit digit is 4.

(ii) 29¹⁸

Power 18 (even power) so, the unit digit is 1.

(iii) 79¹⁹

Power 19 (odd power) so, the unit digit is 9.

(iv) 104³²

Power 32 (even power) so, the unit digit is 6.

Example 3.13

 Find the unit digit of the large numbers: (i) 9¹² (ii) 49¹⁷

Solution

(i) 9¹²

Unit digit of base 9 is 9 and power is 12 (even power).

Therefore, unit digit of 9¹² is 1 .

(ii) 49¹⁷

Unit digit of base 49 is 9 and power is 17 (odd power).

Therefore, unit digit of 49¹⁷ is 9.

The following activity will help you to find the unit digits of exponent numbers whose base is ending with 2,3,7 and 8.

Activity

Observe the table given below. The numbers in first column, that is 2,3,7 and 8 denotes the unit digit of base of the given exponent number and the numbers in the first row, that is 1,2,3 and 0 stands for the remainder when power is divided by 4.

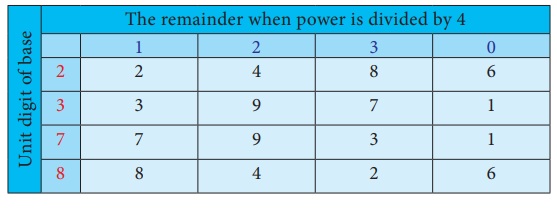
For example, consider 2⁶

Unit digit of base 2 is 2 and power is 6. When the power 6 is divided by 4, we get the remainder as 2.

From the table, we see that 2 and 2 corresponds to 4. Therefore, the unit digit of 2⁶ is 4. To verify, 2⁶ = 2 × 2 × 2 × 2 × 2 × 2 = 64 .

Similarly, consider 117²⁰

Unit digit of base 117 is 7 and power is 20. When the power 20 is divided by 4, we get the remainder as 0.

From the table, we see that 7 and 0 corresponds to 1. Therefore, the unit digit of 117²⁰ is 1.

Now, you can extend this activity for finding the unit digits of any exponent number whose base is ending with any of 2,3,7 or 8.