Exponents and Powers

Exponents and Powers

We can write large numbers in simplified form as given below.

For example, 16 = 8 × 2 = 4 × 2 × 2 = 2 × 2 × 2 × 2

Instead of writing the factor 2 repeatedly 4 times, we can simply write it as 2⁴. It can be read as 2 raised to the power of 4 or 2 to the power of 4 or simply 2 power 4.

This method of representing a number is called the exponential form. We say 2 is the base and 4 is the exponent.

Note

The exponent is usually written at the top right corner of the base and smaller in size when compared to the base.

Let us look at some more examples,

64 =4×4×4=4³              (base is 4 and exponent is 3)

Also, 64 =8×8=8²       (base is 8 and exponent is 2)

243 =3×3×3×3×3=3⁵ (base is 3 and exponent is 5)

125=5×5×5=5³              (base is 5 and exponent is 3)

Remember, when a number is expressed as a product of factors and when the factors are repeated, then it can be expressed in the exponential form. The repeated factor will be the base and the number of times the factor repeats will be its exponent.

We can extend this notation to negative integers also. For example,

−125 = (−5) × (−5) × (−5) = (−5)³ [base is ‘ −5 ’ and exponent is 3]

Hence, (−5)³ is the exponential form of −125 .

MATHEMATICS ALIVE - Algebra in Real Life

In a calculator, multiplication of two large numbers is displayed as 1.219326E17 which means 1.219326 × 10¹⁷ where, ‘E’ stands for exponent with base 10.

Numbers in Exponential Form

Now, we will see how to express numbers in exponential form.

Let us take any integer as ‘a’.

Then, a = a¹ [‘a power 1’]

a × a = a² [‘a power 2’ ; ‘a’ is multiplied by itself 2 times]

a × a × a = a³ [‘a power 3’ ; ‘a’ is multiplied by itself 3 times]

 :    :    :

 :    :    :

 a × a × a  = a³ (n times) = aⁿ [‘a power n’ ; ‘a’ multiplied by itself n times]

Thus we can generalize the exponential form as aⁿ, where the exponent is a positive integer (n > 0) .

Observe, the following examples.

100 = 10 ×10 = 10²

This can also be expressed as the product of two different bases with the same exponent as, 100=25×4=(5×5)×(2×2)=5² ×2²

We notice that 5 and 2 are the bases and 2 is the exponent.

In the same way, a × a × a × b × b = a ³ × b²

Consider, 35 = 7¹ × 5¹ , where there is no repetition of factors. Thus, usually 7¹×5¹ is represented as 7×5. So, when the power is 1 the exponent will not be explicitly mentioned.

Think

Note

1. The exponents 2 and 3 have special names ‘squared’ and ‘cubed’ respectively. For example, 4² is read as ‘four squared’ and 4³ is read as ‘four cubed’.

2. The other name of exponent is indices. Do you remember the word ‘indices’? In Class VI, we heard of this word while applying BIDMAS rule in simplification. For example,

6³ +4×3−5 =(6×6×6)+4×3−5[BIDMAS]

= 216 + (4×3) – 5 [BIDMAS]

= 216 +12–5 [BIDMAS]

= 228 – 5 [BIDMAS]

= 223

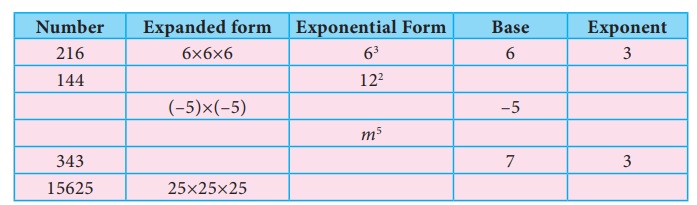
Try these

Observe and complete the following table. First one is done for you.

Example 3.1

Express 729 in exponential form.

Solution

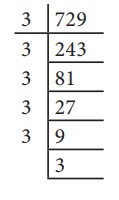
Dividing by 3, we get

729=3×3×3×3×3×3=3⁶

Also, 729 = 9 × 9 × 9 = 9³

Example 3.2

Express the following numbers in exponential form with the given base:

(i) 1000, base 10

(ii) 512, base 2

(iii) 243, base 3.

Solution

 (i) 1000 = 10 ×10 ×10 = 10³

 (ii) 512 =2×2×2×2×2×2×2×2×2=2⁹

 (iii) 243 =3×3×3×3×3=3⁵

Example 3.3

 Find the value of (i) 13² (ii) (−7)² (iii) (−4)³

Solution

Note

(–1)ⁿ = –1, if n is an odd natural number.

(–1)ⁿ = 1, if n is an even natural number.

 (i) 13² = 13 ×13 = 169

(ii) (−7)² = (−7) × (−7) = 49

(iii) (−4)³ = (−4) × (−4) × (−4)

               =16 × (−4) = −64

Think

Can you find two positive integers ‘a’ and ‘b’ such that a^b = b^a ? ( a ≠ b )

Example 3.4

Find the value of 2³ + 3²

Solution

2³ +3² =(2×2×2)+(3×3)

=8+9=17

Example 3.5

Which is greater 3⁴ or 4³ ?

Solution

3⁴ =3×3×3×3=81

4³ =4×4×4=64

81 > 64 gives 3⁴ > 4³

Therefore, 3⁴ is greater.

Example 3.6

Expand a ³b² and a ²b³. Are they equal ?

Solution

a ³b² = (a × a × a) × (b × b)

a ²b³ = (a × a) × (b × b × b)

Therefore, a ³b² ≠ a ²b³

Ancient Tamilians have used lot of greater numbers in their day-to-day life. Refer to Kanakkathikaram written by a saint Karinayanar who lived in Tamilnadu during 10th century. More interestingly, they fixed a unique name for every big number. For example, ‘Arpudham’ means Ten crores, ‘Padmam’ means 10¹⁴ , ‘Anantham’ means 10²⁹ and the word ‘Avviyatham’ denotes 10³⁵.

Pingalandai Nigandu Vaipaadu, an ancient Tamil Mathematics treatise, also confirms the usage of such big numbers. It is a book of multiplication table.