Exercise 3.4

Exercise 3.4

Miscellaneous Practice problems

1. 6²× 6^m = 6⁵, find the value of ‘m’.

6^2+m = 6⁵

Base are equal. So powers also equal.

2 + m =5

m = 5–2 = 3

m = 3

2. Find the unit digit of 124¹²⁸ × 126¹²⁴ .

Unit digit of base 124 is 4 and power is 128 (Even number).

So, the unit digit of 124¹²⁸ is 6.

Unit digit of base 126 is 6 and power is 124 (Even number).

So, the unit digit of 126¹²⁴ is 6.

6 × 6 = 36, Unit digit of 36 is 6.

So, Unit digit of 124¹²⁸ × 126¹²⁴ is 6.

3. Find the unit digit of the numeric expression: 16²³ + 71⁴⁸ + 59⁶¹

Unit digit of base 16 is 6 and power is 23 (Odd number).

So, the unit digit of 16²³ is 6.

Unit digit of base 71 is 1 and power is 48 (Even number).

So, the unit digit of 71⁴⁸ is 1.

Unit digit ofbase 59 is 9 and power is 61 (Odd number).

So, the unit digit of 59⁶¹ is 9. 

Adding Unit digits, 6+1+9 = 16, Unit digit of 16 is 6.

So, unit digit of 16²³ + 71⁴⁸ + 59⁶¹ is 6.

4. Find the value of  .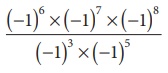

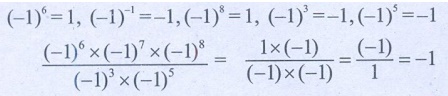
[ ( −1)⁶ × ( −1)⁷ × ( −1)⁸ ] / [ ( −1)³ × ( −1)⁵ ]

[ (–1)⁶ × (–1)⁷ × (–1)⁸ ] / [ (–1)³ × (–1)⁵ ]

(–1)⁶ = 1, (–1)^–1 = –1, (–1)⁸ = l, (–1)³ = –1, (–1)⁵ = –1

[ (–1)⁶ × (–1)⁷ × (–1)⁸  ] / [ (–1)³ × (–1)⁵ ] = [ 1 × (–1) ] / [ (–1) × (–1) ] = (–1) / 1 = –1

5. Identify the degree of the expression, 2a ³bc + 3a³b + 3a³c − 2a²b ² c²

Degree of 2a³bc is 5

Degree of 3a³b is 4

Degree of 3a³c is 4

Degree of 2a²b²c² is 6

The degree of the expression is 6. 

6. If p = −2, q = 1 and r = 3 , find the value of 3p²q²r .

p = –2, q = l, r = 3

3p²q²r = 3(–2)² (1)² × 3

= 3 × 4 × 1 × 3 = 36

Challenge Problems

7. LEADERS is a WhatsApp group with 256 members. Every one of its member is an admin for their own WhatsApp group with 256 distinct members. When a message is posted in LEADERS and everybody forwards the same to their own group, then how many members in total will receive that message?

Number of WhatsApp group members = 256

Number of members in each group = 256

Number of members in total will receive that message = 256 × 256

Number of members in total will receive that message = 65536 

8. Find x such that 3^{x +2} = 3^x + 216 .

3^x + 3² –3x = 216

3^x + 9 –3x = 216

3^x (9–1) = 216

3^x  × 8 = 216

3^x = 216 / 8 = 27 = 3³

3^x = 3³

Bases are equal.

So, the powers also equal.

 x = 3.

9. If X = 5x ² + 7x + 8 and Y = 4x ² − 7x + 3 , then find the degree of X+Y.

X = 5x² + 7x + 8

Y = 4x² – 7x + 3

X + Y = 9 x² +11

The degree of X+Y is 2.

10. Find the degree of ( 2a ² + 3ab − b² )− ( 3a ² − ab − 3b² )

2a² + 3ab –b² – 3a² + ab + 3b²

2a² – 3a² + 3ab + ab – b² + 3b²

–a² + 4ab + 2b²

The degree of the expression is 2.

11. Find the value of w, given that x = 3 , y = 4 , z = −2 and w = x² − y ² + z² − xyz .

w = x² –y² + z² –xyz

w = (3)² – (4)² + (–2⁾² – 3 × 4 × –2

 = 9 – 16 + 4 + 24

 = 9 + 4 + 24 – 16

 = 37 – 16 = 21 

12. Simplify and find the degree of 6x ² + 1 – [ 8x – {3x² − 7 − ( 4x² − 2x + 5x + 9)}]

6x² + 1 – [8x– {3x² –7 – (4x² – 2x + 5x + 9)}]

6x² + 1 – [8x –3x² + 7 + (4x² –2x + 5x + 9)]

6x² + 1 – 8x + 3x² –7 – (4x² + 2x –5x –9)

6x² + 3x² – 4x² –8x – 5x + 2x+ 1–7–9

5x² – 13x + 2x + 1 –16

5x² –11x –15

The degree of the expression is 2.

13. The two adjacent sides of a rectangle are 2x² − 5xy + 3z² and 4xy − x ² − z² . Find the perimeter and the degree of the expression.

The two adjacent sides,

Length l = 2x² –5xy + 3z²

Breadth b = 4xy –x² –z²

Perimeter = 2(l + b)

= 2(2x² – 5xy + 3z² + 4xy – x² – z²)

= 2(x² – xy + 2z²)

Perimeter of the rectangle = 2x² – 2xy + 4z²

The degree of the Perimeter is 2. 

ANSWERS:

Exercise 3.4

1. m = 3

2. 6

3. 6

4. −1

5. 6

6. 36

Challenge problems

7. 65536

8. x = 3

9. 2

10. 2

11. 21

12. 5 x² − 11x − 5 ; 2

13. 2x² − 2xy + 4z² ; 2