Summary

DO YOU KNOW

Srinivasa Ramanujan, the great Indian mathematician created so many beautiful equations in his childhood using exponents. Here is an interesting exponential equation from his most popular “Notebooks”.

2² ×6⁶ ×1¹×1¹ =3³ ×3³ ×4⁴

The base and power are equal in each factor.. Moreover the sum of base (or power) in both the sides are also equal. (that is, 2 + 6 + 1 + 1 = 3 + 3 + 4 = 10) . It can be easily proved with the help of laws of exponents.

LHS =2² ×6⁶ ×1¹×1¹ =2² ×6⁶ ×1=2² ×(2×3)⁶

= 2²× 2⁶× 3⁶                  [since, (a × b)^m = a ^m × b^m ]

= 2²⁺⁶ × 3³ + 3³                   [since, a ^m × aⁿ = a^{m +n} ]

= 2⁸ ×3³ ×3³

= 2^2×4 × 3³ × 3³

= ( 2² )⁴ × 3³ × 3³ [since, a ^{m ×n} = ( a^m)ⁿ ]

= 4⁴ ×3³ ×3³ =3³ ×3³ ×4⁴

= RHS.

Try to prove some of his other equations given below:

8⁸ × 9⁹ × 1¹ = 3³ × 3³ × 12¹² (Base total is 18)

4⁴ × 20²⁰ × 30³⁰ × 1¹ = 6⁶ × 24²⁴ × 25²⁵ (Base total is 55)

Summary

● If ‘a’ is any integer, then a × a × a × … × a (n times) = aⁿ . Here ‘a’ is the base and n is the exponent or power or index.

● 

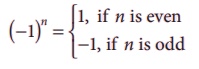
● When a number ‘a’ is multiplied by itself, the product is called the square of that number and denoted by a² . Similarly, the square of a number (a²) is multiplied by ‘a’, then the product is called the cube of that number and is denoted by a³.

● If ‘a’ and ‘b’ are any non-zero numbers and ‘m’ and ‘n’ are natural numbers, then

(i) a^m × aⁿ = a^{m +n} (Product rule)

(ii) a^m ÷ aⁿ = a^{m −n} , m>n (Quotient rule)

(iii) ( a^m )ⁿ = a^{m ×n} (Power rule)

(iv) ( a × b)^m = a ^m × b^m

(v) (a/b) ^m = a^m /b^m

 ● For the base number whose unit digits are 0,1,5 and 6, the unit digit of a number corresponding to any positive exponent remains unchanged.

● For base ending with 4, the unit digit is 4 for odd power and is 6 for even power. Similarly, for base ending with 9, the unit digit is 9 for odd power and is 1 for even power.

● The largest power of a variable in an expression is called its degree. If it has more than one variable, then one has to take the sum of the powers of variables in each term and take the maximum of all these sums.

ICT Corner

Expected outcome

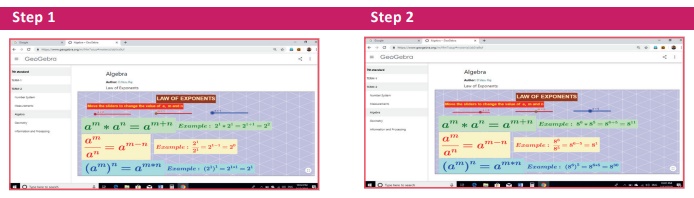
Step-1 : Open the Browser type the URL Link given below (or) Scan the QR Code. GeoGebra work sheet named “Algebra” will open. There is a work sheet named “Law of Exponents”

Step-2 : Move the sliders a, m and n, observe the results and practice the laws.

Browse in the link

Algebra: https://www.geogebra.org/m/f4w7csup#material/ab5ra9uf

or Scan the QR Code.