Laws of Exponents

Laws of Exponents

Let us learn some rules to multiply and divide exponential numbers with the same base.

1. Multiplication of Numbers in Exponential form

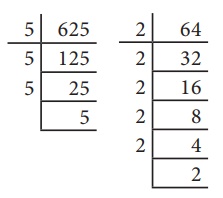
Let us calculate the value of 2³ × 2²

2³ ×2² =(2×2×2)×(2×2)

=2×2×2×2×2

= 2⁵

= 2³⁺²

We observe that the base of 2³ and 2² is the same 2 and the sum of the powers is 5. Now, let us consider negative integers as the base.

(−3)³ × (−3)² = [(−3) × (−3) × (−3)] × [(−3) × (−3)]

                     =(−3) × (−3) × (−3) × (−3) × (−3)

                     =(−3)⁵

                     =(−3)³⁺²

We observe that the base of (−3)³ and (−3)² is the same as (−3) and the sum of the power is 5. Similarly, p ⁴ × p² = ( p × p × p × p) × ( p × p) = p⁶ = p^{4 +2}

Now, for any non-zero integer ‘a’ and whole number ‘m’ and ‘n’, consider a^m and aⁿ . That is, a^m = a × a × a × ... × a (m times) and aⁿ = a × a × a × ... × a (n times)

So, a ^m × aⁿ = a × a × a × ... × a (m times) × a × a × a × ... × a (n times)

                     =a × a × a × ... × a (m+n times) =a^{m +n}

Therefore, a ^m × aⁿ = a^{m +n}

This is called Product Rule of exponents.

Try these

Simplify and write the following in exponential form.

1. 2³ ×2⁵ = 2⁸

2. p ² × p⁴ = p⁶

3. x ⁶ × x⁴ = x¹⁰

4. 3¹×3⁵ ×3⁴ = 3¹⁰

5. (−1)² × (−1)³ × (−1)⁵ = (–1)¹⁰

Example 3.7

Simplify using Product Rule of exponents.

(i) 5⁷ × 5³

(ii) 3³ × 3² × 3⁴

(iii) 25 × 32 × 625 × 64

Solution

(i) 5⁷ × 5³ = 5⁷⁺³

[since, a ^m × aⁿ = a^{m +n} ]

= 5¹⁰

(ii) 3³ ×3² ×3⁴ =3³⁺² ×3⁴ =3⁵ × 3⁴

= 3⁵⁺⁴ = 3⁹

iii) 25×32×625×64 =(5×5)×(2×2×2×2×2) × (5×5×5×5)×(2×2×2×2×2×2)

                              =5² ×2⁵ ×5⁴ ×2⁶

                              = (5² × 5⁴) × (2⁵ × 2⁶) [grouping exponential numbers with the same base]

                              = 5²⁺⁴ × 2⁵⁺⁶ = 5⁶ × 2¹¹

2. Division of Numbers in Exponential form

Let us calculate the value of 2⁵ ÷ 2²

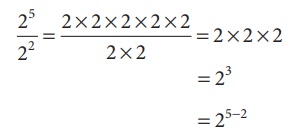
Note

Can you find the value of a ² × a⁰ ?

By Product Rule,

a ² × a⁰ = a^{2 +0}

a ² × a⁰ = a²

a⁰ = a² / a² = 1

[dividing by a² on both sides]

Therefore, a⁰ = 1 , a ≠ 0 .

We observe that the base of 2⁵ and 2² is the same ‘2’ and the difference of powers is 3. Now, let us consider negative integers as the base.

Consider (−5)³ ÷ (−5)²

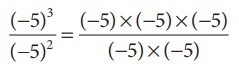
(−5)³ / (−5)² = [(−5) × (−5) × (−5)] / [(−5) × (−5)]

= (−5)¹ = (−5)³⁻²

We observe that the base of (–5)³ and (–5)² is the same as (–5) and the difference of the power is 1.

Thus, we can observe that for any non-zero integer ‘a’ and for whole numbers ‘m’ and ‘n’, consider a^m and aⁿ , m > n .

That is,    a^m = a × a × a × ... × a (m times); aⁿ = a × a × a × ... × a (n times)

a^m / aⁿ  = [ a × a × a... × a (m times) ] / [ a × a × a... × a (n times) ] = a × a × a... × a (m − n times ) = a^{m −n}

Therefore,  a^m / aⁿ  = a^{m −n}

This is called Quotient Rule of exponents.

Example 3.8

Simplify using quotient rule of exponents.

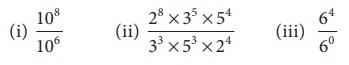
Solution

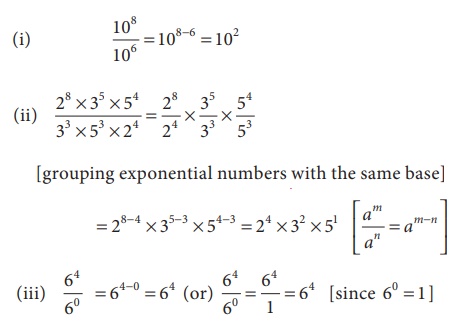
Think

What is Half of 2¹⁰ ? Ragu claims the answer is 2⁵ . Is he correct ? Discuss.

Try these

Simply the following.

1. 23⁵ ÷ 23² = 23³

2. 11⁶ ÷ 11³ = 11³

3. (−5)³ ÷ (−5)² = (–5)

4. 7³ ÷7³ = 1

5. 15⁴ ÷ 15 = 15³

3. Power of Exponential form

Let us find the value of (2²)⁵

( 2²)⁵ = 2² × 2² × 2² × 2² × 2² = 2^{2 + 2 + 2 + 2 +2} (By Product rule)

2¹⁰ = 2^2×5

Similarly, (3³)⁴ =3³ ×3³ ×3³ ×3³

= 3^3+3+3+3 = 3¹² = 3^3×4

(5⁶ )² = 5⁶ × 5⁶ = 5⁶⁺⁶ = 5¹² = 5^6×2

In general, for any non-zero integer ‘a’ and whole number ‘m’ and ‘n’,

( a^m )ⁿ = (a ^m × a ^m × a^m ... × a^m ) (n times)

= a^{m + m +m...+m (n times)}

= a^{m ×n}

Hence, ( a ^m )ⁿ = a^{m ×n}

This is called Power Rule of exponents.

Try these

Simplify and write the following in exponent form.

1. (3²)³ = 3⁶

2. [(−5)³]² = (–5)⁶

3. (20⁶)² = (20)¹²

4. (10³)⁵ =(10)¹⁵

Example 3.9

Simplify using power rule of exponents.

(i) ( 8³ )⁴

(ii) (11⁵ )²

(iii) ( 2⁶ )² × ( 2⁴ )⁷

Solution

(i)  (8³)⁴ = 8^3×4 = 8¹²  [since ( a ^m )ⁿ = a^m×n ]

(ii) (11⁵ )² = 11^5×2 = 11¹⁰ [since ( a ^m )ⁿ = a^{m ×n} ]

(iii) (2⁶ )² × (2⁴)⁷ = 2^6×2 × 2^4×7 [since ( a ^m )ⁿ = a^{m ×n} ]

= 2¹² × 2²⁸

= 2¹² +2²⁸ = 2⁴⁰

[since (a^m × aⁿ = a^m+n ]

Think

We learnt that 2² = 2 × 2 .

What is the value of 2²² ? Discuss.

4. Exponent Numbers with Different Base and Same Power

1. To understand the multiplication of exponent numbers with different base and same powers, let us consider the following example,

10⁵ = 10 ×10 ×10 ×10 ×10

= (2×5)×(2×5)×(2×5)×(2×5)×(2×5)

= (2×2×2×2×2)×(5×5×5×5×5)

10⁵ =2⁵ ×5⁵

But we know that, 10 = 2 × 5. Hence 10⁵ = (2 × 5)⁵ = 2⁵ × 5⁵ .

In general, for any non-zero integers ‘a’ and ‘b’ and for whole number ‘m’ ( m > 0),

a ^m × b^m = a × a × a × ... × a (m times) × b × b × b × ... × b (m times)

= (a × b) × (a × b) × (a × b) × ... × (a × b) (m times) = (a × b)^m

Therefore, a ^m × b^m = (a × b)^m .

2. To understand the division of exponent numbers with different base and same powers, let us consider the follwing example,

10⁵ = 10 ×10 ×10 ×10 × 10

= (20/2) × (20/2) ×(20/2) ×(20/2) ×(20/2)

= [20×20×20×20×20] / [2×2×2×2×2]

Therefore, 10⁵ = 20⁵ / 2⁵ . But we know that, 10 = (20/2).

 Hence, 10⁵ = (20/2)⁵ = 20⁵ / 2⁵.

Hence, for any two non-zero integers ‘a’ and ‘b’ and a whole number ‘m’ ( m > 0),

(a/b)^m = (a/b) × (a/b) × (a/b) × . . . (a/b) (m times)

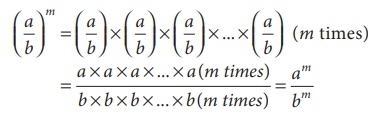
= [ a × a × a × ... × a (m times)] / [ b × b × b × ... × b (m times) ] = a^m / b^m

Therefore, .

(a/b)^m = a^m / b^m

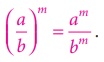
Try these

1. Express the following exponent numbers using a^m × b^m = (a × b)^m .

(i) 5² ×3² = (5 × 3)² = 15²

(ii) x ³ × y³ = (xy)³

(iii) 7⁴ ×8⁴ = (7 × 8)⁴ = 56⁴

2. Simplify the following exponent numbers by using (a/b)^m = a^m / b^m

(i) 5³ ÷2³ = 5³ / 2³ = (5 / 2)³

(ii) (−2)⁴ ÷ 3⁴ = ( –2)⁴ / 3⁴ = (– 2 / 3)⁴

(iii) 8⁶ ÷5⁶ = 8⁶ / 5⁶ = (8 / 5)⁶

(iv) 6³ ÷ (−7)³ = 6³ /(–7)³ = (6 / –7)³

Example 3.10

Simplify by using the law of exponents.

(i) 7⁶ × 3⁶

(ii) 4³ × 2³ × 5³

(iii) 72⁵ ÷ 9⁵

(iv) 6¹³ × 48¹³ ÷ 12¹³

Solution

(i) 7⁶ ×3⁶ = (7×3)⁶ =21⁶        [Since, a^m × b^m = (a × b)^m ]

(ii) 4³ ×2³ ×5³ =(4×2×5)³ = 40³  [Rule extended for 3 numbers]

(iii) 72⁵ ÷ 9⁵ = (72÷9)⁵ = 8⁵ [Since, a^m / b^m = (a / b)^m ]

(iv) 6¹³ × 48¹³ ÷ 12¹³ = 6¹³ × (48¹³ ÷ 12¹³ ) [BIDMAS]

= 6¹³ × (48/12)¹³  [Since, a ^m / b^m = (a / b)^m ]

= 6¹³ × 4¹³

= (6 × 4)¹³           [Since, a ^m × b^m = (a × b)^m ]

= (24)¹³

1. All the 10 digits appear once in the expansion of 32043². That is, the value of 32043² = 1026753849 .

2. There are beautiful equations with same exponent consecutive natural numbers as the base.

3²+4² =5²

10² + 11² + 12² = 13² + 14²

Activity

Finding the pair

Divide the classroom into two groups. Each group will have a set of cards. Each member of Group 1 has to pair with one suitable member of Group 2 by stating the reason.

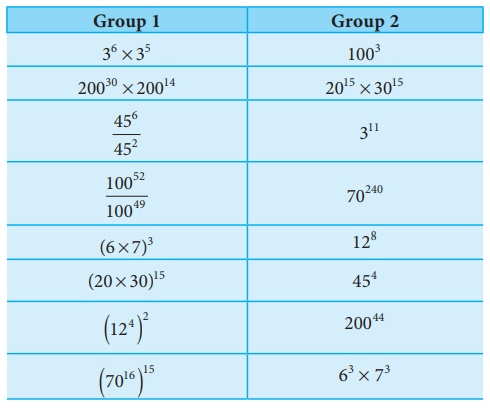
This activity can be extended till all the children in the class are familiarise with the laws of exponents.