Types of Moduli of Elasticity

TYPES OF MODULI OF ELASTICITY

      Depending upon the three of strain, there are three types of elastic moduli, viz.

a)                    Young’s Modulus(Y) or modulus corresponding to longitudinal strain

b)                   Bulk modulus(K) or modulus corresponding to the volume strain

c)                    Rigidity modulus(N) or modulus corresponding to the shearing strain.

1 YOUNGS MODULUS(Y)

DEFINITION: it is defined as the ratio between the longitudinal stress to longitudinal strain, within the elastic limits,

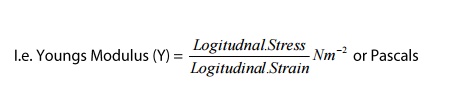
i.e youngs Modulus(Y)= Logitudnal Stress\ Logitudinal Strain Nm^-2 or pascals

Explanation: Let us consider a wire of length ‘L’ with an area of cross section ‘A’. Let one end of the wire is fixed and the other end is loaded or stretched as shown in the figure.

Let ‘I’ be the change in length due to the action of the force, then

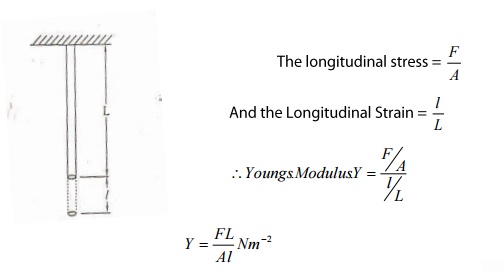
2 BULK MODULUS

DEFINITION: it is defined as the ration between the volume stress or bulk strain with in the elastic limits

Bulk Modulus (K) =Bulk Stress\Bulk Strain Nm^-2

Explanation: Let us consider a body of volume ‘V’ with an area of cross section ‘A’. Let three equal forces act on the body in mutually perpendicular directions as shown in the figure. Let ‘V’ be the change in volume, due to the action of forces, then

The volume stress or bulk stress=F\A

The volume strain or bulk strain=v\V

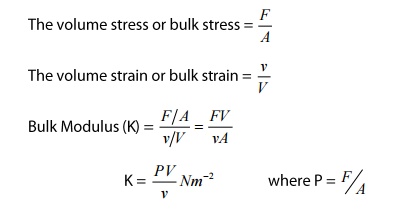
Bulk Modulus (K) = (F\A)\(v\V)=FV\vA

K=PV\v Nm^-2

Where,

P=F\A

3 RIGIDITY MODULUS

Definition: it is defined as the ratio between the tangential stress to the shearing strain within the elastic limit.

Rigidity Modulus (n)=Tangential Stress\Tangential Strain Nm^-2

Explanation: Let us consider a solid cube ABCDEFGH wherein lower CDHG is fixed as applied over the figure. A tangential force ‘F’ is applied over the upper face ABEF. The result is that the cube gets deformed into rhombus shape A’B’CDE’F’GH i.e the lines joining the two faces are shifted to an angle ø. If ‘L’ is the original ‘l’ is the relative displacement of the upper face of the cube with respect to the lower fixed face, then

We can write the tangential stress=F\A

The shearing stress ø cam be defined as the ration of the relative displacement between the two layers in the direction of the stress, to the distance measured perpendicular to the layer.

Rigidity Modulus (n)=tangential stress\Shearing strain=F\AøNm^-2

4 POISSONS RARIO

DEFINITION: It is defined as the ratio between the lateral strain per unit stress (β) to the longitudinal strain per unit stress (α), within the elastic limits.

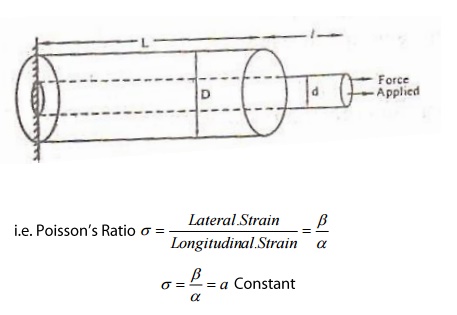
Explanation: Let us consider a wire, fixed at one end and is stretched alomg the other end as shown in the figure.

Due to force applied the wire becomes longer but it also becomes thinner i.e although there is an increase in its length, there is a decrease in its diameter as shown in the figure. Therefore the wire elongates freely in the direction of tensile force and contracts laterally in the direction perpendicular to the force. Let ‘L’ be the original length and ‘D’ be the original diameter of the wire after the application of force, let the length increase from L to L+l and the diameter decrease from D and d, then

Longitudinal Strain=l\L

And Lateral Strain=(D-d)\D

The negative sign indicates that longitudinal strain and lateral strain are opposite to each other.