Modes of Heat Transer

MODES OF HEAT TRANSFER

Heat is one of the forms of energy. It is transmitted from one place to another by three different ways.

They are

Conduction

Convection

Radiation

1 Thermal conduction

It is well known fact that is conducted through the material of the body. In conduction, heat transfer takes place from one point to another through a material medium without the actual movement of the particles in that medium.

The heat is transmitted from a body of higher temperature to that o lower temperature.

As an example, when a metal rod is heated at one end, the heat gradually lows along the length o the rod and the other end o the rod also becomes hot after some time. This shows that heat has travelled through the molecules of the rod from one end to other. The molecules in the rod remain fixed in their mean positions.

On heating the energy molecules increases and they start vibrating about their mean positions. They collide with the neighbouring molecules. Because of this collision, the neighbouring molecules are set into vibration.

Each molecule thus transfers some of the heat it receives from its predecessor to its successor. Thus the transmission of heat takes place by molecular vibration in case of conduction.

DEFINITION

It is the process of transmission of heat from one point to another through substance (or some medium) without the actual motion o the particles.

Conduction always requires some material medium. The material medium must be solid. As it requires medium, the conduction process takes place over vacuum. In fluids (liquid and gas), heat transmission is through the process of convection.

2 Thermal Conductivity

The ability of a substance to conduct heat energy is measured by thermal conductivity

EXPRESSION OR THERMAL CONDUCTIVITY

Consider a slab of material of length x meter and area of cross section A as shown in the figure.

One end of the slab is maintained at a higher temperature θ₁ and the other end at a lower temperature is θ_1. Heat flows from the hot end to the cold end. It is found that the amount of heat(Q) conducted from one end to another end is

Directly proportional to the area of cross-section(A)

Directly proportional to the temperature dierence between the end θ₁- θ₂

 Directly proportional to the time of conduction(t)

Directly proportional to the length of (x).

Where K is the proportionality constant. It is known as coefficient of thermal conductivity or simple or thermal conductivity. Its value depends upon the natue of the material.

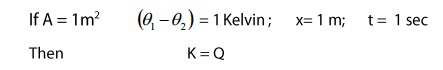
The condition define the coefficient of Thermal conductivity

Definition:

It is defined as the amount of heat conducted per second normally across unit area of cross-section of the material per unit temperature difference per uint length.

The quantity (θ₁- θ₂) / x denote the rate of fall of temperature with respect to distance. It is know as temperature gradient.

The negative sign indicates the fall of temperature with distance.

Unit:

 3 Newton's Law of Cooling

Statement:

It state that the rate at which a body loses heat is directly proportional to the temperature difference between the body and that of the surrounding.

The amount of heat radiated depends upon the area and nature of the radiating surface.

If ‘θ’ is the temperature of the body at any instant and ‘θo’ the temperature of the surroundings, then according to Newton’s law of cooling, heat lost is proportional to the difference of temperature between the body and surroundings i.e.( θ₁- θ_o)

If dQ is the quantity of heat lost in a small time dt, then

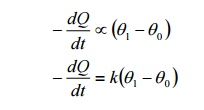
Where k is the constant depending upon the area and the nature o the radiating surface. The negative sign indicates that there is decrease of heat with time.

Expression when a heat body cools from θ₁^oC to θ₂^oC in time t

Consider a body of mass m, specific heat capacity S and at temperature θ. Suppose the temperature falls by a small amount dθ in time dt.

Thus, the amount of heat lost

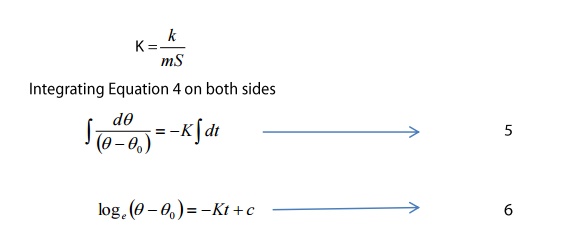
 Where c is the constant of integration this equation is of the form

y=mx+c and it represents a Straight line.

If the cooling takes place rom θ₁^o C to θ₂^oC in time t then taking the limits, we have

4. VERIICTION O NEWTON’S LAW O COOLING

The given empty spherical calorimeter is filled with boiling water and a thermometer is kept in the orifice as shown in the figure. When the temperature reaches 800C, a stop clock is started. The time taken for every 2^oC fall in temperature is noted, till the temperature reaches 60 ^oC.

The rate of cooling at various temperature is determined. A graph is drawn with rate of cooling along y-axis and the excess of temperature of the calorimeter over the surrounding along the x-axis.

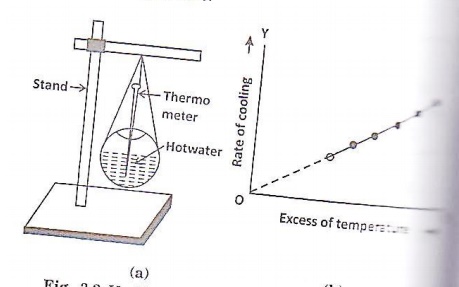
The graph is found to be a straight line, thereby, showing that the rate of cooling is proportional to the excess of temperature.

Limitations

The temperature difference between the hot body and surrounding should be low.

The heat loss is only by radiation and convection.

The temperature of hot body should be Uniform throughout.

Applications

The specific heat capacity of the liquid is determined by using this law.

5 RECTILINEAR FLOW OF HEAT THROUGH A ROD

Consider a long rod AB of Uniform cross section heated at one end A as shown in the figure. Then there is low of heat along the length o the bar and heat is also radiated from its surface. B is the cold end.

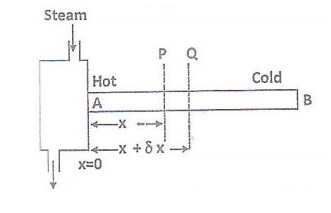
Consider the low of heat between the section P and Q at distance x and x+δx rom the hot end. Excss temperature at Section P above the surroundings=θ

6 BEORE THE STEADY STATE REACHED

Before the steady state is reached, the amount of heat Q is used in two ways. A part of the heat is used in raising the temperature of the rod and the remaining heat is lost by radiation from the surface o the element.

Heat absorbed per second to raise the temperature of the rod

The equation 8 is the standard differential equation for the flow of heat through the rod.

SPECIAL CASE

The thermal conductivity of any material is determined using equation 8 by considering the actual condition of the material.

Case 1: When heat is lost by radiation is negligible

If the rod is completely covered by some insulating materials, then there is no loss of heat due to radiation. Hence, the heat lost by radiation Epδxθ is zero.

In that case, the total heat gained by the rod is completely used to raise the temperature of the rod.

From equation 8

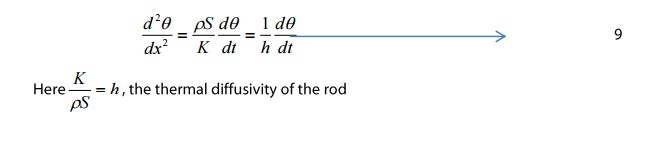
Case 2: After the steady state is reached

After the steady state is reached, there is no raise of temperature.

Here A and B are two unknown constants which can be determined from the boundary conditions of the problem.

Suppose the bar is of infinite length

Excess o temperature above the surroundings of the hot end = θ_o

Temperature of the other end (cold end) = 0

This equation 12 represents the excess of temperature of a point at distance x from the hot end after the steady state is reached and it represents an exponential curve.

The temperature falls exponentially from the hot end as shown in the figure.

7 HEAT CONDUCTION THROUGH A COMPOUND MEDIA OF TWO LAYERS BODIES IN SERIES

Let us consider a composite slab (or compound wall) of two different materials A and B with thermal conductivities K₁ and K₂ and of thickness x₁ and x₂.

The temperature of the outer aces of A and B are θ₁ and θ₂.

The temperature of the surface in contact is θ. When the steady state is reached, the amount of heat flowing per second(Q) through every is same.

Amount of heat flowing through the material(A) per second

‘Q’ is the value o heat lowing through the compound wall of the two materials

The method can be extended to composite slab with more than two slabs.

In general for any number of walls or slabs, the amount of heat conducted is

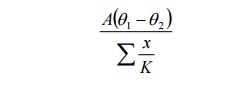
Bodies in Parallel

Let us consider a composite slab (or Compound wall) of two dierent materials A and B with thermal conductivities K₁ and K₂ and o thickness x₁ and x₂. They are arranged in parallel as shown in the figure.

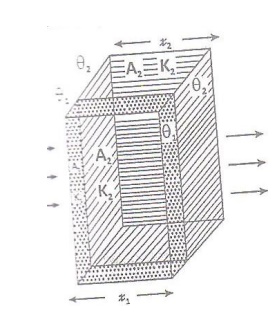
Let the faces of the material be at temperature θ₁ and the respective other end aces be at θ₂ temperature.

A1 and A2 be the ares o cross section of the materials

Amount of heat flowing through the irst material (A) in one second

8 Methods to determine Thermal conductivity

The thermal conductivity of a material is determined by different methods.

1.     Searle’s Method – or good conductor like Metallic rod

2.     Forbe’s Method – for determining the absolute conductivity of metal

3.     Lee’s Disc method – for bad conductors

4.     Radial Flow method – or Bad conductors.