Radial flow of heat

Radial low of heat

In this method, heat flows from the inner side towards the other side along the radius of the cylindrical shell.

This method is interesting because there is no loss of heat as in the other methods.

Cylindrical Shell method

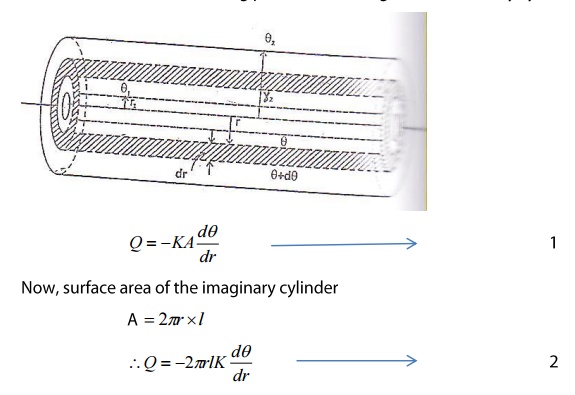
Consider a cylindrical tube of length l, inner radius r1 and outer radius r2 as shown in the figure. The tube carries steam or some hot liquid.

Heat is conducted radially across the wall of the tube. After the steady state is reached, the temperature of the inner surface θ₁ and on the outer surface θ_2. This thick pipe is imagined to consist of a large number of thin coaxial cylinders of increasing radius. Any such thin imaginary cylinder of the material of thickness ‘dr’ at a distance r from the axis of the pipe is taken.

Amount of heat flowing  per second through this elementary cylinder

After steady state is reached, the amount of heat lowing(Q) through all imaginary cylinders is same.

Rearranging, the equation 2, we get

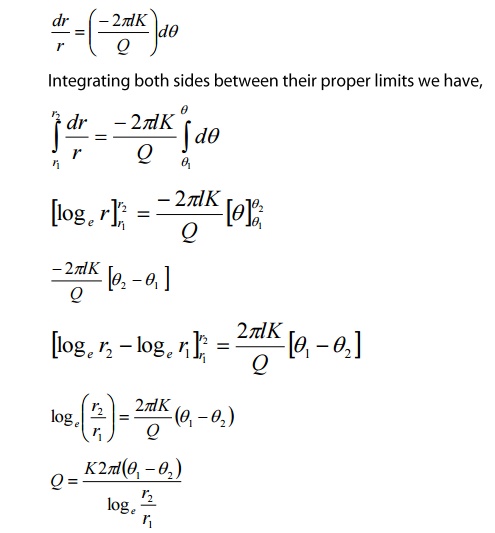
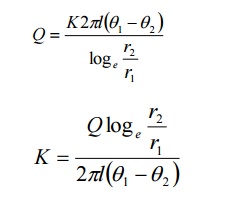
THERMAL CONDUCTIVITY OF RUBBER

Principle:

It is based on the principle of radial low of heat through a cylindrical shell.

Procedure:

A big empty calorimeter with stirrer is weighted (W1). It is then illed with two thirds of water and again weighted(W2). A known length(l) of a rubber tube is immersed in water in the calorimeter as shown in the figure.

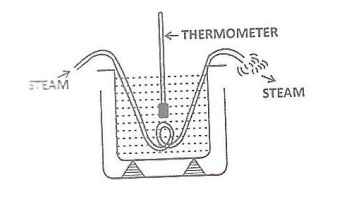
The calorimeter is stirred dwell and the initial temperature θ₁^oC is noted. Now one end of the rubber tube is connected to a steam generator and steam is passed through it. The steam is passed continuously till there is rise of 10 ^oC in temperature. The time taken (t second) or this rise in temperature is noted. The inal temperature of the water θ₂ ^oC in the calorimeter is also noted .

Observation

Mass of the empty calorimeter with stirrer = W₁ kg

Mass of the calorimeter with water = w₂ kg

Mass of the water = (W₂-W₁) kg

Initial temperature of the water = θ₁ ^oC

Final temperature of the water = θ₂ ^oC

Rise in temperature of the water = (θ₁ -θ₂)

Time for which steam is passed = t seconds

Length o the rubber tube immersed in water = l

Inner radius of the rubber tube = r₁

Outer radius of the rubber tube = r₂

Specific heat capacity of  Calorimeter = S₁

Specific heat capacity of  Water = S₂

Heat gained by the calorimeter = Mass x Specific heat capacity x change in temperature

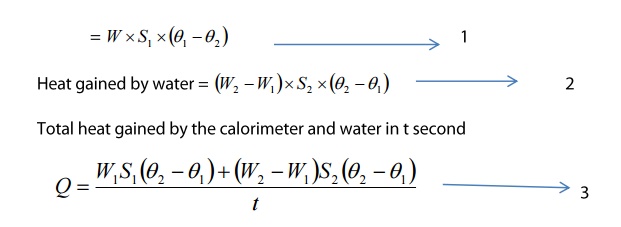
The expression for the thermal conductivity (K) in the case o cylindrical shell method is given by