Two Dimensional Clipping and Viewing

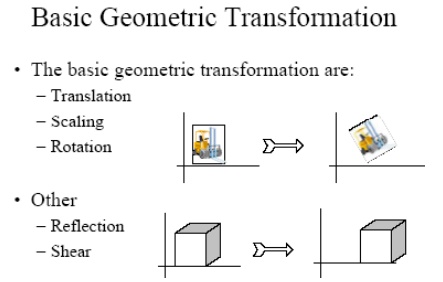
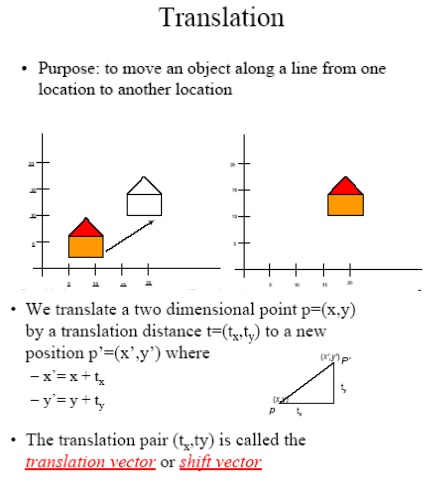
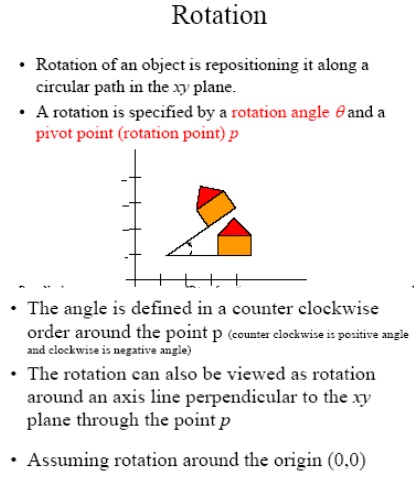
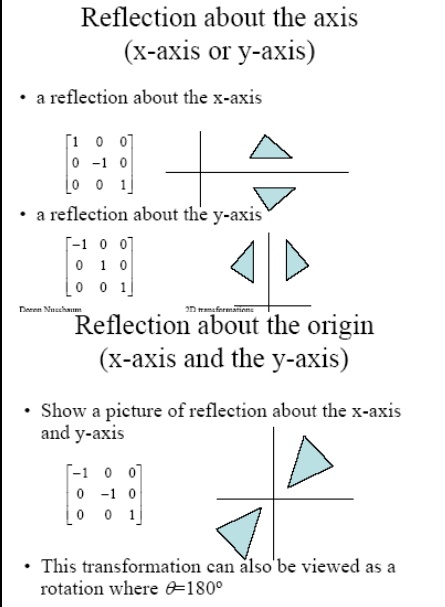
TWO DIMENSIONAL GEOMETRIC TRANSFORMATIONS

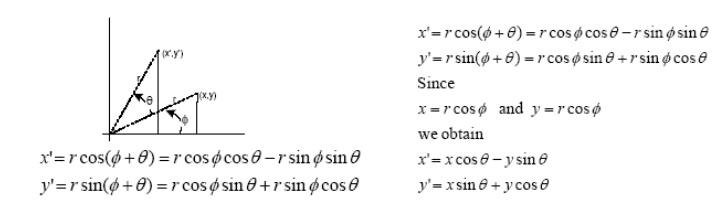
TWO DIMENSIONAL CLIPPING AND VIEWING

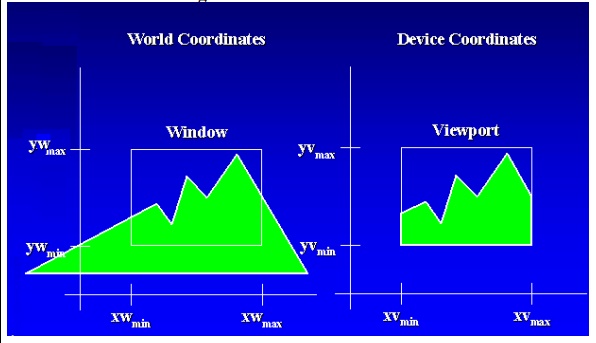
The Viewing Pipeline

•Window

•A world-coordinate area selected for display. defines what is to be viewed

•Viewport

•An area on a display device to which a window is mapped. defines where it is to be displayed

•Viewing transformation

•The mapping of a part of a world-coordinate scene to device coordinates.

•A window could be a rectangle to have any orientation.

Two-Dimensional Viewing

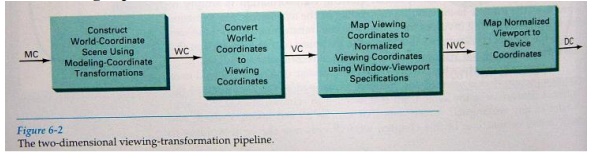
The Viewing Pipeline

Viewing Effects

•Zooming effects

Successively mapping different-sized windows on a fixed-sized viewports.

•Panning effects

Moving a fixed-sized window across the various objects in a scene.

•Device independent

Viewports are typically defined within the unit square (normalized coordinates)

Viewing Coordinate Reference FrameThe reference frame for specifying the world-coordinate window.

•Viewing-coordinate origin: P0 = (x0, y0)

•View up vector V: Define the viewing yv direction

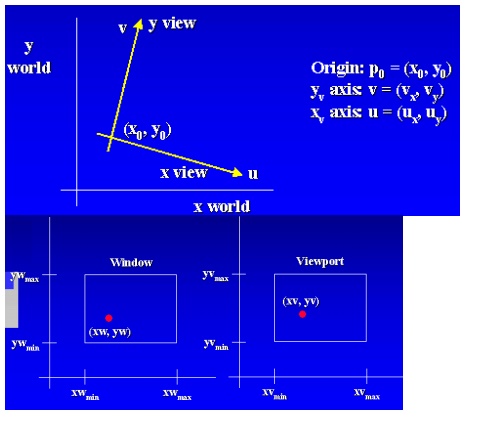
Window-to-Viewport Coordinate Transformation

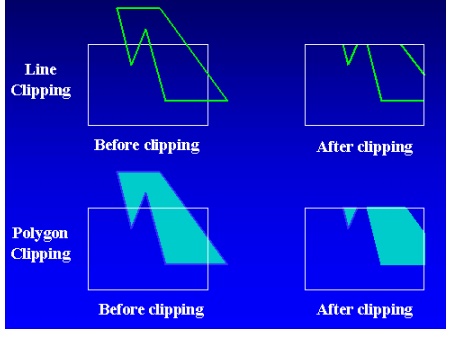
Clipping Operations

•         Clipping

•        Identify those portions of a picture that are either inside or outside of a specified region of space.

•         Clip window

•        The region against which an object is to be clipped.

•        The shape of clip window

•         Applications of clipping

•         World-coordinate clipping

Clipping Operations

•         Viewport clipping

•        It can reduce calculations by allowing concatenation of viewing and geometric transformation matrices.

•         Types of clipping

•        Point clipping

•        Line clipping

•        Area (Polygon) clipping

•        Curve clipping

•        Text clipping

•         Point clipping (Rectangular clip window)

Line Clipping

Possible relationships between line positions and a standard rectangular clipping region

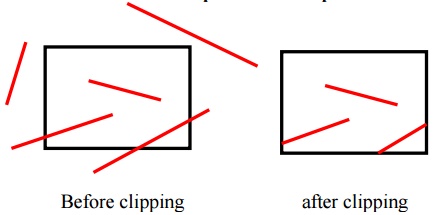
•         Possible relationships

–   Completely inside the clipping window

–   Completely outside the window

–   Partially inside the window

•         Parametric representation of a line

x = x1 + u(x2 - x1) y = y1 + u(y2 - y1)

•         The value of u for an intersection with a rectangle boundary edge

–   Outside the range 0 to 1

–   Within the range from 0 to 1

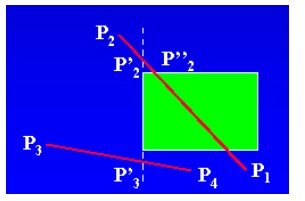
Cohen-Sutherland Line Clipping

•         Region code

–   A four-digit binary code assigned to every line endpoint in a picture.

–   Numbering the bit positions in the region code as 1 through 4 from right to left.

•         Bit values in the region code

•        Determined by comparing endpoint coordinates to the clip boundaries

•        A value of 1 in any bit position: The point is in that relative position.

•         Determined by the following steps:

•        Calculate differences between endpoint coordinates and clipping boundaries.

•         Use the resultant sign bit of each difference calculation to set the corresponding bit value.

•         The possible relationships:

•        Completely contained within the window

•        0000 for both endpoints.

•        Completely outside the window

•        Logical and the region codes of both endpoints, its result is not 0000.

•        Partially

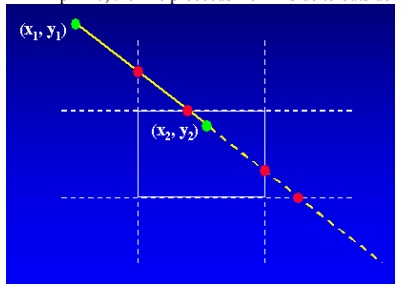
Liang-Barsky Line Clipping

Rewrite the line parametric equation as follows:

•         pk = 0, parallel to one of the clipping boundary

•        qk < 0, outside the boundary

•        qk >= 0, inside the parallel clipping boundary

•         pk < 0, the line proceeds from outside to the inside

•         pk > 0, the line proceeds from inside to outside

Nicholl-Lee-Nicholl Line Clipping

•         Compared to C-S and L-B algorithms

•        NLN algorithm performs fewer comparisons and divisions.

•        NLN can only be applied to 2D clipping.

•         The NLN algorithm

•        Clip a line with endpoints P1 and P2

•         First determine the position of P1 for the nine possible regions.

•        Only three regions need be considered

•        The other regions using a symmetry transformation

•        Next determine the position of P2 relative to P1.

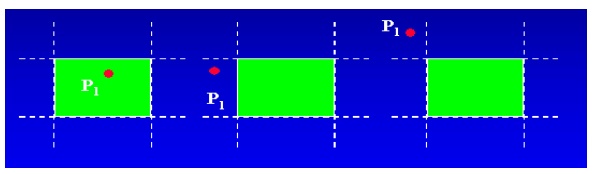
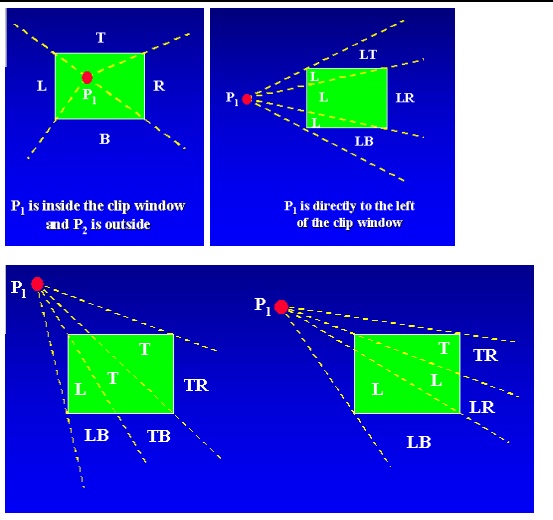
•         To determine the region in which P2 is located

–   Compare the slope of the line to the slopes of the boundaries of the clip region.

–   Example: P1 is left of the clipping rectangle, P2 is in region LT.

Polygon Clipping

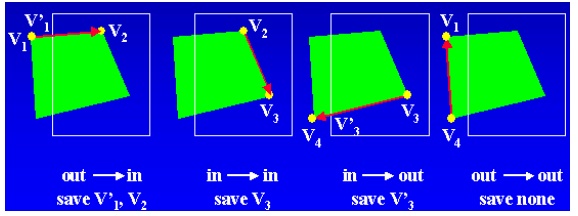
Sutherland-Hodgeman Polygon Clipping

•         Processing the polygon boundary as a whole against each window edge

•         Processing all polygon vertices against each clip rectangle boundary in turn

•         Pass each pair of adjacent polygon vertices to a window boundary clipper

There are four cases:

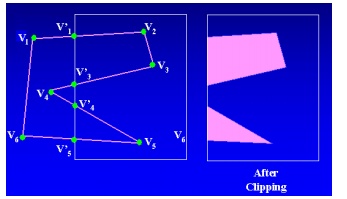
•         Intermediate output vertex list

•        Once all vertices have been processed for one clip window boundary, it is generated.

•        The output list of vertices is clipped against the next window boundary.

•        It can be eliminated by a pipeline of clipping routine.

•         Convex polygons are correctly clipped.

•         If the clipped polygon is concave

•        Split the concave polygon

Weiler-Atherton Polygon Clipping

•           Developed as a method for identifying visible surfaces

•        It can be applied with arbitrary polygon-clipping region.

•        Not always proceeding around polygon edges

•        Sometimes follows the window boundaries

•         For clockwise processing of polygon vertices

•        For an outside-to-inside pair of vertices, follow the polygon boundary.

•        For an inside-to-outside pair of vertices, follow the window boundary in clockwise direction.

•         Curve clipping

•        Use bounding rectangle to test for overlap with a rectangular clip window.

•         Text clipping

•        All-or-none string-clipping

•        All-or-none character-clipping

•        Clip the components of individual characters