Line-Drawing Algorithms

LINE-DRAWING ALGORITHMS

Design of Line and Circle Algorithms

Basic Math Review

3.     Line drawing is accomplished by calculating intermediate positions along the line path between specified end points.

Precise definition of line drawing

4. Given two points P and Q in the plane, both with integer coordinates, determine which pixels on a raster screen should be on in order to make a picture of a unit-width line segment starting from P and ending at Q.

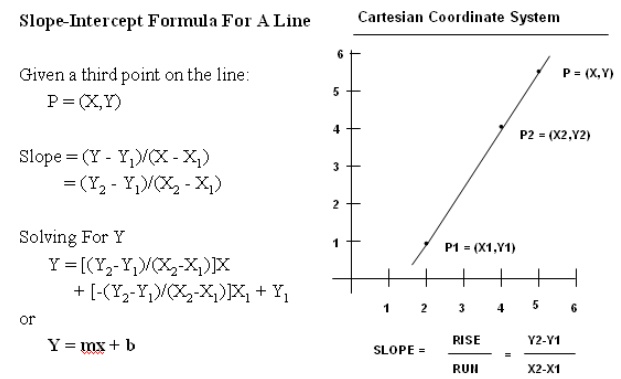
The thinnest line is of one-pixel wide. We will concentrate on drawing a line of 1 pixel resolution. The Cartesian slope-intercept equation for a straight line is

y= m. x + b

m is the slope of the line and b is the y intercept.

Given the endpoints of a line segment. m = y2-y1 / x2-x1

b= y1-m.x1

5. Also for any given interval ∆x along a line, we can compute the corresponding y interval ∆y from ∆y= m. x

6. Similarly we can obtain the x interval ∆x corresponding to a specified ∆y as ∆x= ∆y / m

7.     These equations form the basis for determining deflection voltages in analog devices.

8.     Also , for any given x interval ∆x along a line, we can compute the corresponding y interval ∆y from ∆y= m. ∆ x

9.     These equations form the basis for determining deflection voltages in analog devices.

10.              On Raster systems, lines are plotted with pixels, and step sizes in the horizontal and vertical directions are constrained by pixel separations. Hence we ought to “sample” a line at discrete positions and determine the nearest pixel to the line at each sampled position

DDA ALGORITHM

The digital differential analyzer (DDA) samples the line at unit intervals in one coordinate corresponding integer values nearest the line path of the other coordinate.

The following is thus the basic incremental scan-conversion(DDA) algorithm for line drawing for x from x0 to x1

Compute y=mx+b

Draw_fn(x, round(y))

Major deficiency in the above approach : Uses floats

Has rounding operations

Bresenham’s Line Algorithm

ⁿ  An accurate, efficient raster line drawing algorithm developed by Bresenham, scan converts lines using only incremental integer calculations that can be adapted to display circles and other curves.

ⁿ  Keeping in mind the symmetry property of lines, lets derive a more efficient way of drawing a line.

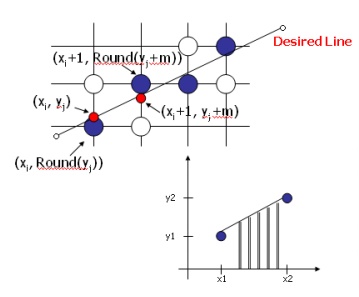
Starting from the left end point (x0,y0) of a given line , we step to each successive column (x position) and plot the pixel whose scan-line y value closest to the line path

Assuming we have determined that the pixel at (xk,yk) is to be displayed, we next need to decide which pixel to plot in column xk+1.

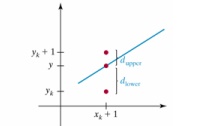
Choices are(xk +1, yk) and (xk+1, yK+1) 

d1 = y – yk = m(xk + 1) + b – yk

d2 = (yk + 1) – y = yk + 1- m(xk + 1) – b

ⁿ   The difference between these 2 separations is d1-d2 = 2m(xk + 1) – 2 yk + 2b – 1

ⁿ   A decision parameter pk for the kth step in the line algorithm can be obtained by rearranging above equation so that it involves only integer calculations

ⁿ  Define  Pk =  x ( d1-d2) = 2  yxk-2      xyk + c

ⁿ   The sign of Pk is the same as the sign of d1-d2, since    x > 0.

Parameter c is a constant and has the value 2 y + x(2b-1) (independent of pixel position)

ⁿ  If pixel at yk is closer to line-path than pixel at yk +1

(i.e, if d1 < d2) then pk is negative. We plot lower pixel in such a case. Otherwise , upper pixel will be plotted.

ⁿ   At step k + 1, the decision parameter can be evaluated as, pk+1 = 2 yxk+1 - 2 xyk+1 + c

ⁿ   Taking the difference of pk+ 1 and pk we get the following.

pk+1 – pk = 2 y(xk+1- xk)-2 x(yk+1 – yk)

ⁿ  But, xk+1 = xk +1, so that

pk+1 = pk + 2  y - 2  x(yk+1 – yk)

ⁿ  Where the term yk+1-yk is either 0 or 1, depending on the sign of parameter pk

ⁿ   The first parameter p0 is directly computed

p0 = 2 yxk - 2  xyk + c = 2              yxk – 2            y +      x (2b-1)

  Since (x0,y0) satisfies the line equation , we also have

     y0 =       y/       x * x0 + b

  Combining the above 2 equations , we will have

     p0 = 2    y –     x

The constants       2  y and 2  y-2  x are calculated once for each   time to be scan converted

  So, the arithmetic involves only integer addition and subtraction of 2 constants

ALGORITHM

Input the two end points and store the left end point in (x0,y0)

Load (x0,y0) into the frame buffer  (plot the first point)

Calculate  the  constants   x,      y,  2        y and  2   y-2      x  and  obtain  the  starting value  for  the  decision

parameter as

p0 = 2      y-        x

At each xk along the line, starting at k=0, perform the following test:

If pk < 0 , the next point is (xk+1, yk) and

pk+1 = pk + 2 y OtherwisePoint to plot is (xk+1, yk+1)

pk+1 = pk + 2 y - 2 x Repeat step 4 (above step) x times