Circle/ Curve -Generating Algorithms

CIRCLE/ CURVE -GENERATING ALGORITHMS

Properties of a circle:

n    A circle is defined as a set of points that are all the given distance (xc,yc). This distance relationship is expressed by the pythagorean theorem in Cartesian coordinates as

(x – xc)2 + (y – yc) 2 = r2

n    We could use this equation to calculate the points on the circle circumference by stepping along x-axis in unit steps from xc-r toxc+r and calculate the corresponding y values at each position as

y = yc +(- ) (r2 – (xc –x )2)1/2

n    This is not the best method:

n   Considerable amount of computation

n   Spacing between plotted pixels is not uniform

Polar co-ordinates for a circle

nWe could use polar coordinates r and θ,

x = xc + r cosθ  y = yc + r sinθ

nA fixed angular step size can be used to plot equally spaced points along the circumference

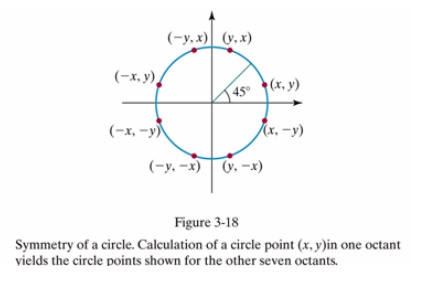
nA step size of 1/r can be used to set pixel positions to approximately 1 unit apart for a continuous boundary nBut, note that circle sections in adjacent octants within one quadrant are symmetric with respect to the 45 deg line dividing the to octants

nThus we can generate all pixel positions around a circle by calculating just the points within the sector from x=0 to x=y

nThis method is still computationally expensive

Midpoint Circle Algorithm

n    We will first calculate pixel positions for a circle centered around the origin (0,0). Then, each calculated position (x,y) is moved to its proper screen position by adding xc to x and yc to y

n    Note that along the circle section from x=0 to x=y in the first octant, the slope of the curve varies from 0 to -1

n    Circle function around the origin is given by

fcircle(x,y) = x2 + y2 – r2

n   Any point (x,y) on the boundary of the circle satisfies the equation and circle function is zero

Midpoint Circle Algorithm

n    For a point in the interior of the circle, the circle function is negative and for a point outside the circle, the function is positive

n    Thus,

n   fcircle(x,y) < 0 if (x,y) is inside the circle boundary

n   fcircle(x,y) = 0 if (x,y) is on the circle boundary

n   fcircle(x,y) > 0 if (x,y) is outside the circle boundary

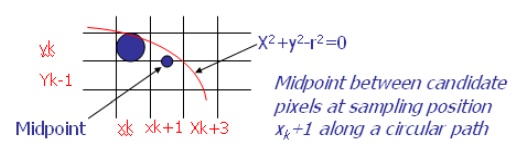
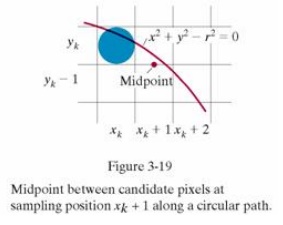
n    Assuming we have just plotted the pixel at (xk,yk) , we next need to determine whether the pixel at position (xk + 1, yk-1) is closer to the circle

n    Our decision parameter is the circle function evaluated at the midpoint between these two pixels

pk = fcircle (xk +1, yk-1/2) = (xk +1)2 + (yk -1/2)2 – r2

If pk < 0 , this midpoint is inside the circle and the pixel on the scan line yk is closer to the circle boundary. Otherwise, the

mid position is outside or on the circle boundary, and we select the pixel on the scan line yk-1

n   Successive decision parameters are obtained using incremental calculations

Pk+1 = fcircle(xk+1+1, yk+1-1/2)

= [(xk+1)+1]2 + (yk+1 -1/2)2 –r2

OR

Pk+1 = Pk+2(xK+1) + (yK+12 – yk2) – (yk+1- yk)+1

Where yk+1 is either yk or yk-1, depending on the sign of pk

n    Increments for obtaining Pk+1:

2xk+1+1 if pk is negative 2xk+1+1-2yk+1 otherwise

n    Note that following can also be done incrementally:

2xk+1 = 2xk +2

2 yk+1 = 2yk – 2

n    At the start position (0,r) , these two terms have the values 2 and 2r-2 respectively

n    Initial decision parameter is obtained by evaluating the circle function at the start position

(x0,y0) = (0,r)

p0 = fcircle(1, r-1/2) = 1+ (r-1/2)2-r2

OR

P0 = 5/4 -r

n   If radius r is specified as an integer, we can round p0 to

p0 = 1-r

The actual algorithm

1:    Input radius r and circle center (xc,yc) and obtain the first point on the circumference of the circle centered on the origin as

(x0,y0) = (0,r)

2:   Calculate the initial value of the decision parameter as

P0 = 5/4 - r

3: At each xk position starting at k = 0 , perform the following test:

If pk < 0 , the next point along the circle centered on (0,0) is (xk+1, yk) and pk+1 = pk + 2xk+1 + 1

Otherwise the next point along the circle is (xk+1, yk-1) and pk+1 = pk + 2xk+1 +1 -2yk+1

Where 2xk+1 = 2xk+2 and 2yk+1 = 2yk-2

4:   Determine symmetry points in the other seven octants

5:      Move each calculated pixel position (x,y) onto the circular path centered on (x,yc) and plot the coordinate values

x = x+ xc   ,         y= y+ yc

6: Repeat steps 3 through 5 until x >= y

ELLIPSE-GENERATING ALGORITHMS

Properties of Ellipses

An ellipse is defined as the set of points such that the sum of the distances from two fixed positions (foci) is the same for all points (Fig. b17).

If the distances to the two foci from any point P = (x, y) on the ellipse are labeled dl and d2, then the general equation of an ellipse can be stated as

d, + d, = constant (3-32)

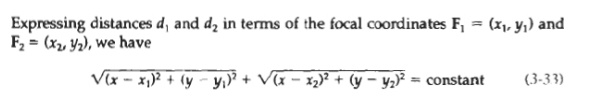
By squaring this equation, isolating the remaining radical, and then squaring again,

we can rewrite the general ellipse equation in the form

Ax2 + By2 + Cxy + Dx + Ey + F = 0 (3-34)

where the coefficients A, B, C, D, E, and F are evaluated l in terms of the focal coordinates and the dimensions of the major and minor axes of the ellipse.

The major axis is the straight line segment extending from one side of the ellipse to the

other through the foci.The minor axis spans the shorter dimension of the ellipse, bisecting the major axis at the halfway position (ellipse center) between the twofoci.An interactive method for specifying an ellipse in an arbitrary orientation is to input the two foci and a point on the ellipse boundary.

With these three coordinate positions, we can evaluate the constant in Eq. 3.33.

Then, the coefficients inEq. 3-34 can be evaluated and used to generate pixels along the ellipticalpath.

Using polar coordinates r and 0. we can also describe the ellipse in standard position with the parametric equations: