Total Probability of an event

Total Probability of an event

Theorem 12.10 (Total Probability of an event)

If A1 , A2 , A3 , ..., An are mutually exclusive and exhaustive events and B is any event in S then P(B) is called the total probability of event B and

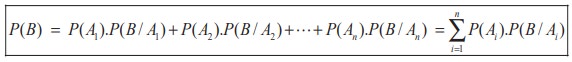
Proof

Since B is any event in S, from the figure shown here

B= ( A1 ∩ B) ∪ ( A2 ∩ B) ∪ ( A3 ∩ B) ∪ ...( An ∩ B).

Since A1 , A2 , A3 ... An  are mutually exclusive,

A1 ∩ B ) , ( A2 ∩ B ) , ( A3 ∩ B ) ,...,( An ∩ B) are also mutually exclusive.

Therefore

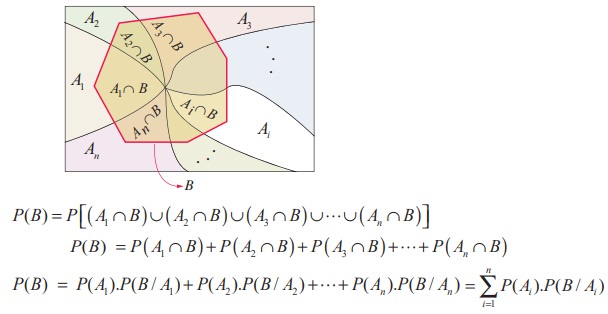
The following problems are solved using the law of total probability of an event.

Example 12.24

Urn-I contains 8 red and 4 blue balls and urn-II contains 5 red and 10 blue balls. One urn is chosen at random and two balls are drawn from it. Find the probability that both balls are red.

Solution

Let A1 be the event of selecting urn-I and A2 be the event of selecting urn-II.

Let B be the event of selecting 2 red balls.

We have to find the total probability of event B . That is, P(B).

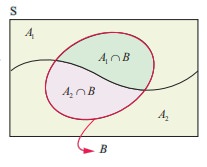
Clearly A1 and A2 A1 are mutually exclusive and exhaustive events.

Example 12.25

A factory has two machines I and II. Machine-I produces 40% of items of the output and Machine-II produces 60% of the items. Further 4% of items produced by Machine-I are defective and 5% produced by Machine-II are defective. If an item is drawn at random, find the probability that it is a defective item.

Solution

Let A1 be the event that the items are produced by Machine-I,   A2 be the event that items are produced by Machine-II. Let B be  the event of drawing a defective item.

We have to find the total probability of event B . That is, P(B).

Clearly A1 and A2 are mutually exclusive and exhaustive events.

Therefore, P(B) = P (A1 ) . P (B / A1 ) + P (A2 ) . P (B / A2 )

We have P (A1 ) = 0.40, P (B / A1 ) = 0.04

P (A2 ) = 0.60, P (B / A2 ) =0.05

P(B) = P (A1 ) . P (B / A1 ) + P (A2 ) . P (B / A2 )

=( 0.40) ( 0.04) + ( 0.60 )( 0.05)

=0.046.