Theorem, Proof, Solved Example Problems | Mathematics - Bayes’ Theorem | 11th Mathematics : UNIT 12 : Introduction to Probability Theory
Chapter: 11th Mathematics : UNIT 12 : Introduction to Probability Theory
Bayes’ Theorem
Bayes’ Theorem
Thomas Bayes was an English statistician, philosopher and Presbyterian minister who is known for formulating a specific case of a theorem. Bayesian methods stem from the principle of linking prior (before conducting experiment) probability and conditional probability (likelihood) to posterior (after conducting experiment) probability via Bayes’ rule. Bayesian probability is the name given to several related interpretations of probability as an amount of epistemic confidence – the strength of beliefs, hypotheses etc., rather than a frequency.
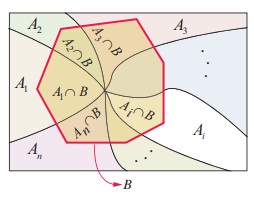

Theorem 12.11 (Bayes’ Theorem)
If A1 , A2 , A3 , ..., An are mutually exclusive and exhaustive events such that P(Ai) > 0, i = 1,2,3,….n and B is any event in which P(B) > 0, then

Proof
By the law of total probability of B we have
P ( B) = P ( A1 ) . P ( B / A1 ) + P( A2 ) . P(B / A2 )+...+P ( An ) P ( B / An ) and by multiplication theorem P ( Ai ‚à© B) = P ( B /Ai ) P ( Ai )
By the definition of conditional probability,

The above formula gives the relationship between P( Ai / B) and P (B / Ai )
Example 12.26
A factory has two machines I and II. Machine I produces 40% of items of the output and Machine II produces 60% of the items. Further 4% of items produced by Machine I are defective and 5% produced by Machine II are defective. An item is drawn at random. If the drawn item is defective, find the probability that it was produced by Machine II. (See the previous example, compare the questions).
Solution
Let A1 be the event that the items are produced by Machine-I, A2 be the event that items are produced by Machine-II. Let B be the event of drawing a defective item. Now we are asked to find the conditional probability P (A2 / B). Since A1 , A2 are mutually exclusive and exhaustive events, by Bayes’ theorem,
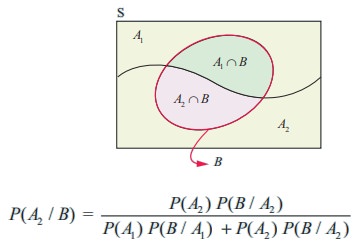
We have,
P ( A1 ) =0.40 , P ( B / A1 ) = 0.04
P ( A2 ) = 0.60, P (B / A2 ) = 0.05

Example 12.27
A construction company employs 2 executive engineers. Engineer-1 does the work for 60% of jobs of the company. Engineer-2 does the work for 40% of jobs of the company. It is known from the past experience that the probability of an error when engineer-1 does the work is 0.03, whereas the probability of an error in the work of engineer-2 is 0.04. Suppose a serious error occurs in the work, which engineer would you guess did the work?
Solution
Let A1and A2 be the events of job done by engineer-1 and engineer-2 of the company respectively. Let B be the event that the error occurs in the work.
We have to find the conditional probability
P (A1 / B ) and P (A2 / B) to compare their errors in their work.
From the given information, we have
P (A1 ) = 0.60, P (B / A1 ) = 0.03
P (A2 ) = 0.40, P (B / A2 ) = 0.04
A1 and A2 are mutually exclusive and exhaustive events.
Applying Bayes’ theorem,
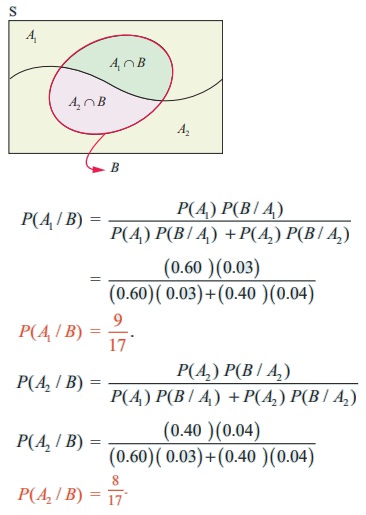
Since P (A1 / B ) > P (A2 / B) , the chance of error done by engineer-1 is greater than the chance of error done by engineer-2. Therefore one may guess that the serious error would have been be done by engineer-1.
Example 12.28
The chances of X, Y and Z becoming managers of a certain company are 4 : 2 : 3. The probabilities that bonus scheme will be introduced if X, Y and Z become managers are 0.3, 0.5 and 0.4 respectively. If the bonus scheme has been introduced, what is the probability that Z was appointed as the manager?
Solution
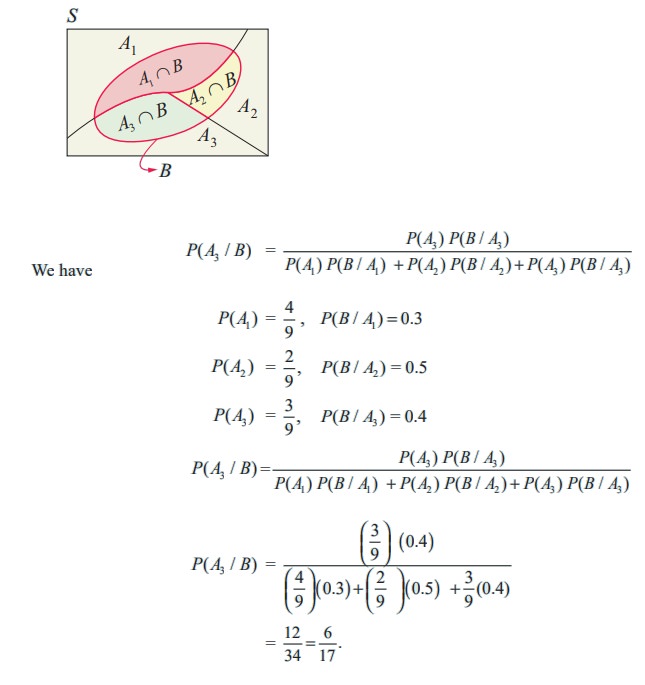
Let A1, A2 and A3 be the events of X, Y and Z becoming managers of the company respectively. Let B be the event that the bonus scheme will be introduced.
We have to find the conditional probability P ( A3 / B).
Since A1 , A2 and A3 are mutually exclusive and exhaustive events, applying Bayes’ theorem
Example 12.29
A consulting firm rents car from three agencies such that 50% from agency L, 30% from agency M and 20% from agency N. If 90% of the cars from L, 70% of cars from M and 60% of the cars from N are in good conditions (i) what is the probability that the firm will get a car in good condition? (ii) if a car is in good condition, what is probability that it has come from agency N?
Solution
Let A1 , A2 , and A3 be the events that the cars are rented from the agencies X, Y and Z respectively.
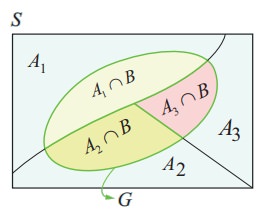
Let G be the event of getting a car in good condition.
We have to find
(i) the total probability of event G that is, P(G)
(ii) find the conditional probability A3 given G that is, P ( A3 / G) We have
P ( A1 ) = 0.50, P (G / A1) = 0.90
P ( A2 ) = 0.30, P (G / A2 ) = 0.70
P (A3 ) = 0.20, P (G / A3 ) = 0.60.
(i) Since A1 , A2 and A3 are mutually exclusive and exhaustive events and G is an event in S, then the total probability of event G is P(G).
P (G) = P (A1 ) P (G / A1 ) + P (A2 ) P (G / A2 ) + P (A3 ) P (G / A3 )
P(G) = ( 0.50)( 0.90) + ( 0.30)( 0.70) + ( 0.20)( 0.60)
P(G) = 0.78.
(ii) The conditional probability A3 given G is P (A3 / G)
By Bayes’ theorem,

EXERCISE 12.4
(1) A factory has two Machines-I and II. Machine-I produces 60% of items and Machine-II produces 40% of the items of the total output. Further 2% of the items produced by Machine-I are defective whereas 4% produced by Machine-II are defective. If an item is drawn at random what is the probability that it is defective?
(2) There are two identical urns containing respectively 6 black and 4 red balls, 2 black and 2 red balls. An urn is chosen at random and a ball is drawn from it. (i) find the probability that the ball is black (ii) if the ball is black, what is the probability that it is from the first urn?
(3) A firm manufactures PVC pipes in three plants viz, X, Y and Z. The daily production volumes from the three firms X, Y and Z are respectively 2000 units, 3000 units and 5000 units. It is known from the past experience that 3% of the output from plant X, 4% from plant Y and 2% from plant Z are defective. A pipe is selected at random from a day’s total production,
(i) find the probability that the selected pipe is a defective one.
(ii) if the selected pipe is a defective, then what is the probability that it was produced by plant Y ?
(4) The chances of A, B and C becoming manager of a certain company are 5 : 3 : 2. The probabilities that the office canteen will be improved i f A, B, and C become managers are 0.4, 0.5 and 0.3 respectively. If the office canteen has been improved, what is the probability that B was appointed as the manager?
(5) An advertising executive is studying television viewing habits of married men and women during prime time hours. Based on the past viewing records he has determined that during prime time wives are watching television 60% of the time. It has also been determined that when the wife is watching television, 40% of the time the husband is also watching. When the wife is not watching the television, 30% of the time the husband is watching the television. Find the probability that (i) the husband is watching the television during the prime time of television (ii) if the husband is watching the television, the wife is also watching the television.
Exercise 12.4
Answers
(1) 0.028
(2) (i) 11/20
(ii) 6/11
(3) (i) 7/250 (ii) 3/7
(4) 15/41
(5) (i) 9/25 (ii) 2/3
Related Topics