Introduction to Probability Theory | Mathematics - Exercise 12.5: Choose the correct answer | 11th Mathematics : UNIT 12 : Introduction to Probability Theory
Chapter: 11th Mathematics : UNIT 12 : Introduction to Probability Theory
Exercise 12.5: Choose the correct answer
Introduction to Probability Theory (Mathematics)
Choose the correct or
most suitable answer from the given four alternatives
(1) Four persons are
selected at random from a group of 3 men, 2 women and 4 children. The
probability that exactly two of them are children is
(1) 3/4
(2) 10/23
(3) 1/2
(4) 10/21
Ans: (4)
Solution

(2) A number is selected
from the set { 1, 2, 3,..., 20 }. The probability that the selected number is
divisible by 3 or 4 is
(1) 2/5
(2) 1/8
(3) 1/2
(4) 2/3
Ans: (3)
Solution

(3) A, B, and C try to
hit a target simultaneously but independently. Their respective probabilities
of hitting the target are 3/4 , 1/2 , 8/5 . The probability that the target is
hit by A or B but not by C is
(1) 21 /64
(2) 7/32
(3) 9/64
(4) 7/8
Ans: (1)
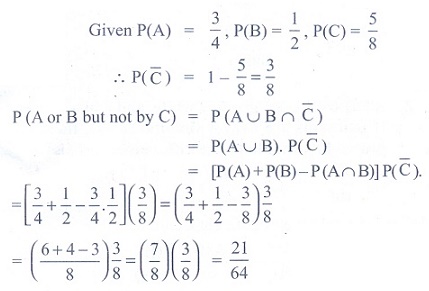
(4) If A and B are any
two events, then the probability that exactly one of them occur is
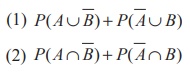
(3) P( A ) + P( B ) ŌłÆ P(
A Ōł® B )
(4) P ( A) + P ( B ) + 2
P ( A Ōł® B)
Ans: (2)
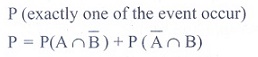
(5) Let A and B be two
events such that P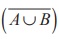 = 1/6 , P ( A Ōł® B) = 1/4 and P (
= 1/6 , P ( A Ōł® B) = 1/4 and P (![]() ) = 1/4 .
Then the events A and B are
) = 1/4 .
Then the events A and B are
(1) Equally likely
but not independent
(2) Independent but not
equally likely
(3) Independent
and equally likely
(4) Mutually inclusive
and dependent
Ans: (2)

(6) Two items are chosen
from a lot containing twelve items of which four are defective, then the
probability that at least one of the item is defective
(1) 19/33
(2) 17/33
(3) 23/33
(4) 13/33
Ans: (1)
Solution

(7) A man has 3 fifty
rupee notes, 4 hundred rupees notes and 6 five hundred rupees notes in his
pocket. If 2 notes are taken at random, what are the odds in favour of both
notes being of hundred rupee denomination?
(1) 1:12
(2) 12:1
(3) 13:1
(4) 1:13
Ans: (1)
Solution

(8) A letter is taken at
random from the letters of the word ŌĆśASSISTANTŌĆÖ and another letter is taken at
random from the letters of the word ŌĆśSTATISTICSŌĆÖ. The probability that the
selected letters are the same is
(1) 7/45
(2) 17/90
(3) 29/90
(4) 19/90
Ans: (4)
Solution

(9) A matrix is chosen
at random from a set of all matrices of order 2, with elements 0 or 1 only. The
probability that the determinant of the matrix chosen is non zero will be
(1) 3/16
(2) 3/8
(3) 1/4
(4) 5/8
Ans: (2)
Solution
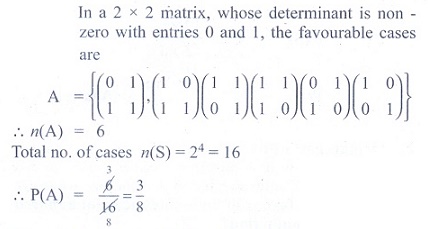
(10) A bag contains 5
white and 3 black balls. Five balls are drawn successively without replacement.
The probability that they are alternately of different colours is
(1) 3/14
(2) 5/14
(3) 1/14
(4) 9/14
Ans: (3)
Solution
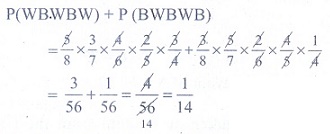
(11) If A and B
are two events such that A ŌŖé B and P (B) ŌēĀ0, then
which of the following is correct?
(1) P ( A / B) = P ( A)
/ P ( B)
(2) P ( A / B ) < P(
A)
(3) P ( A / B ) Ōēź P(
A)
(4) P ( A / B ) >
P(B)
Ans: (3)
(12) A bag
contains 6 green, 2 white, and 7 black balls. If two balls are drawn
simultaneously, then the probability that both are different colours is
(1) 68/105
(2) 71/105
(3) 64/105
(4) 73/105
Ans: (1)
Solution

(13) If X and Y
be two events such that P ( X / Y ) = 1/2 , P ( Y / X ) = 1/3 and P ( X Ōł® Y ) =
16 , then P ( X Ōł¬Y ) is
(1) 1/3
(2) 2/5
(3) 1/6
(4) 2/3
Ans: (4)
Solution
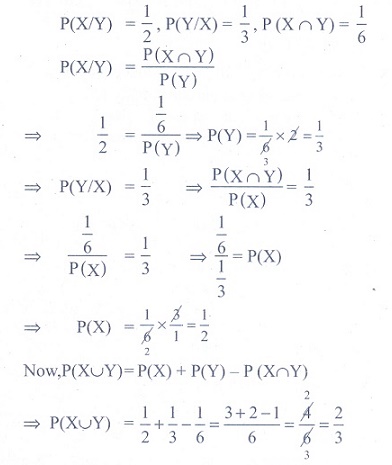
(14) An urn contains 5
red and 5 black balls. A ball is drawn at random, its colour is noted and is
returned to the urn. Moreover, 2 additional balls of the colour drawn are put
in the urn and then a ball is drawn at random. The probability that the second
ball drawn is red will be
(1) 5/12
(2) 1/2
(3) 7/12
(4) 1/4
Ans: (2)
Solution

(15) A number x is
chosen at random from the first 100 natural numbers. Let A be the event
of numbers which satisfies [(x ŌłÆ 10)(x ŌłÆ 50)] / [x ŌłÆ 30 ] Ōēź 0 , then P ( A) is
(1) 0.20
(2) 0.51
(3) 0.71
(4) 0.70
Ans: (3)
Solution

(16) If two events A and
B are independent such that P ( A) = 0.35 and P ( A Ōł¬
B) = 0.6 , then P (B) is
(1) 5/13
(2) 1/13
(3) 4/13
(4) 7/13
Ans: (1)

(17) If two events A
and B are such that P (![]() ) = 3/10 and P ( A Ōł®
) = 3/10 and P ( A Ōł® ![]() ) = 1/2 , then
P ( A Ōł® B) is
) = 1/2 , then
P ( A Ōł® B) is
(1) 1/2
(2) 1/3
(3) 1/4
(4) 1/5
Ans: (4)
Solution
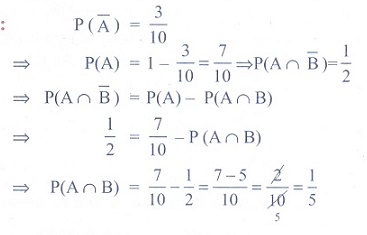
(18) If A and B are two
events such that P (A)= 0.4, P ( B) = 0.8 and P ( B / A) = 0.6 , then P (![]() Ōł® B) is
Ōł® B) is
(1) 0.96
(2) 0.24
(3) 0.56
(4) 0.66
Ans: (3)
Solution

(19) There are three
events A, B and C of which one and only one can happen. If the
odds are 7 to 4 against A and 5 to 3 against B, then odds against C
is
(1) 23: 65
(2) 65: 23
(3) 23: 88
(4) 88: 23
Ans: (2)
Solution

(20) If a and b are
chosen randomly from the set {1,2,3,4}with replacement, then the probability of
the real roots of the equation x2 + ax + b = 0 is
(1) 3/16
(2) 5/16
(3) 7/16
(4) 11/16
Ans: (3)
Solution

(21) It is given that
the events A and B are such that P( A) = 1/4 , P ( A / B) = 1/2 and P ( B / A)
= 2/3 . Then P(B) is
(1) 1/6
(2) 1/3
(3) 2/3
(4) 1/2
Ans: (2)
Solution
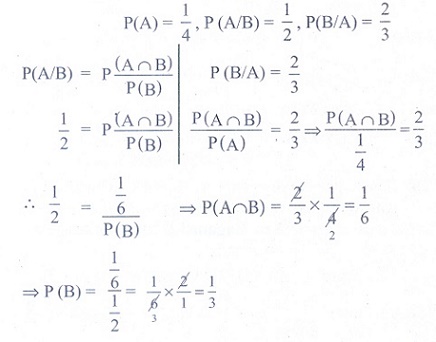
(22) In a certain
college 4% of the boys and 1% of the girls are taller than 1.8 meter. Further
60% of the students are girls. If a student is selected at random and is taller
than 1.8 meters, then the probability that the student is a girl is
(1) 2/11
(2) 3/11
(3) 5/11
(4) 7/11
Ans: (2)
Solution

(23) Ten coins are
tossed. The probability of getting at least 8 heads is
(1) 7/64
(2) 7/32
(3) 7/16
(4) 7/128
Ans: (4)
Solution
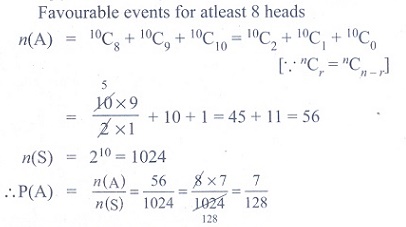
(24) The
probability of two events A and B are 0.3 and 0.6 respectively. The probability
that both A and B occur simultaneously is 0.18. The probability that neither A
nor B occurs is
(1) 0.1
(2) 0.72
(3) 0.42
(4) 0.28
Ans: (4)
Solution

(25) If m is a
number such that m Ōēż 5, then the probability that quadratic equation 2x2
+ 2mx + m + 1 = 0 has real roots is
(1) 1/5
(2) 2/5
(3) 3/5
(4) 4/5
Ans: (3)
Solution
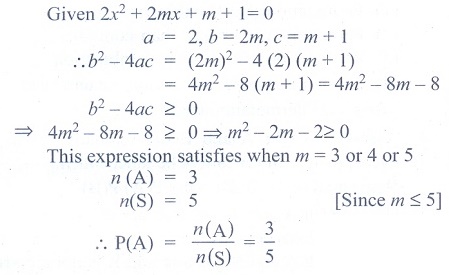
Related Topics