Finite sample space - Probability Theory

Finite sample space

In this section we restrict our sample spaces that have at most a finite number of points.

Types of events

Let us now define some of the important types of events, which are used frequently in this chapter.

• Sure event or certain event

• Complementary event

• Mutually inclusive event

• Equally likely events

• Impossible event

• Impossible event

• Mutually exclusive events

• Exhaustive events

• Independent events (defined after learning the concepts of probability)

Definition 12.6

When the sample space is finite, any subset of the sample space is an event. That is, all elements of the power set P ( S )of the sample space are defined as events. An event is a collection of sample points or elementary events.

The sample space S is called sure event or certain event. The null set ∅ in S is called an impossible event.

Definition 12.7

For every event A, there corresponds another event is called the complementary event to A. It is also called the event ‘not A’.

Illustration 12.2

Suppose a sample space S is given by S = {1,2,3,4}.

Let the set of all possible subsets of S (the power set of S) be P ( S).

P (S) = {∅, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4},{1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}}

(i) All the elements of P ( S ) are events.

(ii) ∅ is an impossible event.

(iii) {1},{2},{3},{4} are the simple events or elementary events.

(iv) {1, 2, 3, 4}is a sure event or certain event.

Definition 12.8

Two events cannot occur simultaneously are mutually exclusive events. A1 , A2 , A3 ,..., Ak are mutually exclusive or disjoint events means that, Ai ∩ Aj = ∅ , for i ≠j.

Definition 12.9

Two events are mutually inclusive when they can both occur simultaneously.

A1 , A2 , A3 ,..., Ak  are mutually inclusive means that, Ai ∩ Aj ≠ ∅ , for i ≠ j

Illustration 12.3

When we roll a die, the sample space S = {1,2,3,4,5,6}.

(i) Since{1, 3}∩ {2, 4, 5, 6}=∅, the events {1,3}and{2, 4,5,6}are mutually exclusive events.

(ii) The events {1,6,},{2,3,5} are mutually exclusive.

(iii) The events {2,3,5},{5,6} are mutually inclusive, since {2, 3, 5}∩ {5, 6}={5} ≠ ∅

Definition 12.10

A1 , A2 , A3 ,..., Ak  are called exhaustive events if, A1 ∪ A2 ∪ A3 ∪ .... ∪ Ak  = S

Definition 12.11

A1 , A2 , A3 ,..., Ak  are called mutually exclusive and exhaustive events if,

(i) Ai∩ Aj  â‰ âˆ… , for i ≠ j

(ii) A1 ∪ A2  âˆª A3 ∪ ........ ∪ Ak = S

Illustration 12.4

When a die is rolled, sample space S = {1,2,3,4,5,6}.

Some of the events are {2,3},{1,3,5},{4,6},{6} and{1,5}.

(i) Since {2, 3}∪ {1, 3, 5}∪{4, 6} = {1, 2, 3, 4, 5, 6} = S (sample space), the events {2,3},{1,3,5},{4,6} are exhaustive events.

(ii) Similarly {2,3},{4,6}and{1,5} are also exhaustive events.

(iii) {1,3,5},{4,6},{6} and{1,5} are not exhaustive events.

(Since {1, 3, 5}∪ {4, 6}∪ {6}∪ {1, 5} ≠ S)

(iv){2,3},{4,6},and{1,5} are mutually exclusive and exhaustive events, since

{2,3}∩{4, 6} = ∅, {2, 3}∩{1, 5}= ∅,{4, 6}∩{1, 5} = ∅ and {2, 3}∪ {4, 6}∪ {1, 5} = S

Types of events associated with sample space are easy to visualize in terms of Venn diagrams, as illustrated below.

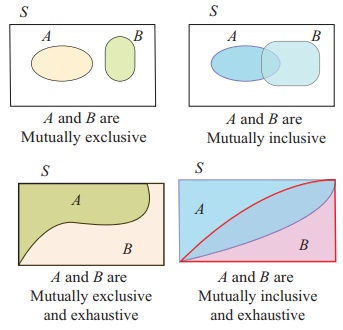
Definition 12.12

The events having the same chance of occurrences are called equally likely events.

Example for equally likely events: Suppose a fair die is rolled.

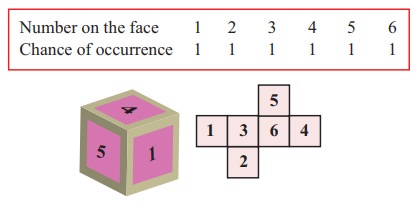
Example for not equally likely events: A colour die is shown in figure is rolled.

Similarly, suppose if we toss a coin, the events of getting a head or a tail are equally likely.

Methods to find sample space

Illustration 12.5

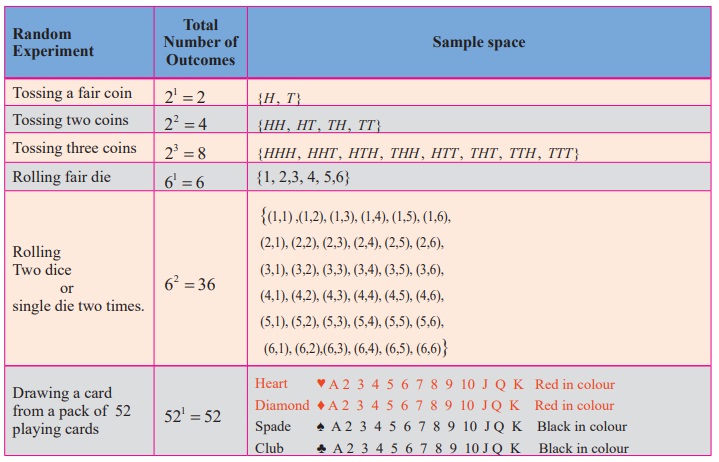
Two coins are tossed, the sample space is

(i) S = {H ,T }× {H ,T } = {(H , H ),(H ,T ),(T , H ),(T ,T )} or {HH , HT ,TH ,TT}

(ii) If a coin is tossed and a die is rolled simultaneously, then the sample space is

S= {H ,T}×{1,2,3,4,5,6} = {H 1, H 2, H 3, H 4, H 5, H 6,T 1,T 2,T 3,T 4,T 5,T 6} or

S= {(H ,1),(H ,2),(H ,3),(H ,4),(H ,5),(H ,6),(T ,1),(T ,2),(T ,3),(T ,4),(T ,5),(T ,6)}.

Also one can interchange the order of outcomes of coin and die. The following table gives the sample spaces for some random experiments.

Notations

Let A and B be two events.

(i) A ∪ B stands for the occurrence of A or B or both.

(ii) A ∩ B stands for the simultaneous occurrence of A and B. A ∩ B can also be written as AB

(iii) or A′ or Ac stands for non-occurrence of A

(iv) A ∩ stands for the occurrence of only A.