Chapter: 11th Mathematics : UNIT 12 : Introduction to Probability Theory
Some basic Theorems on Probability
Some basic Theorems on Probability
The problems solved in the last sections are related to mutually exclusive events. So we have used the formula P ( A or B ) = P ( A ‚ą™ B) = P ( A) + P (B) . But when the events are mutually inclusive, the additivity axioms counts ( A ‚ą© B) twice. We have a separate formula for the events when they are mutually inclusive.
In the development of probability theory, all the results are derived directly or indirectly using only the axioms of probability. Here we derive some of the basic important theorems on probability.
Theorem 12.3
The probability of the impossible event is zero. That is,
P(‚ąÖ ) = 0
Proof
Impossible event contains no sample point.
Therefore, S ‚ą™ ‚ąÖ = S
P(S ‚ą™ ‚ąÖ) = P(S)
P(S) P(‚ąÖ) = P (S) (since S and ‚ąÖ are mutually exclusive)
P(‚ąÖ) = 0
Example 12.12
Find the probability of getting the number 7, when a usual die is rolled.
Solution
The event of getting 7 is an impossible event. Thereforee, P (getting 7) = 0
Theorem 12.4

Example 12.13
Nine coins are tossed once, find the probability to get at least two heads.
Solution
Let S be the sample space and A be the event of getting at least two heads.
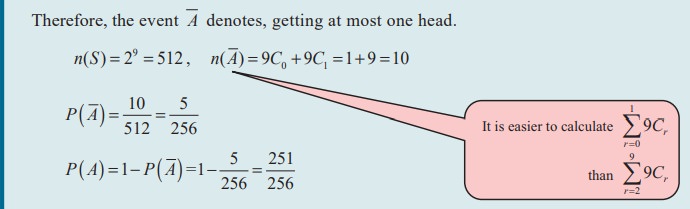
Theorem 12.5

Theorem 12.6 (Addition theorem on probability)
If A and B are any two events, then
P ( A ‚ą™ B ) = P ( A) + P ( B ) ‚ąí P ( A ‚ą© B)
Proof
From the diagram,

[ P ( A) ‚ąí P ( A ‚ą© B )] + P ( B)
Therefore, P ( A ‚ą™ B) = P ( A) + P ( B ) ‚ąí P ( A ‚ą© B)
Note 12.4
The above theorem can be extended to any 3 events.
(i) P ( A ‚ą™ B ‚ą™ C) ={ P ( A) + P ( B ) + P (C)} - {P ( A ‚ą© B ) + P (B ‚ą© C ) + P (C ‚ą© A)}+ P ( A ‚ą© B ‚ą© C)}
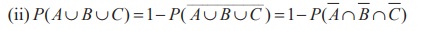

Example 12.15
The probability that a girl, preparing for competitive examination will get a State Government service is 0.12, the probability that she will get a Central Government job is 0.25, and the probability that she will get both is 0.07. Find the probability that (i) she will get atleast one of the two jobs (ii) she will get only one of the two jobs.
Solution
Let I be the event of getting State Government service and C be the event of getting Central Government job.
Given that P(I) = 0.12, P(C) = 0.25, and P ( I ‚ą© C) = 0.07
(i) P (at least one of the two jobs) = P (I or C ) = P (I ‚ą™ C)
= P (I ) + P (C ) ‚ąí P (I ‚ą© C)
= 0.12 + 0.25 ‚ąí 0.07 = 0.30
(ii) P(only one of the two jobs) = P[only I or only C].
= 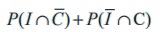
= {P (I ) ‚ąí P (I ‚ą© C )}+ {P (C ) ‚ąí P (I ‚ą© C)}
= {0.12 ‚ąí 0.07} + {0.25 ‚ąí 0.07}
= 0.23.
EXERCISE 12.2
(1) If A and B are mutually exclusive events P ( A) = 3/8 and P (B) = 1/8 , then
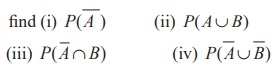
(2) If A and B are two events associated with a random experiment for which P (A) = 0.35, P ( A or B) = 0.85, and P ( A and B) = 0.15.
Find (i) P (only B) (ii) P ( ![]() ) (iii) P (only A)
) (iii) P (only A)
(3) A die is thrown twice. Let A be the event, ‚ÄėFirst die shows 5‚Äô and B be the event, ‚Äėsecond die shows 5‚Äô. Find P( A ‚ą™ B) .
(4) The probability of an event A occurring is 0.5 and B occurring is 0.3. If A and B are mutually exclusive events, then find the probability of
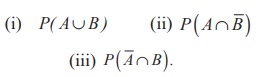
(5) A town has 2 fire engines operating independently. The probability that a fire engine is available when needed is 0.96.
(i) What is the probability that a fire engine is available when needed?
(ii) What is the probability that neither is available when needed?
(6) The probability that a new railway bridge will get an award for its design is 0.48, the probability that it will get an award for the efficient use of materials is 0.36, and that it will get both awards is 0.2. What is the probability, that (i) it will get at least one of the two awards ( ii) it will get only one of the awards.
Answers Exercise 12.2 (1) (i) 5/8 (ii) 1/2 (iii)) 1/8 (iv) 1 (2) (i) 0.50 (ii) 0.35 (iii) 0.20 (3) 11/36 (4) (i) 0.8 (ii) 0.5 (iii) 0.3 (5) (i) 0.9984 (ii) 0.0016
(6) (i) 0.64 (ii) 0.44
Related Topics