Theorem, Solved Example Problems - Axiomatic approach to Probability | 11th Mathematics : UNIT 12 : Introduction to Probability Theory
Chapter: 11th Mathematics : UNIT 12 : Introduction to Probability Theory
Axiomatic approach to Probability
Axiomatic approach to Probability
Axioms of probability
Let S be a finite sample space, let P ( S) be the class of events, and let P be a real valued function defined on P ( S) Then P ( A) is called probability function of the event A , when the following axioms are hold:
[P1 ] For any event A, P ( A) Ōēź 0 (Non-negativity axiom)
[P2 ] For any two mutually exclusive events P ( A Ōł¬ B ) = P ( A) + P (B) (Additivity axiom)
[P3 ] For the certain event P (S) = 1 (Normalization axiom)
Note 12.1
(i) 0 Ōēż P ( A) Ōēż 1
(ii) If A1 , A2 , A3 ,..., An are mutually exclusive events in a sample space S, then P (A1 Ōł¬ A2 Ōł¬ A3 Ōł¬ŌĆ”Ōł¬ An ) = P ( A1 ) + P ( A2 ) + P ( A3 ) +ŌĆ”+P(An)
Theorems on finite probability spaces (without proof)
When the outcomes are equally likely Theorem 12.1 is applicable, else Theorem 12.2 is applicable.
Theorem 12.1
Let S be a sample space and, for any subset A of S, let P ( A) =n ( A) / n (S). . Then P(A) satisfies axioms of probability [P1 ],[P2 ], and [P3 ] .
Theorem12.2
Let S be a finite sample space say S = {a1 , a2 , a3 ,..., an }. A finite probability space is obtained by assigning to each point ai in S a real number pi , is called the probability of ai , satisfying the following properties:
(i) Each pi Ōēź 0 . (ii) The sum of the pi is 1, that is, Ōłæ pi = p1 + p2 + p3 +...+ p1 = 1.
If the probability P ( A), of an event [P1] is defined as the sum of the probabilities of the points in A , then the function P (A) satisfies the axioms of probability [P1],[P2 ], and [P3] .
Note: Sometimes the points in a finite sample space and their assigned probabilities are given in the form of a table as follows:

Here is an illustration of how to construct a probability law starting from some common sense assumptions about a model.
Illustration 12.6
(1) Let S = {1, 2,3}. Suppose P( S) is the power set of S, and P ( A) = n(A)/n(S).
Then P ({1}) = 1/3 , P ({2}) = 1/3 , and P ({3}) = 1/3 ,
satisfies axioms of probability [P1],[P2], and [P3] . Here all the outcomes are equally likely.
(2) Let S = {1, 2, 3}.Suppose P ( S)is the power set of S ,
If the probability P ( A), of an event[P1] of S is defined as the sum of the probabilities of the points in A ,
then P ({1}) = 1/2 , P ({2}) = 1/4 , P ({3}) = 1/4 ,
satisfy the axioms of probability [P1],[P2], and [P3] .
(3) Let S = {1, 2,3} and P (S) is the power set of S . If the probability P ( A), of an event [P1] of
S is defined as the sum of the probabilities of the points in A ,
then P({ 1}) = 0, P ({2}) = 1/ŌłÜ2 , and P ({3}) = 1ŌłÆ 1/ŌłÜ2 , satisfy the above axioms [P1 ],[P2 ], and [P3 ] .
In (2) and (3), the outcomes are not equally likely.
Note 12.2
Irrational numbers also can act as probabilities.

Example 12.1
If an experiment has exactly the three possible mutually exclusive outcomes A, B, and C, check in each case whether the assignment of probability is permissible.
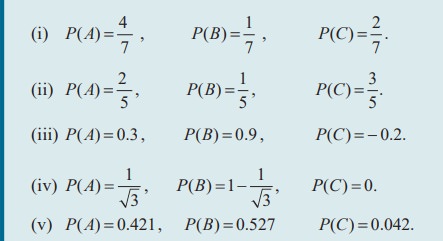
Solution
Since the experiment has exactly the three possible mutually exclusive outcomes A, B and C, they must be exhaustive events.
ŌćÆ S = A Ōł¬ B Ōł¬ C
Therefore, by axioms of probability
P ( A) Ōēź 0, P (B ) Ōēź 0, P (C) Ōēź 0 and
P ( A Ōł¬ B Ōł¬ C ) = P (A) + P ( B ) + P (C) = P (S) = 1

Therefore the assignment is not permissible.
(iii) Since P (C) = ŌłÆ 0.2 is negative, the assignment is not permissible.
(iv) The assignment is permissible because
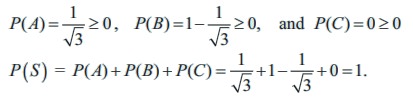
(v) Even though P ( A) = 0.421 Ōēź 0 , P (B) = 0.527 Ōēź 0, and P (C) = 0.042 Ōēź 0 , the sum of the probability
P ( S ) = P (A) + P (B ) + P (C) = 0.421+ 0.527 + 0.042 = 0.990 < 1 .
Therefore, the assignment is not permissible.
Example 12.2
An integer is chosen at random from the first ten positive integers. Find the probability that it is (i) an even number (ii) multiple of three.
Solution
The sample space is
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} , n ( S) = 10
Let A be the event of choosing an even number and B be the event of choosing an integer multiple of three.
A = {2, 4, 6, 8, 10}, n ( A) = 5,
B = {3, 6, 9}, n (B) = 3

Example 12.3
Three coins are tossed simultaneously, what is the probability of getting (i) exactly one head at least one head (iii) at most one head?
Solution:
Notice that three coins are tossed simultaneously = one coin is tossed three times.
The sample space S = { H , T } ├Ś { H , T } ├Ś{H , T}
S= {HHH , HHT , HTH ,THH , HTT ,THT,TTH ,TTT}, n(S) = 8
Let A be the event of getting one head, B be the event of getting at least one head and C be the event of getting at most one head.
A= {HTT,THT,TTH}; n( A) = 3
B= {HTT,THT,TTH , HHT, HTH ,THH , HHH}; n(B) = 7
C= {TTT, HTT,THT,TTH}; n(C) = 4 .
Therefore the required probabilities are
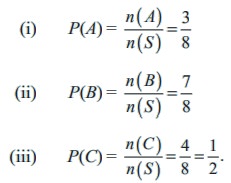
Note 12.3
When the number of elements in sample space is considerably small we can solve by finger-counting the elements in the events. But when the number of elements is too large to count then combinatorics helps us to solve the problems.

For the following problem, combinatorics is used to find the number of elements in the sample space and the events.
Example 12.4
Suppose ten coins are tossed. Find the probability to get (i) exactly two heads (ii) at most two heads (iii) at least two heads
Solution
Ten coins are tossed simultaneously one time = one coin is tossed 10 times
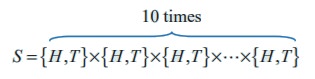
Let
A be the event of getting exactly two heads,
B be the event of getting at most two heads, and
C be the event of getting at least two heads.
When ten coins are tossed, the number of elements in sample space is 2n = 210 =1024
n ( S) = 1024
n ( A) = 10C2 = 45
n ( B ) = 10 C0 +10 C1 +10 C2 = 1 + 10 + 45 = 56
n (C ) = 10 C 2 +10 C3 +10 C 4 +.....+10 C10
=n(S) - (10C0 + 10C1) = 1024 - 11 = 1013
The required probabilities are
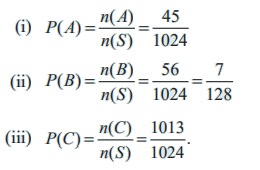
Example 12.5
Suppose a fair die is rolled. Find the probability of getting
(i) an even number (ii) multiple of three.
Solution
Let S be the sample space,
A be the event of getting an even number,
B be the event of getting multiple of three.
Therefore,
S = {1, 2, 3, 4, 5, 6}. ŌćÆ n ( S) = 6
A = {2, 4, 6} ŌćÆ n ( A) = 3
B = {3, 6} ŌćÆ n ( B) = 2
The required probabilities are
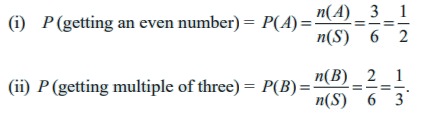
Example 12.6
When a pair of fair dice is rolled, what are the probabilities of getting the sum
(i) 7 (ii) 7 or 9 (iii) 7 or 12?
Solution
The sample space S = {1, 2, 3, 4, 5, 6} ├Ś{1, 2, 3, 4, 5, 6}
= {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6),
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6),
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6),
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6),
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}
Number of possible outcomes = 6 2 = 36 = n ( S)
Let A be the event of getting sum 7, B be the event of getting the sum 9 and C be the event of getting sum 12. Then
A = {(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)} ŌćÆ n ( A) = 6
B = {(3,6),(4,5),(5,4),(6,3)} ŌćÆ n (B) = 4
C = {(6,6)} ŌćÆ n (C) = 1

Example 12.7
Three candidates X, Y, and Z are going to play in a chess competition to win FIDE (World Chess Federation) cup this year. X is thrice as likely to win as Y and Y is twice as likely as to win Z. Find the respective probability of X, Y and Z to win the cup.

Solution
Let A, B, C be the event of winning FIDE cup respectively by X, Y, and Z this year.
Given that X is thrice as likely to win as Y.
A : B : : 3 : 1. (1)
Y is twice as likely as to win Z
B : C : : 2 : 1 (2)
From (1) and (2)
A : B : C : : 6 : 2 : 1
A = 6k, B =2k, C = k,
where k is proportional constant.
Probability to win the cup by X is P ( A) = 6 k/ 9k = 2 /3
Probability to win the cup by Y is P (B) = 2k/ 9k = 2/9 and
Probability to win the cup by Z is P (C) = k/9k = 1/9 .
Example 12.8
Three letters are written to three different persons and addresses on three envelopes are also written. Without looking at the addresses, what is the probability that (i) exactly one letter goes to the right envelopes (ii) none of the letters go into the right envelopes?
Solution
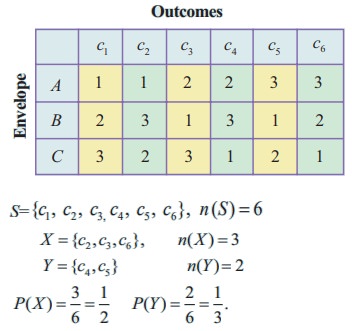
Let A, B, and C denote the envelopes and 1, 2, and 3 denote the corresponding letters.
The different combination of letters put into the envelopes are shown in the table.
Let ci denote the outcomes of the events.
Let X be the event of putting the letters into the exactly only one right envelopes.
Let Y be the event of putting none of the letters into the right envelope.
S={c1 , c2 , c3, c4 , c5 , c6}, n (S) = 6
Example 12.9
Let the matrix 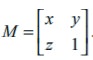 . If x,y and z are chosen at random from the set { 1, 2,3} , and repetition is allowed (i.e., x = y = z ), what is the probability that the given matrix M is a singular matrix?
. If x,y and z are chosen at random from the set { 1, 2,3} , and repetition is allowed (i.e., x = y = z ), what is the probability that the given matrix M is a singular matrix?
Solution
If the given matrix M is singular, then

Hence the possible ways of selecting ( x , y , z) are
{(1,1,1) , ( 2,1, 2 ) , ( 2, 2,1) , ( 3,1,3 ) , ( 3,3,1)} = A ( say)
The number of favourable cases n ( A) = 5
The total number of cases are n ( S) = 33 = 27
The probability of the given matrix is a singular matrix is
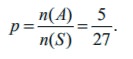
Example 12.10
For a sports meet, a winnersŌĆÖ stand comprising of three wooden blocks is in the form as shown in figure. There are six different colours available to choose from and three of the wooden blocks is to be painted such that no two of them has the same colour. Find the probability that the smallest block is to be painted in red, where red is one of the six colours.
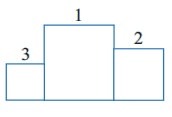
Solution
Let S be the sample space and A be the event that the smallest block is to be painted in red.
n ( S) = 6 P3 = 6 ├Ś 5 ├Ś 4 = 120
n ( A) = 5 ├Ś 4 = 20
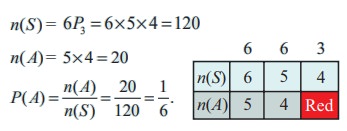
Related Topics