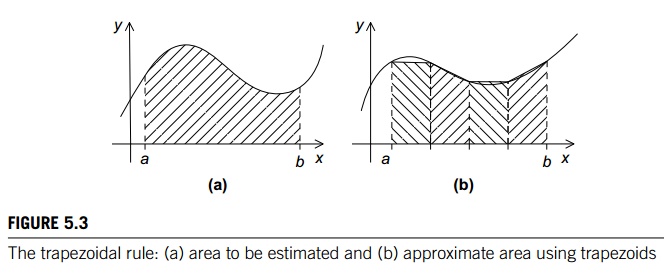
The Trapezoidal Rule

THE TRAPEZOIDAL RULE

Let’s take a look at a somewhat more useful (and more complicated) example: the trapezoidal rule for estimating the area under a curve. Recall from Section 3.2 that if y = f (x) is a reasonably nice function, and a < b are real numbers, then we can estimate the area between the graph of f .x/, the vertical lines x = a and x = b, and the x-axis by dividing the interval [a, b] into n subintervals and approximating the area over each subinterval by the area of a trapezoid. See Figure 5.3 for an example.

Also recall that if each subinterval has the same length and if we define h = (b −a)/n, xi = a + ih, i = 0, 1,...,n, then our approximation will be

h[ f(x₀)/2 + f(x₁) + f(x₂) + ··· + f(x_n−1) + f(x_n)/2].

Thus, we can implement a serial algorithm using the following code:

/* Input: a, b, n */

h = (b-a)/n;

approx = (f(a) + f(b))2/2.0;

for (i = 1; i <= n 1; i++) {

x i = a + i h;

approx += f(x i);

}

approx = h*approx;

See Section 3.2.1 for details.

1. A first OpenMP version

Recall that we applied Foster’s parallel program design methodology to the trapezoidal rule as described in the following list (see Section 3.2.2).

       We identified two types of tasks:

        Computation of the areas of individual trapezoids, and

        Adding the areas of trapezoids.

       There is no communication among the tasks in the first collection, but each task in the first collection communicates with task 1(b).

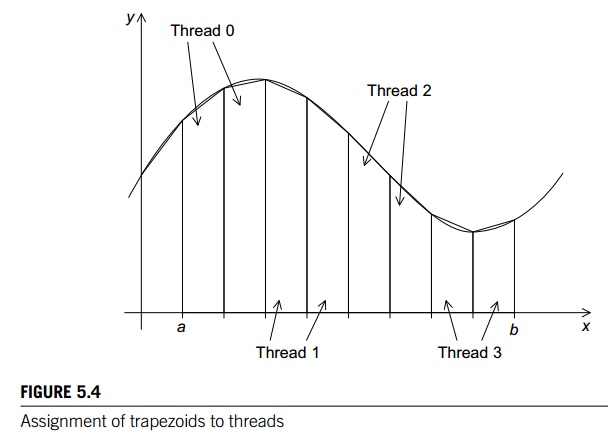
       We assumed that there would be many more trapezoids than cores, so we aggre-

gated tasks by assigning a contiguous block of trapezoids to each thread (and a single thread to each core).² Effectively, this partitioned the interval [a, b] into larger subintervals, and each thread simply applied the serial trapezoidal rule to its subinterval. See Figure 5.4 for an example.

We aren’t quite done, however, since we still need to add up the threads’ results. An obvious solution is to use a shared variable for the sum of all the threads’ results, and each thread can add its (private) result into the shared variable. We would like to have each thread execute a statement that looks something like global_result += my_result;

However, as we’ve already seen, this can result in an erroneous value for global result—if two (or more) threads attempt to simultaneously execute this statement, the result will be unpredictable. For example, suppose that global_result has been initialized to 0, thread 0 has computed my_result = 1, and thread 1 has computed my_result = 2. Furthermore, suppose that the threads execute the statement global_result += my_result according to the following timetable:

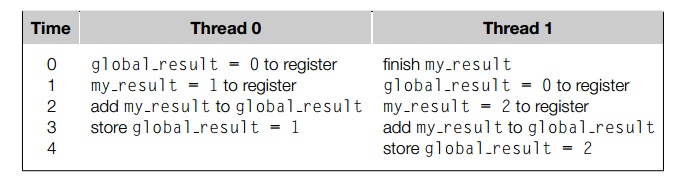
We see that the value computed by thread 0 (my_result = 1) is overwritten by thread 1.

Of course, the actual sequence of events might well be different, but unless one thread finishes the computation global_result += my_result before the other starts, the result will be incorrect. Recall that this is an example of a race condition: multiple threads are attempting to access a shared resource, at least one of the accesses is an update, and the accesses can result in an error. Also recall that the code that causes the race condition, global result += my_result, is called a critical section. A critical section is code executed by multiple threads that updates a shared resource, and the shared resource can only be updated by one thread at a time.

We therefore need some mechanism to make sure that once one thread has started executing global_result += my_result, no other thread can start executing this code until the first thread has finished. In Pthreads we used mutexes or semaphores. In OpenMP we can use the critical directive          pragma omp critical

global_result += my_result;

This directive tells the compiler that the system needs to arrange for the threads to have mutually exclusive access to the following structured block of code. That is, only one thread can execute the following structured block at a time. The code for this version is shown in Program 5.2. We’ve omitted any error checking. We’ve also omitted code for the function f (x).

In the main function, prior to Line 16, the code is single-threaded, and it simply gets the number of threads and the input (a, b, and n). In Line 16 the parallel directive specifies that the Trap function should be executed by thread count threads. After returning from the call to Trap, any new threads that were started by the parallel directive are terminated, and the program resumes execution with only one thread. The one thread prints the result and terminates.

In the Trap function, each thread gets its rank and the total number of threads in the team started by the parallel directive. Then each thread determines the following:

       The length of the bases of the trapezoids (Line 32)

The number of trapezoids assigned to each thread (Line 33)

Program 5.2: First OpenMP trapezoidal rule program

          #include <stdio.h>

          #include <stdlib.h>

          #include <omp.h>

          void Trap(double a, double b, int n, double*  global_result_p);

          int main(int argc, char  argv[]) {

          double         global_result = 0.0;

          double  a, b;

          int     n;

          int     thread_count;

          thread count = strtol(argv[1], NULL, 10);

          printf("Enter a, b, and nnn");

          scanf("%lf %lf %d", &a, &b, &n);

          #  pragma omp parallel num threads(thread count)

          Trap(a, b, n, &global_result);

          printf("With n = %d trapezoids, our estimatenn", n);

          printf("of the integral from %f to %f = %.14enn",

          a, b, global result);

          return 0;

          }  /  main  /

          void Trap(double a, double b, int n, double         global result p) {

          double  h, x, my result;

          double  local_a, local_b;

          int  i, local n;

          int my_rank = omp_get_thread_num();

          int thread_count = omp_get_num_threads();

          h = (b-a)/n;

          local_n = n/thread count;

          local_a = a + my_rank * local_n * h;

          local_b = local_a + local_n*h;

          my result = (f(local a) + f(local b))/2.0;

          for (i = 1; i <= local n 1; i++) f

          x = local_a + i*h;

          my_result += f(x);

          }

          my result = my result h;

          #  pragma omp critical

          *global result_p += my_result;

          }  /*  Trap  */

        The left and right endpoints of its interval (Lines 34 and 35, respectively)

        Its contribution to global result (Lines 36–41)

The threads finish by adding in their individual results to global result in Lines 43 and 44.

We use the prefix local for some variables to emphasize that their values may differ from the values of corresponding variables in the main function—for example, local a may differ from a, although it is the thread’s left endpoint.

Notice that unless n is evenly divisible by thread count, we’ll use fewer than n trapezoids for global result. For example, if n = 14 and thread count = 4, each thread will compute

local n = n/thread count = 14/4 = 3.

Thus each thread will only use 3 trapezoids, and global result will be computed with 4 3 = 12 trapezoids instead of the requested 14. So in the error checking (which isn’t shown) we check that n is evenly divisible by thread count by doing something like this:

if (n % thread count != 0) {

fprintf(stderr, "n must be evenly divisible by thread_countnn");

exit(0);

}

Since each thread is assigned a block of local n trapezoids, the length of each thread’s interval will be local n h, so the left endpoints will be

thread 0: a + 0 local_n*h

thread 1: a + 1 local_n*h

thread 2: a + 2 local_h*h

. . .

and in Line 34, we assign

local_a = a + my_rank local_n*h;

Furthermore, since the length of each thread’s interval will be local n h, its right endpoint will just be

local_b = local_a + local_n*h;