Chapter: An Introduction to Parallel Programming : Shared-Memory Programming with OpenMP
More About Loops in Openmp: Sorting
MORE ABOUT LOOPS IN OPENMP: SORTING
1. Bubble sort
Recollect that the serial bubble sort algorithm for sorting a list of integers can
be implemented as follows:
for (list length = n; list length >= 2; list
length --)
for (i =
0; i < list length-1; i++)
if (a[i] > a[i+1]) {
tmp = a[i];
a[i] = a[i+1];
a[i+1] = tmp;
}
Here, a stores n ints and the algorithm sorts them in increasing
order. The outer loop first finds the largest element in the list and stores it
in a[n 1]; it then finds the next-to-the-largest element and stores it in a[n 2], and so on. So, effectively, the first pass is working with the
full n-element list. The second is working with all
of the elements, except the largest; it’s working with an n 1-element list, and so on.
The inner loop compares consecutive pairs of
elements in the current list. When a pair is out of order (a[i] > a[i+1]) it swaps them. This process of swapping will move the largest
element to the last slot in the “current” list, that is, the list consisting of
the elements
a[0], a[1], . . . , a[list length-1]
It’s pretty clear that there’s a loop-carried
dependence in the outer loop; in any iteration of the outer loop the contents
of the current list depends on the previous iterations of the outer loop. For
example, if at the start of the algorithm a = 3,
4, 1, 2, then the second iteration of the outer loop
should work with the list 3, 1, 2, since the 4 should be moved to the last
position by the first iteration. But if the first two iterations are executing
simultaneously, it’s possible that the effective list for the second iteration
will contain 4.
The loop-carried dependence in the inner loop
is also fairly easy to see. In iter-ation i the elements that are compared depend on the outcome of iteration i- 1. If in iteration i -1, a[i -1] and a[i] are not swapped, then iteration i should compare a[i]
and a[i+1]. If, on the other hand, iteration i -1 swaps a[i -1]
and a[i], then iteration i should be comparing the original a[i -1] (which is now a[i]) and a[i+1]. For example, suppose the current list is {3,1,2}. Then when i = 1, we should com-pare 3 and 2, but if the i = 0 and the i = 1 iterations are happening simultaneously, it’s entirely possible
that the i = 1 iteration will compare 1 and 2.
It’s also not at all clear how we might remove
either loop-carried dependence without completely rewriting the algorithm. It’s
important to keep in mind that even though we can always find loop-carried
dependences, it may be difficult or impos-sible to remove them. The parallel for directive is not a universal solution to the problem of
parallelizing for loops.
2. Odd-even transposition sort
Odd-even transposition sort is a sorting
algorithm that’s similar to bubble sort, but that has considerably more
opportunities for parallelism. Recall from Section 3.7.1 that serial odd-even
transposition sort can be implemented as follows:
for (phase =
0; phase < n; phase++)
if (phase % 2 == 0)
for (i =
1; i < n; i
+= 2)
if (a[i- 1]
> a[i])
Swap(&a[i -1],&a[i]);
else
for (i =
1; i < n- 1;
i += 2)
if (a[i] >
a[i+1]) Swap(&a[i],
&a[i+1]);
The list a stores n ints, and the algorithm sorts them into increasing
order. During an “even phase” (phase % 2 == 0), each odd-subscripted element, a[i], is compared to the element to its “left,” a[i- 1], and if they’re out of order, they’re swapped. During an “odd”
phase, each odd-subscripted element is compared to the element to its right,
and if they’re out of order, they’re swapped. A theorem guarantees that after n phases, the list will be sorted.
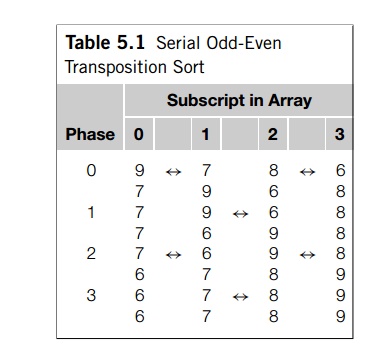
As a brief example, suppose a = {9, 7, 8,
6}. Then the phases are shown in Table 5.1. In
this case, the final phase wasn’t necessary, but the algorithm doesn’t bother
checking whether the list is already sorted before carrying out each phase.
It’s not hard to see that the outer loop has a
loop-carried dependence. As an exam-ple, suppose as before that a = {9, 7, 8,
6}. Then in phase 0 the inner loop will compare elements in the
pairs (9, 7) and (8, 6), and both pairs are swapped. So for phase 1 the list should be {7, 9, 6, 8}, and during phase 1 the elements in the pair (9, 6) should be compared and swapped. However, if phase 0 and phase 1 are executed simultaneously, the pair that’s
checked in phase 1 might be (7, 8), which is in order. Furthermore, it’s not
clear how one might eliminate this loop-carried dependence, so it would appear
that parallelizing the outer for loop isn’t an option.
The inner for loops, however, don’t appear to have any loop-carried
depen-dences. For example, in an even phase loop, variable i will be odd, so for two distinct values of i, say i = j and i = k, the pairs {j -1, j} and {k -1, k} will be be disjoint. The comparison and
possible swaps of the pairs (a[j -1], a[j]) and (a[k -1], a[k]) can therefore proceed simultaneously.
Thus, we could try to parallelize odd-even
transposition sort using the code shown in Program 5.4, but there are a couple
of potential problems. First, although any iteration of, say, one even phase
doesn’t depend on any other iteration of that phase, we’ve already noted that
this is not the case for iterations in phase p and phase p + 1. We need to be sure that all the threads have finished phase p before any thread starts phase p=+ 1. However, like the parallel
directive, the
parallel for directive has an implicit barrier at the end of the loop, so
none of the threads will proceed to the next phase, phase p + 1, until all of the threads have completed the current phase, phase p.
A second potential problem is the overhead
associated with forking and joining the threads. The OpenMP implementation may fork and join thread
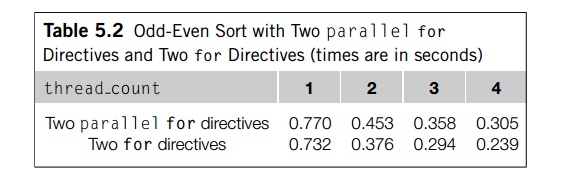
count threads on each pass through the body of the outer loop. The first row of Table
5.2 shows run-times for 1, 2, 3, and 4 threads on one of our systems when the
input list contained 20,000 elements.
Program 5.4: First OpenMP implementation of odd-even sort
for
(phase = 0; phase < n; phase++) {
if
(phase % 2 == 0)
# pragma omp parallel for num
threads(thread count) \
default(none)
shared(a, n) private(i, tmp)
for
(i = 1; i < n; i += 2) {
if
(a[i 1] > a[i]) {
tmp
= a[i-1];
a[i
1] = a[i];
a[i]
= tmp;
}
}
else
#pragma
omp parallel for num threads(thread count) \
default(none)
shared(a, n) private(i, tmp)
for
(i = 1; i < n 1; i += 2) {
if
(a[i] > a[i+1]) {
tmp
= a[i+1];
a[i+1]
= a[i];
a[i]
= tmp;
}
}
}
These aren’t terrible times, but let’s see if
we can do better. Each time we execute one of the inner loops, we use the same
number of threads, so it would seem to be superior to fork the threads once and
reuse the same team of threads for each execution of the inner loops. Not
surprisingly, OpenMP provides directives that allow us to do just this. We can
fork our team of thread count threads before the outer loop with a parallel directive. Then, rather than forking a new
team of threads with each execution of one of the inner loops, we use a for directive, which tells OpenMP to parallelize
the for loop with the existing team of threads. This
modification to the original OpenMP implementation is shown in Program 5.5
The for directive, unlike the parallel for directive, doesn’t fork any threads. It uses whatever threads have
already been forked in the enclosing parallel block.
Program 5.5: Second OpenMP implementation of odd-even sort
# pragma omp parallel num threads(thread count)
\
default(none)
shared(a, n) private(i, tmp, phase)
for
(phase = 0; phase < n; phase++) {
if
(phase % 2 == 0)
# pragma omp for
for
(i = 1; i < n; i += 2) {
if
(a[i- 1] > a[i]) {
tmp
= a[i- 1];
a[i
1] = a[i];
a[i]
= tmp;
}
}
else
#pragma
omp for
for
(i = 1; i < n 1; i += 2) {
if
(a[i] > a[i+1]) {
tmp
= a[i+1];
a[i+1]
= a[i];
a[i]
= tmp;
}
}
}
There is an implicit barrier at the end of the loop. The results of the
code—the final list—will therefore be the same as the results obtained from the
original parallelized code.
Run-times for this second version of odd-even
sort are in the second row of Table 5.2. When we’re using two or more threads,
the version that uses two for direc-tives is at least 17% faster than the version that uses two parallel for directives, so for this system the slight effort involved in
making the change is well worth it.
Related Topics