Caches, Cache Coherence, and False Sharing

CACHES, CACHE COHERENCE, AND FALSE SHARING

Recall that for a number of years now, processors have been able to execute opera-tions much faster than they can access data in main memory, so if a processor must read data from main memory for each operation, it will spend most of its time simply waiting for the data from memory to arrive. Also recall that in order to address this problem, chip designers have added blocks of relatively fast memory to processors. This faster memory is called cache memory.

The design of cache memory takes into consideration the principles of temporal and spatial locality: if a processor accesses main memory location x at time t, then it is likely that at times close to t, it will access main memory locations close to x. Thus, if a processor needs to access main memory location x, rather than transferring only the contents of x to/from main memory, a block of memory containing x is tranferred from/to the processor’s cache. Such a block of memory is called a cache line or cache

block.

We’ve already seen in Section 2.3.4 that the use of cache memory can have a huge impact on shared memory. Let’s recall why. First, consider the following situation. Suppose x is a shared variable with the value 5, and both thread 0 and thread 1 read x from memory into their (separate) caches, because both want to execute the statement

my - y = x;

Here, my y is a private variable defined by both threads. Now suppose thread 0 executes the statement

x++;

Finally, suppose that thread 1 now executes

my_z = x;

where my _z is another private variable.

What’s the value in my_z? Is it 5? Or is it 6? The problem is that there are (at least) three copies of x: the one in main memory, the one in thread 0’s cache, and the one in thread 1’s cache. When thread 0 executed x++, what happened to the values in main memory and thread 1’s cache? This is the cache coherence prob-lem, which we discussed in Chapter 2. We saw there that most systems insist that the caches be made aware that changes have been made to data they are caching. The line in the cache of thread 1 would have been marked invalid when thread 0 executed x++, and before assigning my_z = x, the core running thread 1 would see that it’s value of x was out of date. Thus, the core running thread 0 would have to update the copy of x in main memory (either now or earlier), and the core running thread 1 would get the line with the updated value of x from main memory. For further details, see Chapter 2.

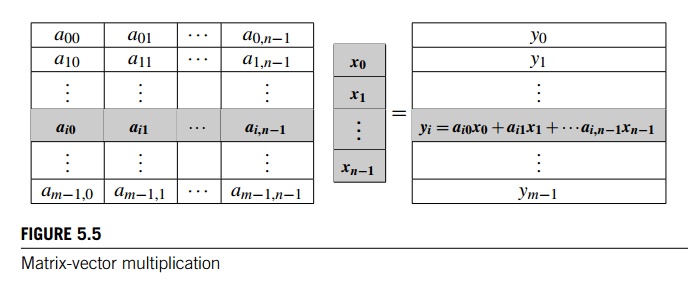
The use of cache coherence can have a dramatic effect on the performance of shared-memory systems. To illustrate this, let’s take a look at matrix-vector multipli-cation. Recall that if A = (a_ij) is an m n matrix and x is a vector with n components, then their product y = Ax is a vector with m components, and its ith component y_i is found by forming the dot product of the ith row of A with x:

yi = a_i0x₀ + a_i1x₁ + ··· + a_i,n−1x_n−1.

See Figure 5.5.

So if we store A as a two-dimensional array and x and y as one-dimensional arrays, we can implement serial matrix-vector multiplication with the following code:

for (i = 0; i < m; i++) { y[i] = 0.0;

for (j = 0; j < n; j++) y[i] += A[i][j] x[j];

}

There are no loop-carried dependences in the outer loop, since A and x are never updated and iteration i only updates y[i]. Thus, we can parallelize this by dividing the iterations in the outer loop among the threads:

          #  pragma omp parallel for     num_threads(thread count)  \

          default(none) private(i, j) shared(A, x, y, m, n)

          for (i = 0; i < m; i++)      {

          y[i] = 0.0;

          for (j = 0; j < n; j++)

          y[i] += A[i][j]* x[j];

          }

If T_serial is the run-time of the serial program and T_parallel is the run-time of the parallel program, recall that the efficiency E of the parallel program is the speedup S divided by the number of threads, t:

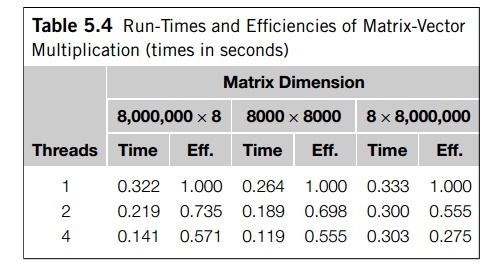
Since S<=t, E<=1. Table 5.4 shows the run-times and efficiencies of our matrix-vector multiplication with different sets of data and differing numbers of threads.

In each case, the total number of floating point additions and multiplications is 64, 000, 000. An analysis that only considers arithmetic operations would predict that a single thread running the code would take the same amount of time for all three inputs. However, it’s clear that this is not the case. The 8, 000, 000 x8 system requires about 22% more time than the 8000x 8000 system, and the 8x 8, 000, 000 system requires about 26% more time than the 8000 x8000 system. Both of these differences are at least partially attributable to cache performance.

Recall that a write-miss occurs when a core tries to update a variable that’s not in cache, and it has to access main memory. A cache profiler (such as Valgrind [49]) shows that when the program is run with the 8, 000, 000x 8 input, it has far more

cache write-misses than either of the other inputs. The bulk of these occur in Line 4. Since the number of elements in the vector y is far greater in this case (8,000,000 vs. 8000 or 8), and each element must be initialized, it’s not surprising that this line slows down the execution of the program with the 8,000,000 x8 input.

Also recall that a read-miss occurs when a core tries to read a variable that’s not in cache, and it has to access main memory. A cache profiler shows that when the program is run with the 8 x8,000,000 input, it has far more cache read-misses than either of the other inputs. These occur in Line 6, and a careful study of this program (see Exercise 5.12) shows that the main source of the differences is due to the reads of x. Once again, this isn’t surprising, since for this input, x has 8,000,000 elements, versus only 8000 or 8 for the other inputs.

It should be noted that there may be other factors that affect the relative perfor-mance of the single-threaded program with differing inputs. For example, we haven’t taken into consideration whether virtual memory (see Section 2.2.4) has affected the performance of the program with the different inputs. How frequently does the CPU need to access the page table in main memory?

Of more interest to us, though, are the differences in efficiency as the num-ber of threads is increased. The two-thread efficiency of the program with the 8 x8,000,000 input is more than 20% less than the efficiency of the program with the 8,000,000 x8 and the 8000 x8000 inputs. The four-thread efficiency of the program with the 8x 8,000,000 input is more than 50% less than the program’s efficiency with the 8,000,000 8 and the 8000x 8000 inputs. Why, then, is the multithreaded performance of the program so much worse with the 8 x8,000,000 input?

In this case, once again, the answer has to do with cache. Let’s take a look at the program when we run it with four threads. With the 8,000,000x 8 input, y has 8,000,000 components, so each thread is assigned 2,000,000 components. With the 8000x 8000 input, each thread is assigned 2000 components of y, and with the 8 x8,000,000 input, each thread is assigned two components. On the system we used, a cache line is 64 bytes. Since the type of y is double, and a double is 8 bytes, a single cache line will store eight doubles.

Cache coherence is enforced at the “cache-line level.” That is, each time any value in a cache line is written, if the line is also stored in another core’s cache, the entire line will be invalidated—not just the value that was written. The system we’re using has two dual-core processors and each processor has its own cache. Suppose for the moment that threads 0 and 1 are assigned to one of the processors and threads 2 and 3 are assigned to the other. Also suppose that for the 8 x 8,000,000 problem all of y is stored in a single cache line. Then every write to some element of y will invalidate the line in the other processor’s cache. For example, each time thread 0 updates y[0] in the statement

y[i] += A[i][j] x[j];

if thread 2 or 3 is executing this code, it will have to reload y. Each thread will update each of its components 8,000,000 times. We see that with this assignment of threads to processors and components of y to cache lines, all the threads will have to reload y many times. This is going to happen in spite of the fact that only one thread accesses any one component of y—for example, only thread 0 accesses y[0].

Each thread will update its assigned components of y a total of 16,000,000 times. It appears that many, if not most, of these updates are forcing the threads to access main memory. This is called false sharing. Suppose two threads with separate caches access different variables that belong to the same cache line. Further suppose at least one of the threads updates its variable. Even though neither thread has written to a shared variable, the cache controller invalidates the entire cache line and forces the other threads to get the values of the variables from main memory. The threads aren’t sharing anything (except a cache line), but the behavior of the threads with respect to memory access is the same as if they were sharing a variable. Hence the name false

sharing.

Why is false sharing not a problem with the other inputs? Let’s look at what happens with the 8000 8000 input. Suppose thread 2 is assigned to one of the pro-cessors and thread 3 is assigned to another. (We don’t actually know which threads are assigned to which processors, but it turns out—see Exercise 5.13—that it doesn’t matter.) Thread 2 is responsible for computing

y[4000], y[4001], . . . , y[5999],

and thread 3 is responsible for computing

y[6000], y[6001], . . . , y[7999]

If a cache line contains eight consecutive doubles, the only possibility for false shar-ing is on the interface between their assigned elements. If, for example, a single cache line contains

y[5996], y[5997], y[5998], y[5999], y[6000], y[6001], y[6002], y[6003],

then it’s conceivable that there might be false sharing of this cache line. However, thread 2 will access

y[5996], y[5997], y[5998], y[5999]

at the end of its iterations of the for i loop, while thread 3 will access

y[6000], y[6001], y[6002], y[6003]

at the beginning of its iterations. So it’s very likely that when thread 2 accesses, say, y[5996], thread 3 will be long done with all four of

y[6000], y[6001], y[6002], y[6003].

Similarly, when thread 3 accesses, say, y[6003], it’s very likely that thread 2 won’t be anywhere near starting to access