The Target Concentration Approach to Designing a Rational Dosage Regimen

THE TARGET CONCENTRATION APPROACH TO DESIGNING A RATIONAL DOSAGE REGIMEN

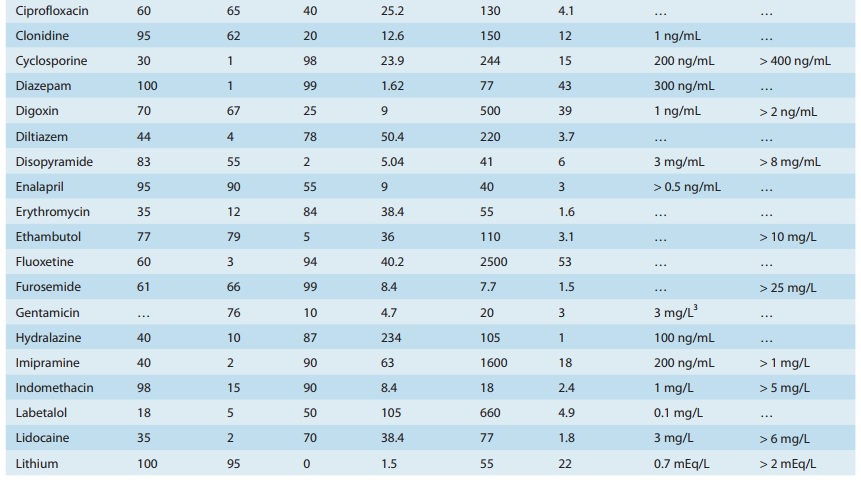
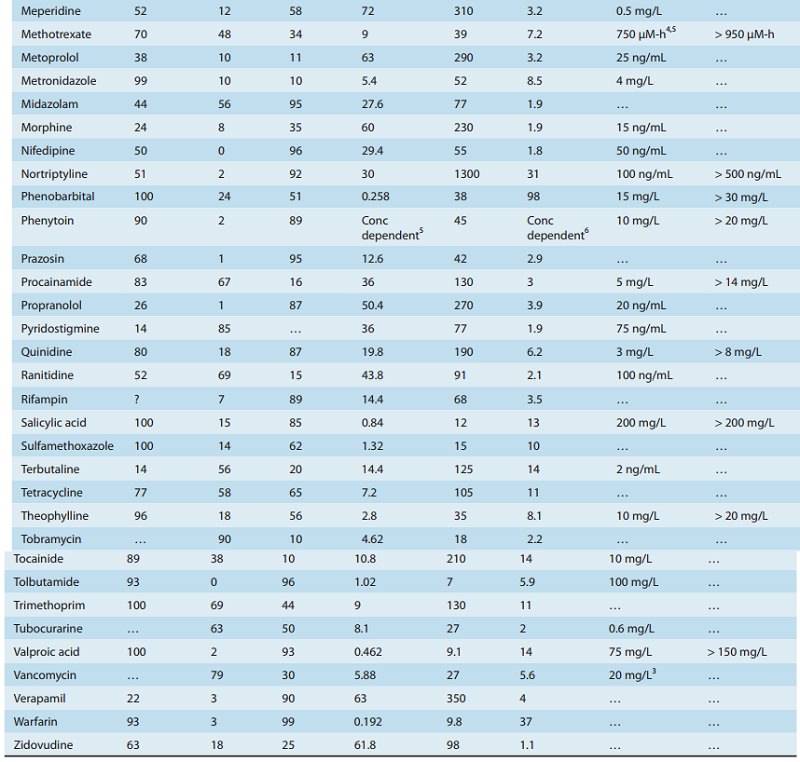
A rational dosage regimen is based on the assumption that there is a target concentration that will produce the desired therapeutic effect. By considering the pharmacokinetic factors that determine the dose-concentration relationship, it is possible to individualize the dose regimen to achieve the target concentration. The effective concentration ranges shown in Table 3–1 are a guide to the con-centrations measured when patients are being effectively treated. The initial target concentration should usually be chosen from the lower end of this range. In some cases, the target concentration will also depend on the specific therapeutic objective—eg, the control of atrial fibrillation by digoxin often requires a target concentration of 2 ng/mL, while heart failure is usually adequately managed with a target concentration of 1 ng/mL.

Maintenance Dose

In most clinical situations, drugs are administered in such a way as to maintain a steady state of drug in the body, ie, just enough drug is given in each dose to replace the drug eliminated since the preceding dose. Thus, calculation of the appropriate maintenance dose is a primary goal. Clearance is the most important pharma-cokinetic term to be considered in defining a rational steady-state drug dosage regimen. At steady state, the dosing rate (“rate in”) must equal the rate of elimination (“rate out”). Substitution of the target concentration (TC) for concentration (C) in equation (4) predicts the maintenance dosing rate:

Thus, if the desired target concentration is known, the clearance in that patient will determine the dosing rate. If the drug is given by a route that has a bioavailability less than 100%, then the dosing rate predicted by equation (9) must be modified. For oral dosing:

If intermittent doses are given, the maintenance dose is calcu-lated from:

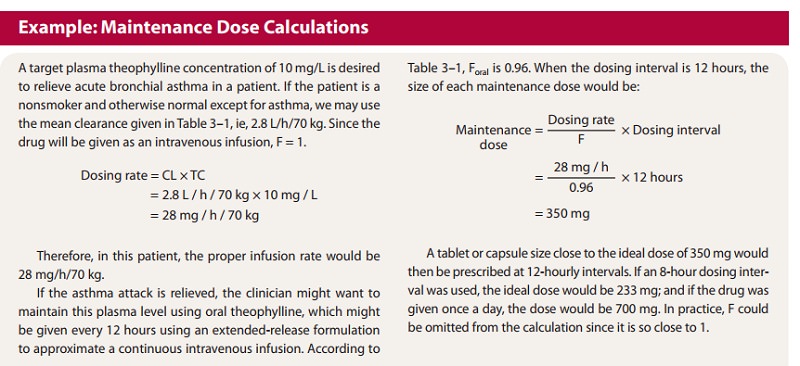
(See Box: Example: Maintenance Dose Calculations.)

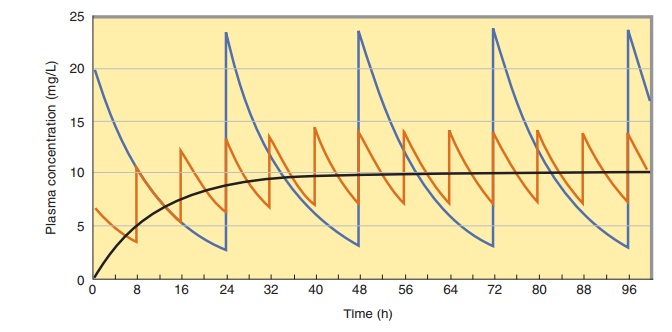
Note that the steady-state concentration achieved by con-tinuous infusion or the average concentration following inter-mittent dosing depends only on clearance. The volume of distribution and the half-life need not be known in order to determine the average plasma concentration expected from a given dosing rate or to predict the dosing rate for a desired tar-get concentration. Figure 3–6 shows that at different dosing intervals, the concentration-time curves will have different maximum and minimum values even though the average level will always be 10 mg/L.

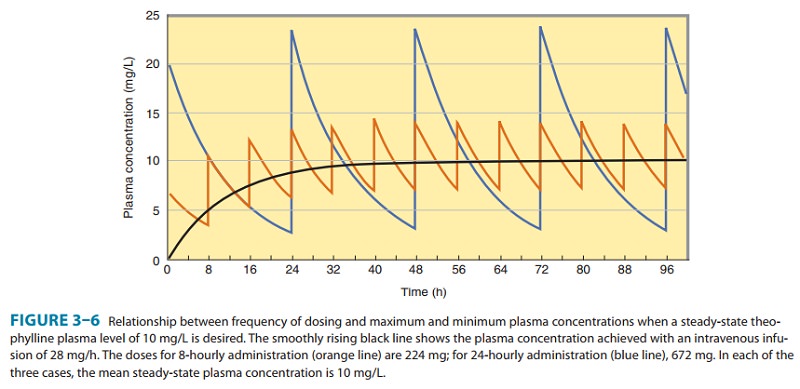
Estimates of dosing rate and average steady-state concentra-tions, which may be calculated using clearance, are independent of any specific pharmacokinetic model. In contrast, the determi-nation of maximum and minimum steady-state concentrations requires further assumptions about the pharmacokinetic model. The accumulation factor (equation [7]) assumes that the drug fol-lows a one-compartment body model (Figure 3–2B), and the peak concentration prediction assumes that the absorption rate is much faster than the elimination rate. For the calculation of estimated maximum and minimum concentrations in a clinical situation, these assumptions are usually reasonable.

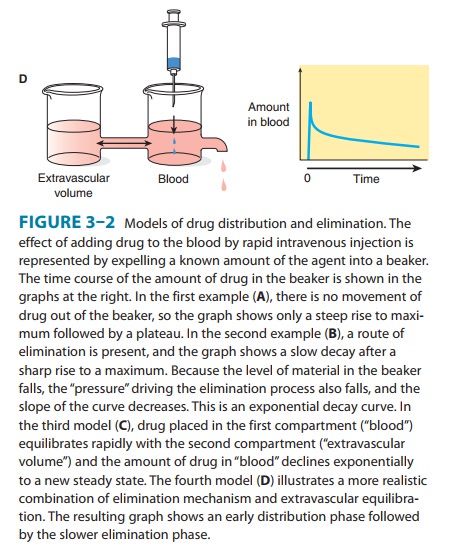
Loading Dose

When the time to reach steady state is appreciable, as it is for drugs with long half-lives, it may be desirable to administer a loading dose that promptly raises the concentration of drug in plasma to the target concentration. In theory, only the amount of the load-ing dose need be computed—not the rate of its administration— and, to a first approximation, this is so. The volume of distribution is the proportionality factor that relates the total amount of drug in the body to the concentration; if a loading dose is to achieve the target concentration, then from equation (1):

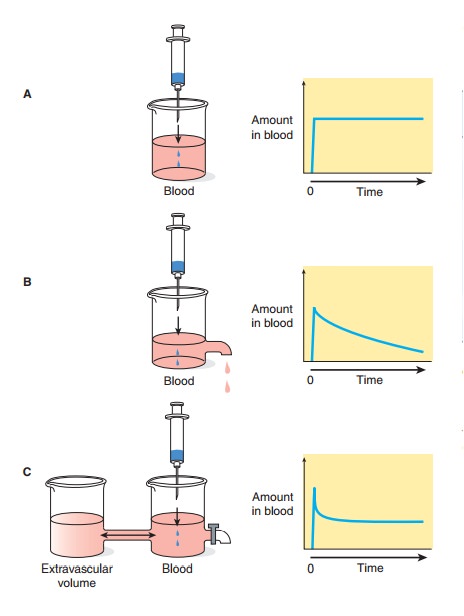
For the theophylline example given in the Box, Example: Maintenance Dose Calculations, the loading dose would be 350 mg (35 L × 10 mg/L) for a 70-kg person. For most drugs, the loading dose can be given as a single dose by the chosen route of administration. Up to this point, we have ignored the fact that some drugs follow more complex multicompartment pharmacokinetics, eg, the distribution process illustrated by the two-compartment model in Figure 3–2. This is justified in the great majority of cases. However, in some cases the distribution phase may not be ignored, particularly in connection with the calculation of load-ing doses. If the rate of absorption is rapid relative to distribution (this is always true for rapid intravenous administration), the concentration of drug in plasma that results from an appropriate loading dose—calculated using the apparent volume of distribu-tion—can initially be considerably higher than desired. Severe toxicity may occur, albeit transiently. This may be particularly important, eg, in the administration of antiarrhythmic drugs such as lidocaine, where an almost immediate toxic response may occur. Thus, while the estimation of the amount of a loading dose may be quite correct, the rate of administration can sometimes be crucial in preventing excessive drug concentrations, and slow administration of an intravenous drug (over minutes rather than seconds) is almost always prudent practice.

When intermittent doses are given, the loading dose calculated from equation (12) will only reach the average steady-state concentration and will not match the peak steady-state concentration (Figure 3–6). To match the peak steady-state con-centration, the loading dose can be calculated from equation (13):