Statement, Proof, Construction, Illustration, Solved Example Problems - Thales Theorem and Angle Bisector Theorem | 10th Mathematics : UNIT 4 : Geometry
Chapter: 10th Mathematics : UNIT 4 : Geometry
Thales Theorem and Angle Bisector Theorem
Thales Theorem and Angle Bisector Theorem
Introduction
Thales, (640 - 540 BC (BCE)) the most famous Greek mathematician
and philosopher lived around seventh century BC (BCE). He possessed knowledge
to the extent that he became the first of seven sages of Greece. Thales was the
first man to announce that any idea that emerged should be tested
scientifically and only then it can be accepted. In this aspect, he did great
investigations in mathematics and astronomy and discovered many concepts. He
was credited for providing first proof in mathematics, which today is called by
the name “Basic Proportionality Theorem”. It is also called “Thales Theorem”
named after its discoverer.

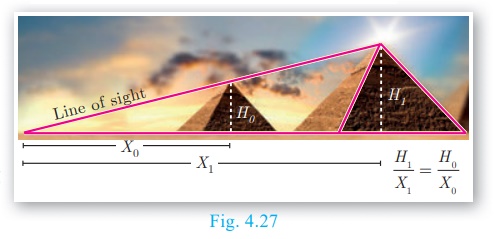
The discovery of the Thales theorem itself is a very interesting
story. When Thales travelled to Egypt, he was challenged by Egyptians to
determine the height of one of several magnificent pyramids that they had
constructed. Thales accepted the challenge and used similarity of triangles to
determine the same successfully, another triumphant application of Geometry.
Since X0, X1 and H0 are
known, we can determine the height H1 of the pyramid.
To understand the basic proportionality theorem or Thales theorem, let us do the following
activity.
Theorem 1:
Basic Proportionality Theorem (BPT) or Thales theorem
Statement
A straight line drawn parallel to a side of triangle intersecting
the other two sides, divides the sides in the same ratio.
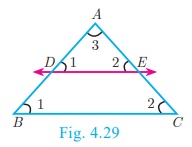
Proof
Given: In ΔABC , D is a point on AB and E is a point on AC.
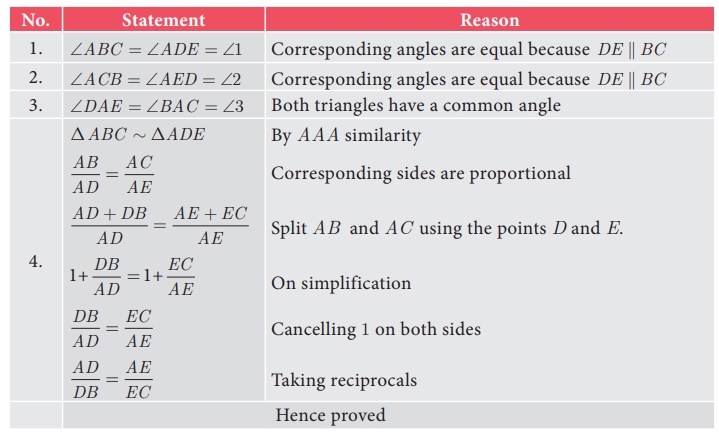
To prove:
AD/DB =
AE/EC
Construction:
Draw a line DE || BC
Corollary
If in ΔABC , a straight line DE parallel to BC,
intersects AB at D and AC at E, then

Proof
In ΔABC, DE || BC.
therefore,  => AD/DB = AE/EC (by Basic
Proportionality Theorem)
=> AD/DB = AE/EC (by Basic
Proportionality Theorem)

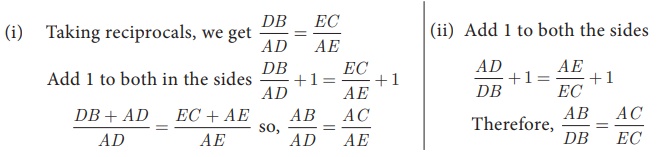
Is the converse of Basic Proportionality Theorem also true? To examine let us do the following illustration.
Illustration
Draw an angle XAY on your notebook as shown in Fig.4.31 and
on ray AX, mark points B1 , B2 , B
3 , B4 and B such that AB1
= B1B2 = B2 B3
= B 3 B4 = B 4 B =
1 cm.
Similarly on ray AY, mark points C1, C2
, C3 ,C4 and C, such that AC1=C1C2
= C2C3 = C3C4
= C4C = 2 cm, Join B1 C1
and BC
Observe that 
Similarly joining B2C2, B3C3
and B4C4 you see that

From this we observe that if a line divides two sides of a
triangle in the same ratio, then the line is parallel to the third side.
Therefore, we obtain the following theorem called converse of the Thales theorem.
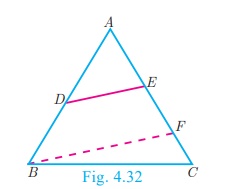
Theorem 2:
Converse of Basic Proportionality Theorem
Statement
If a straight line divides any two sides of a triangle in the same
ratio, then the line must be parallel to the third side.
Proof
Given : In ABC, 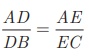
To prove : DE || BC
Construction Draw BF || DE

Theorem 3:
Angle Bisector Theorem
Statement
The internal bisector of an angle of a triangle divides the
opposite side internally in the ratio of the corresponding sides containing the
angle.
Proof
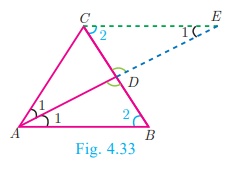
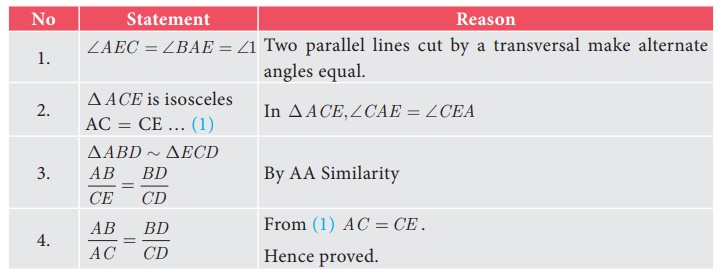
Given : In ΔABC, AD is the internal
bisector
To prove : 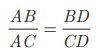
Construction : Draw a line through C parallel to AB. Extend AD to
meet line through C at E
Theorem 4:
Converse of Angle Bisector Theorem
Statement
If a straight line through one vertex of a triangle divides the
opposite side internally in the ratio of the other two sides, then the line
bisects the angle internally at the vertex.
Proof
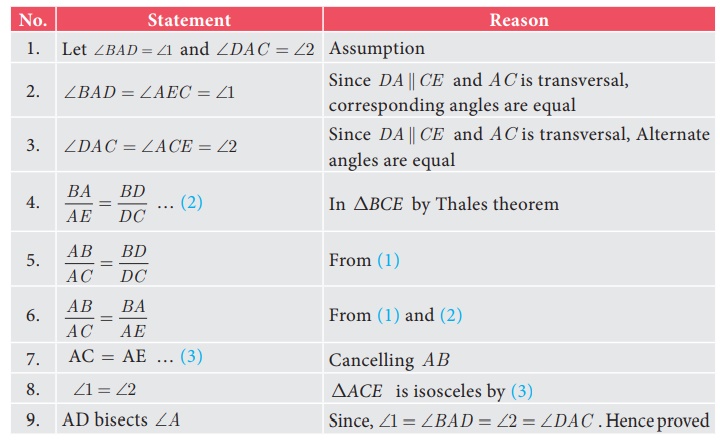
Given : ABC is a triangle. AD divides BC in the ratio of the
sides containing the angles ∠A to meet BC at D.
That is 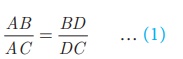
To prove : AD bisects ∠A i.e. ∠1 = ∠2
Construction : Draw CE || DA . Extend BA to meet at E.

Example 4.12
In ΔABC , if DE || BC , AD = x, DB = x −
2, and EC = x −1 then find the lengths of
the sides AB and AC.
Solution
In ΔABC we have DE || BC .
By Thales theorem, we have
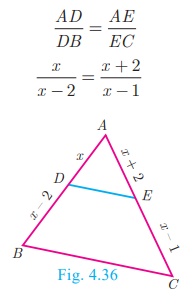
x/ x-2 = (x + 2)/(x - 1) gives x
(x − 1) = (x − 2)(x + 2)
Hence, x 2 − x = x2 – 4 so, x = 4
When x = 4 , AD = 4 , DB = x − 2 = 2 ,
AE = x + 2 = 6 , EC = x – 1 =3
Hence, AB = AD + DB = 4 + 2 = 6 , AC =
AE + EC = 6 + 3 = 9 .
Therefore, AB = 6, AC = 9.
Example 4.13
D and E are respectively the points on the sides AB and AC of a ΔABC such that AB=5.6
cm, AD=1.4 cm, AC=7.2 cm and AE = 1.8 cm, show that DE || BC.
Solution
We have AB = 5.6 cm, AD =1.4 cm, AC 7.2
cm and AE = 1.8 cm.
BD = AB − AD = 5.6–1.4 = 4.2 cm
and EC = AC –AE = 7.2–1.8 = 5.4 cm.
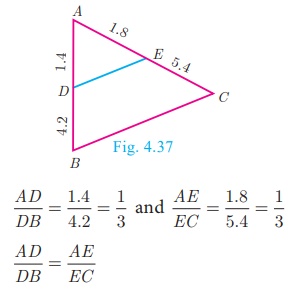
Therefore, by converse of Basic Proportionality Theorem, we have DE is
parallel to BC.
Hence proved.
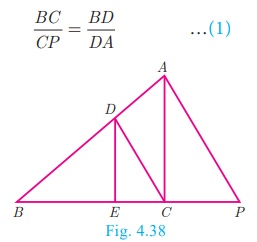
Example 4.14
In the Fig.4.38, DE || AC and DC || AP . Prove that  .
.
Solution
Solution In ΔBPA, we have DC || AP . By Basic Proportionality
Theorem,
we have
In ΔBCA, we have DE || AC . By Basic Proportionality
Theorem, we have
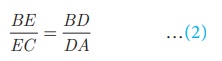
From (1) and (2) we get, BE/EC = BC/CP =>  . Hence proved.
. Hence proved.
Example 4.15
In the Fig.4.39, AD is the bisector of ∠A . If BD = 4 cm, DC = 3 cm and AB =
6 cm, find AC.
Solution
In ΔABC , AD is the bisector of ∠A
Therefore by Angle Bisector Theorem
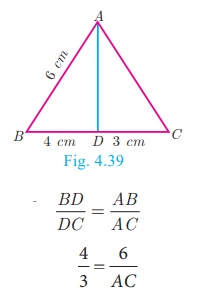
4/3 = 6/ AC
gives 4AC = 8 . Hence, AC = 9/2 =4.5 cm
Example 4.16
In the Fig. 4.40, AD is the bisector of ∠BAC , if AB = 10 cm, AC = 14 cm and BC = 6 cm. Find BD
and DC.
Solution
Let BD = x cm, then DC = (6–x)cm
AD is the bisector of ∠A
Therefore by Angle Bisector Theorem
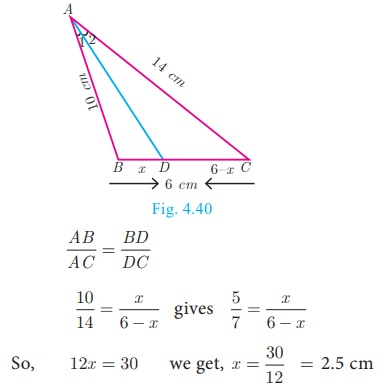
Therefore, BD = 2.5 cm, DC = 6 −
x = 6 − 2.5 = 3.5 cm
Related Topics