Circles and Tangents

Circles and Tangents

In our day-to-day real life situations, we have seen two lines intersect at a point or do not intersect in a plane. For example, two parallel lines in a railway track, do not intersect. Whereas, grills in a window intersect.

Similarly what happens when a curve and a line is given in a plane? The curve may be parabola, circle or any general curve.

Similarly, what happens when we consider intersection of a line and a circle?

We may get three situations as given in the following diagram

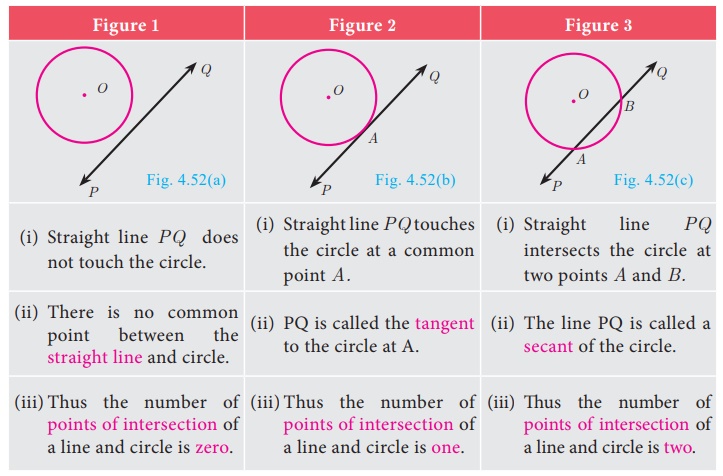
Note

The line segment AB inscribed in the circle in Fig.4.52(c) is called chord of the circle. Thus a chord is a sub-section of a secant.

Definition

If a line touches the given circle at only one point, then it is called tangent to the circle.

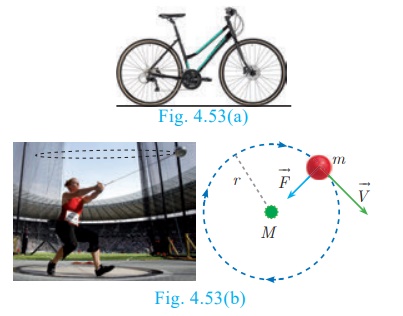
Real life examples of tangents to circles

(i) When a cycle moves along a road, then the road becomes the tangent at each point when the wheels rolls on it.

(ii) When a stone is tied at one end of a string and is rotated from the other end, then the stone will describe a circle. If we suddenly stop the motion, the stone will go in a direction tangential to the circular motion.

Some results on circles and tangents

1. A tangent at any point on a circle and the radius through the point are perpendicular to each other.

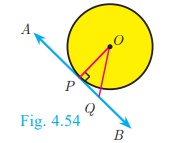
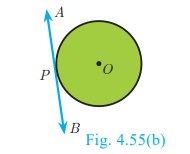
2. (a) No tangent can be drawn from an interior point of the circle.

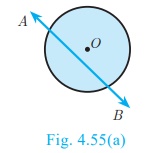
(b) Only one tangent can be drawn at any point on a circle.

(c) Two tangents can be drawn from any exterior point of a circle.

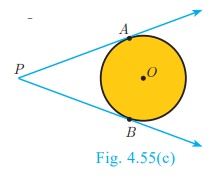
3. The lengths of the two tangents drawn from an exterior point to a circle are equal,

Proof : By 1. OA ┴ PA,OB ┴ PB . Also OA=OB= radius,

OP is common side. ∠AOP = ∠BOP

Therefore, ΔOAP ≅ ΔOBP . Hence PA = PB

4. If two circles touch externally the distance between their centers is equal to the sum of their radii, that is OP = r₁ + r₂

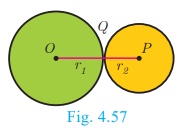
Proof :

Let two circles with centers at O and P touch other at Q.

Let OQ = r₁  and PQ = r₂  and let r₁ > r₂ .

The distance between their centers OP = d . It is clear from the Fig. 4.57 that when the circles touch externally OP = d = OQ + PQ = r₁ + r₂ .

5. If two circles touch internally, the distance between their centers is equal to the difference of their radii, that is OP = r₁ −r₂ .

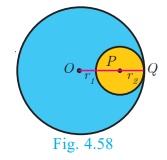
Proof : Let two circles with centers at O and P touch each other at Q. Let OQ = r₁  and PQ = r₂  and let r₁ > r₂ .

The distance between their centers OP = d . It is clear from the Fig. 4.58 that when the circles touch internally, OP = d = OQ – PQ

OP = r₁ −r₂ .

6. The two direct common tangents drawn to the circles are equal in length, that is AB = CD.

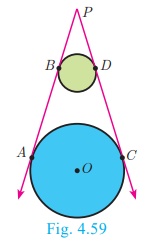
Proof :

The lengths of tangents drawn from P to the two circles are equal.

Therefore, PA = PC and PB = PD.

gives PA − PB = PC – PD

AB = CD

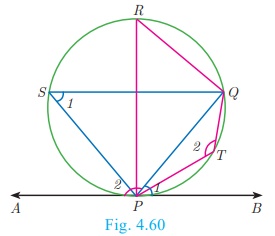
Alternate segment

In the Fig. 4.60, the chord PQ divides the circle into two segments. The tangent AB is drawn such that it touches the circle at P.

The angle in the alternate segment for ∠QPB (∠1) is ∠QSP (∠1) and that for ∠QPA (∠2) is ∠PTQ (∠2) .

Theorem 6 : Alternate Segment theorem

Statement

If a line touches a circle and from the point of contact a chord is drawn, the angles between the tangent and the chord are respectively equal to the angles in the corresponding alternate segments.

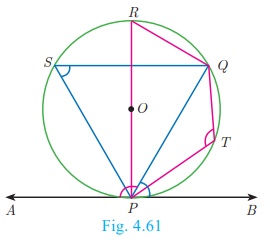
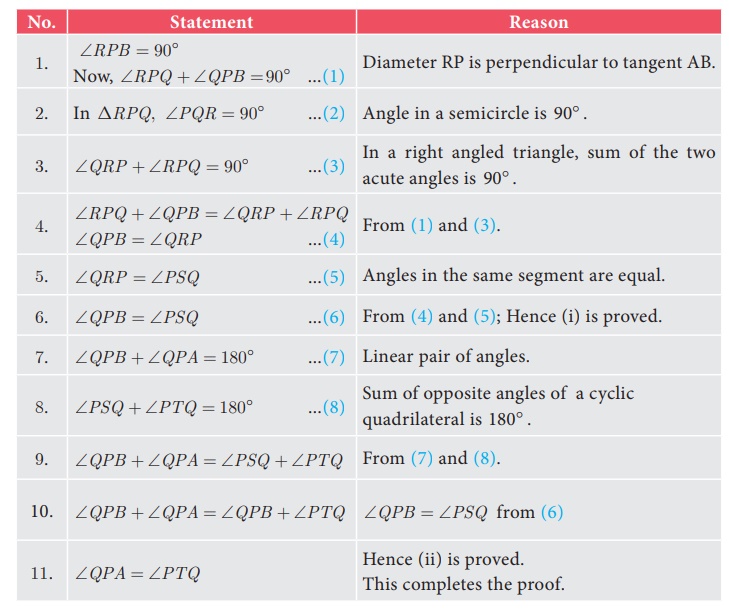
Proof

Given : A circle with centre at O, tangent AB touches the circle at P and PQ is a chord. S and T are two points on the circle in the opposite sides of chord PQ.

To prove : (i) ∠QPB = ∠PSQ and (ii) ∠QPA = ∠PTQ

Construction: Draw the diameter POR. Draw QR, QS and PS.

Example 4.24

Find the length of the tangent drawn from a point whose distance from the centre of a circle is 5 cm and radius of the circle is 3 cm.

Solution

Given OP = 5 cm, radius r = 3 cm

To find the length of tangent PT.

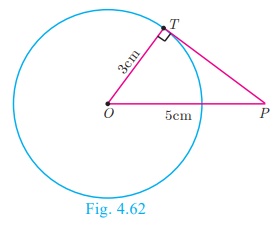
In right angled ΔOTP,

OP²  = OT² + PT²  (by Pythagoras theorem)

5²  = 3² + PT ²   gives PT ²  = 25 − 9 = 16

Length of the tangent PT = 4 cm

Example 4.25

PQ is a chord of length 8 cm to a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length of the tangent TP.

Solution

Let TR = y . Since, OT is perpendicular bisector of PQ.

PR = QR = 4 cm

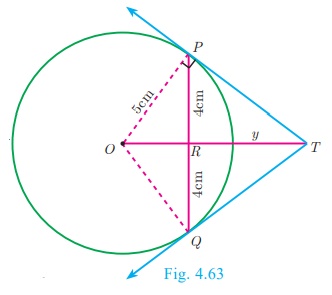
In ΔORP, OP ²  = OR² + PR²

OR ²  = OP² − PR²

OR²  = 5² − 4² = 25 −16 = 9 ⇒ OR = 3 cm

OT = OR+RT = 3+y           ... (1)

In ΔPRT , TP²  = TR² + PR²           … (2)

and ΔOPT we have, OT²  = TP² +OP²

OT²  = (TR²  + PR² ) +OP²  (substitute for TP² from (2))

(3 + y )² = y² + 4 ² + 5²  (substitute for OT from (1))

9 + 6y + y² = y ² + 16 + 25 Therefore y = TR = 16/3

6y = 41 − 9 we get y = 16/3

From (2), TP²  = TR² + PR²

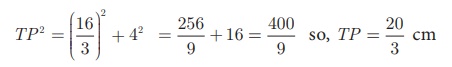
Example 4.26

In Fig.4.64, O is the centre of a circle. PQ is a chord and the tangent PR at P makes an angle of 50° with PQ. Find ∠POQ .

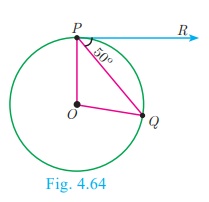
Solution

∠OPQ = 90° − 50° = 40° (angle between the radius and tangent is 90° )

OP = OQ (Radii of a circle are equal)

∠OPQ = ∠OQP = 40° (ΔOPQ is isosceles)  

∠POQ = 180° − ∠OPQ − ∠OQP

∠POQ = 180° − 40° − 40° = 100°

Example 4.27

In Fig.4.65, ΔABC is circumscribing a circle. Find the length of BC.

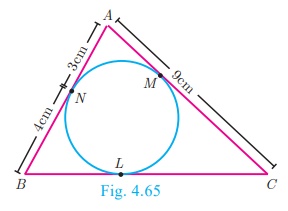
Solution

AN = AM = 3 cm (Tangents drawn from same external point are equal)

BN = BL = 4 cm

CL = CM = AC – AM = 9 – 3 = 6 cm

Gives BC = BL + CL = 4 + 6 = 10 cm

Example 4.28

If radii of two concentric circles are 4 cm and 5 cm then find the length of the chord of one circle which is a tangent to the other circle.

Solution

OA = 4 cm, OB = 5 cm; also OA ┴ BC .

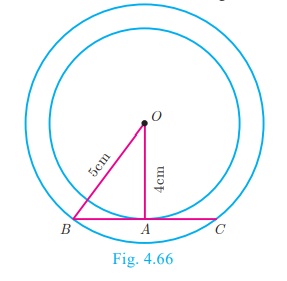
OB ²  = OA² + AB²

5²  = 4² + AB² gives AB²  = 9

Therefore AB = 3 cm

BC = 2AB hence BC = 2 ×3 = 6 cm

Construction

Construction of tangents to a circle

Now let us discuss how to draw

(i) a tangent to a circle using its centre

(ii) a tangent to a circle using alternate segment theorem

(iii) pair of tangents from an external point

Construction of a tangent to a circle (Using the centre)

Example 4.29

Draw a circle of radius 3 cm. Take a point P on this circle and draw a tangent at P.

Solution 

Given, radius r = 3 cm

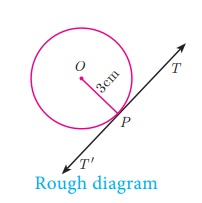
Construction

Step 1: Draw a circle with centre at O of radius 3 cm.

Step 2: Take a point P on the circle. Join OP.

Step 3: Draw  perpendicular  line TT’  to  OP which  passes through P.

Step 4: TT ^‘ is the required tangent.

Construct of a tangent to a circle (Using alternate segment theorem)

Example 4.30

Draw a circle of radius 4 cm. At a point L on it draw a tangent to the circle using the alternate segment.

Solution

Given, radius=4 cm

Construction

Step 1 : With O as the centre, draw a circle of radius 4 cm.

Step 2: Take a point L on the circle. Through L draw any chord LM.

Step 3: Take a point M distinct from L and N on the circle, so that L, M and N are  in anti-clockwise direction. Join  LN and NM.

Step 4: Through L draw a tangent TT ’ such that ∠TLM = ∠MNL.

Step 5: TT ‘ is the required tangent.

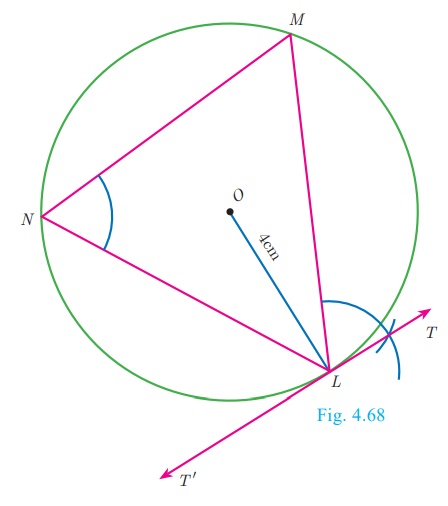
Construction of pair of tangents to a circle from an external point P.

Example 4.31

Draw a circle of diameter 6 cm from a point P, which is 8 cm away from its centre. Draw the two tangents PA and PB to the circle and measure their lengths.

Solution

Given, diameter (d) = 6 cm, we find radius (r) = 6/2 = 3 cm

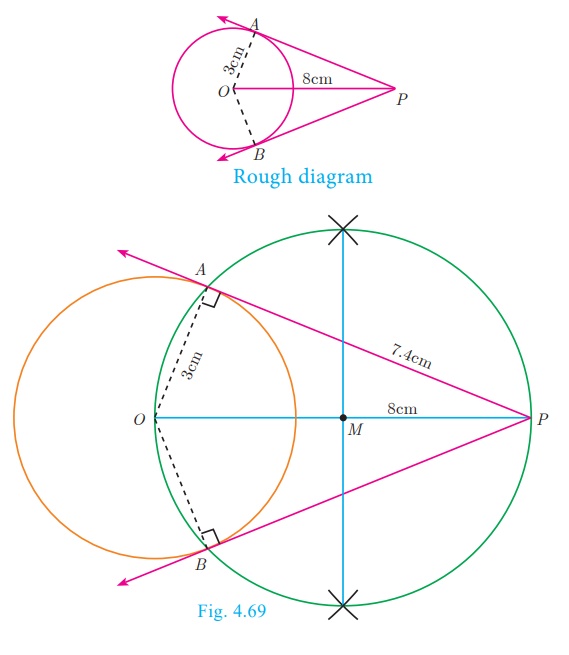
Construction

Step 1: With centre at O, draw a circle of radius 3 cm.

Step 2: Draw a line OP of length 8 cm.

Step 3: Draw a perpendicular bisector of OP, which cuts OP at M.

Step 4: With M as centre and MO as radius, draw a circle which cuts previous circle at A and B.

Step5: Join AP and BP. AP and BP are the required tangents. Thus length of the tangents are PA = PB = 7.4 cm.

Verification : In the right angle triangle OAP , PA²  = OP² −OA²  = 64 – 9 = 55

PA = √55 = 7 4. cm (approximately) .