Exercise 4.4: Concurrency Theorems

Exercise 4.4

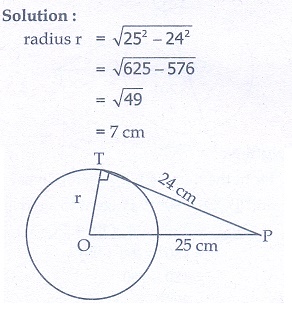
1. The length of the tangent to a circle from a point P, which is 25 cm away from the centre is 24 cm. What is the radius of the circle?

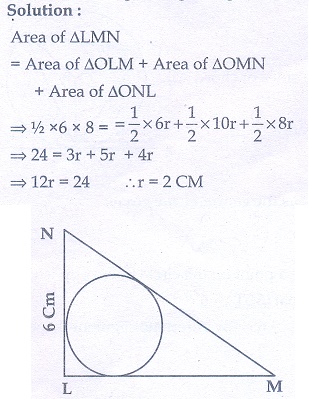
2. ΔLMN is a right angled triangle with ∠L = 90° . A circle is inscribed in it. The lengths of the sides containing the right angle are 6 cm and 8 cm. Find the radius of the circle.

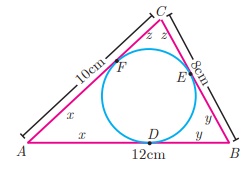
3. A circle is inscribed in DABC having sides 8 cm, 10 cm and 12 cm as shown in figure,

Find AD, BE and CF

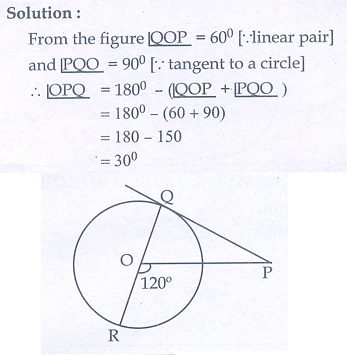
4. PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120° . Find ∠OPQ .

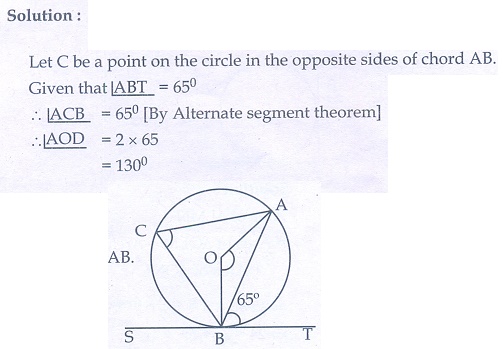
5. A tangent ST to a circle touches it at B. AB is a chord such that ∠ABT = 65° . Find ∠AOB , where “O” is the centre of the circle.

6. In figure, O is the centre of the circle with radius 5 cm. T is a point such that OT = 13 cm and OT intersects the circle E, if AB is the tangent to the circle at E, find the lenght of AB.

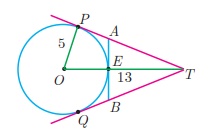
7. In two concentric circles, a chord of length 16 cm of larger circle becomes a tangent to the smaller circle whose radius is 6 cm. Find the radius of the larger circle.

8. Two circles with centres O and O’ of radii 3 cm and 4 cm, respectively intersect at two points P and Q, such that OP and O’P are tangents to the two circles. Find the length of the common chord PQ.

9. Show that the angle bisectors of a triangle are concurrent.

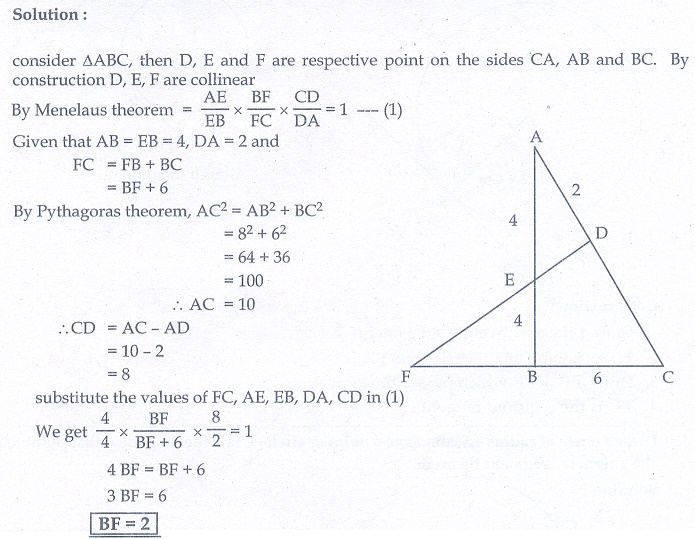
10. In ΔABC , with ∠B = 90° , BC = 6 cm and AB = 8 cm, D is a point on AC such that AD = 2 cm and E is the midpoint of AB. Join D to E and extend it to meet at F. Find BF

11. An artist has created a triangular stained glass window and has one strip of small length left before completing the window. She needs to figure out the length of left out portion based on the lengths of the other sides as shown in the figure.

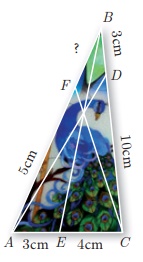
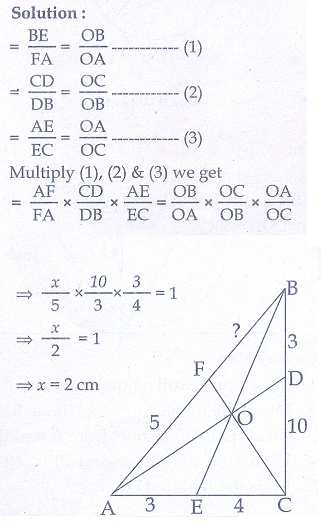
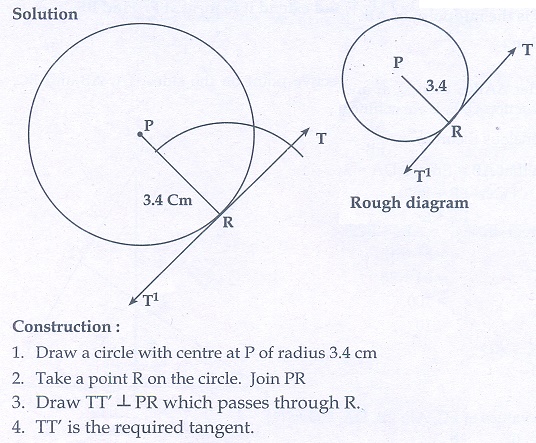
12. Draw a tangent at any point R on the circle of radius 3.4 cm and centre at P ?

13. Draw a circle of radius 4.5 cm. Take a point on the circle. Draw the tangent at that point using the alternate segment theorem.

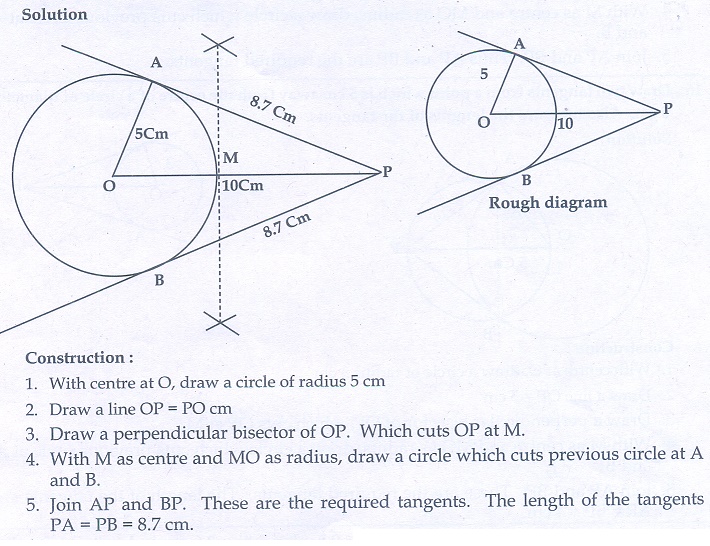
14. Draw the two tangents from a point which is 10 cm away from the centre of a circle of radius 5 cm. Also, measure the lengths of the tangents.

15. Take a point which is 11 cm away from the centre of a circle of radius 4 cm and draw the two tangents to the circle from that point.

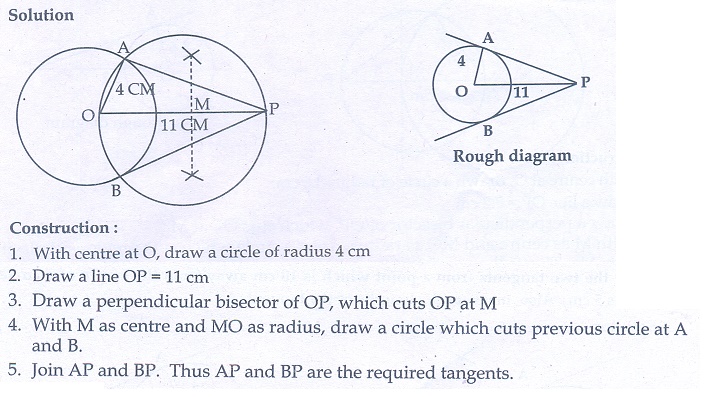
16. Draw the two tangents from a point which is 5 cm away from the centre of a circle of diameter 6 cm. Also, measure  the lengths of the tangents.

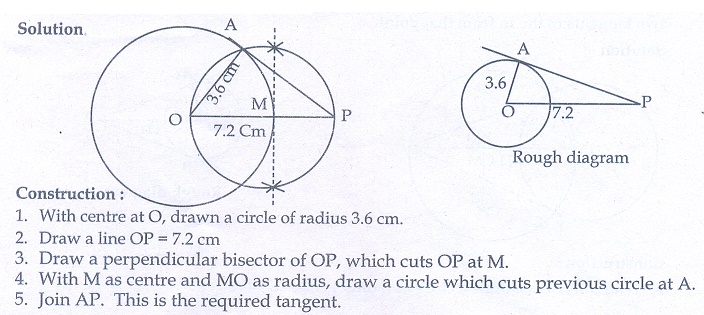
17. Draw a tangent to the circle from the point P having radius 3.6 cm, and centre at O. Point P is at a distance 7.2 cm from the centre.

 Answers:

1. 7 cm 

2. 2 cm 

3. 7 cm, 5 cm, 3 cm

4. 30°

5. 130°

6. 20/3 cm

7. 10 cm

8. 4.8 cm

10. 2 cm

11. 2 cm

14. 8.7 cm

16. 4 cm