Construction of tangents to a circle

Construction

Construction of tangents to a circle

Now let us discuss how to draw

(i) a tangent to a circle using its centre

(ii) a tangent to a circle using alternate segment theorem

(iii) pair of tangents from an external point

Construction of a tangent to a circle (Using the centre)

Example 4.29

Draw a circle of radius 3 cm. Take a point P on this circle and draw a tangent at P.

Solution 

Given, radius r = 3 cm

Construction

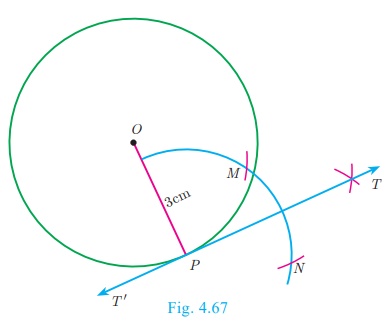
Step 1: Draw a circle with centre at O of radius 3 cm.

Step 2: Take a point P on the circle. Join OP.

Step 3: Draw  perpendicular  line TT’  to  OP which  passes through P.

Step 4: TT ‘ is the required tangent.

Construct of a tangent to a circle (Using alternate segment theorem)

Example 4.30

Draw a circle of radius 4 cm. At a point L on it draw a tangent to the circle using the alternate segment.

Solution

Given, radius=4 cm

Construction

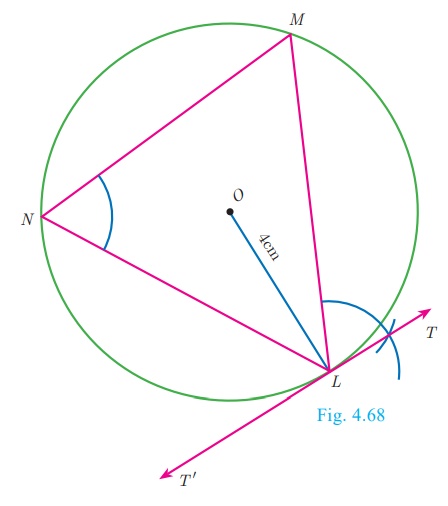
Step 1 : With O as the centre, draw a circle of radius 4 cm.

Step 2: Take a point L on the circle. Through L draw any chord LM.

Step 3: Take a point M distinct from L and N on the circle, so that L, M and N are  in anti-clockwise direction. Join  LN and NM.

Step 4: Through L draw a tangent TT ’ such that ∠TLM = ∠MNL.

Step 5: TT ‘ is the required tangent.

Construction of pair of tangents to a circle from an external point P.

Example 4.31

Draw a circle of diameter 6 cm from a point P, which is 8 cm away from its centre. Draw the two tangents PA and PB to the circle and measure their lengths.

Solution

Given, diameter (d) = 6 cm, we find radius (r) = 6/2 = 3 cm

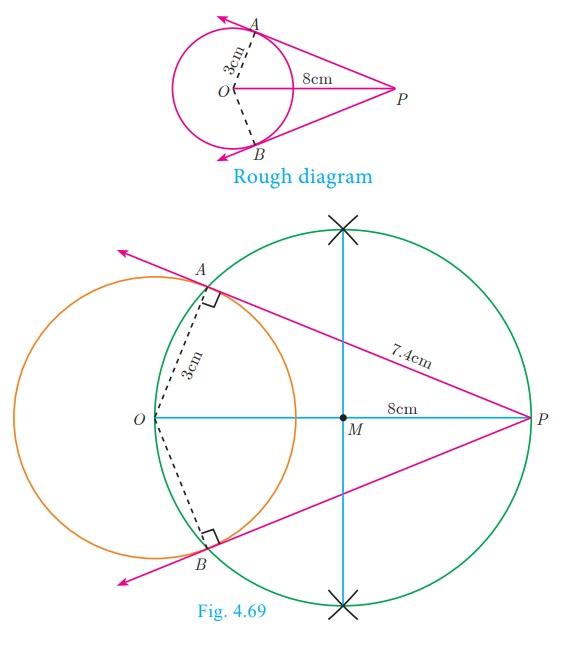
Construction

Step 1: With centre at O, draw a circle of radius 3 cm.

Step 2: Draw a line OP of length 8 cm.

Step 3: Draw a perpendicular bisector of OP, which cuts OP at M.

Step 4: With M as centre and MO as radius, draw a circle which cuts previous circle at A and B.

Step5: Join AP and BP. AP and BP are the required tangents. Thus length of the tangents are PA = PB = 7.4 cm.

Verification : In the right angle triangle OAP , PA2  = OP2 −OA2  = 64 – 9 = 55

PA = √55 = 7 4. cm (approximately) .