Concurrency Theorems

Concurrency Theorems

Definition

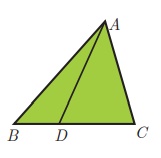
A cevian is a line segment that extends from one vertex of a triangle to the opposite side. In the diagram, AD is a cevian, from A.

Special cevians

(i) A median is a cevian that divides the opposite side into two congruent(equal) lengths.

(ii) An altitude is a cevian that is perpendicular to the opposite side.

(ii) An angle bisector is a cevian that bisects the corresponding angle.

Ceva’s Theorem (without proof)

Statement

Let ABC be a triangle and let D,E,F be points on lines BC, CA,  AB respectively.  Then the cevians AD,  BE, CF are concurrent if and only if  = 1 where the lengths are directed. This also works for the reciprocal of each of the ratios B as the reciprocal of 1 is 1.

Note

The cevians do not necessarily lie within the triangle, although they do in the diagram.

Menelaus Theorem (without proof) 

Statement

A necessary and sufficient condition for points P, Q, R on the respective sides BC, CA, AB (or their extension) of a triangle ABC to be collinear is that  where all segments in the formula are directed segments.

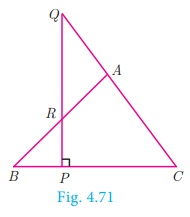
Note

·           Menelaus theorem can also be given as BP × CQ ×AR = −PC × QA×RB.

·           If BP is replaced by PB (or) CQ by QC (or) AR by RA, or if any one of the six directed line segments BP, PC, CQ, QA, AR, RB is interchanged, then the product will be 1.

Example 4.32 Show that in a triangle, the medians are concurrent.

Solution

Medians are line segments joining each vertex to the midpoint of the corresponding opposite sides.

Thus medians are the cevians where D, E, F are midpoints of BC, CA and AB respectively.

Since D is a midpoint of BC, BD = DC so  BD/DC =1            ………..(1)

Since, E is a midpoint of CA, CE = EA so   CE/EA =1            ………..(1)

Since, F is a midpoint of AB, AF = FB so    AF/FB =1            ………..(1)

Thus, multiplying (1), (2) and (3) we get, 

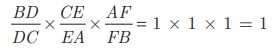
And so, Ceva’s theorem is satisfied.

Hence the Medians are concurrent.

Example 4.33

In Fig.4.73, ABC is a triangle with ∠B = 90 , BC = 3 cm and AB = 4 cm. D is point on AC such that AD = 1 cm and E is the midpoint of AB. Join D and E and extend DE to meet CB at F. Find BF.

Solution

Consider DABC . Then D, E and F are respective points on the sides CA, AB and BC. By construction D, E, F are collinear. 

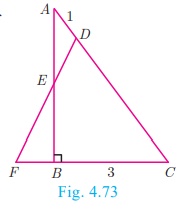
By Menelaus’ theorem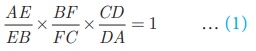 

By assumption, AE = EB = 2, DA = 1 and

FC = FB + BC = BF + 3

By Pythagoras theorem, AC ²  = AB² + BC ² = 16 + 9 = 25. Therefore AC = 5

and So,  CD = AC – AD = 5 – 1 = 4.

Substituting the values of FC, AE, EB, DA, CD in (1),

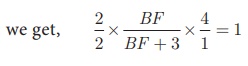
4BF = BF + 3

4BF – BF = 3 therefore BF = 1

Example 4.34

Suppose AB, AC and BC have lengths 13, 14 and AFFB 15 respectively. If AF/FB = 2/5 and CE/EA = 5/8. Find BD and DC.

Solution

Given that AB = 13 , AC = 14 and BC = 15.

Let BD = x and DC = y

Using Ceva’s theorem, we have,  

BC = BD + DC = 15 so, x + y = 15 

From (2), using x = 4y in (3) we get, 4y + y = 15 gives 5y = 15 then y = 3

Substitute y = 3 in (3) we get, x = 12 . Hence BD = 12 , DC = 3.

Example 4.35

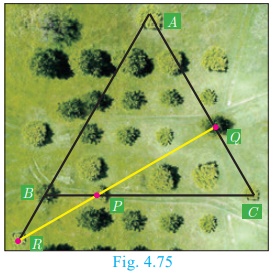
In a garden containing several trees, three particular trees P, Q, R are located in the following way, BP = 2 m, CQ = 3 m, RA = 10 m, PC = 6 m, QA = 5 m, RB = 2 m, where A, B, C are points such that P lies on BC, Q lies on AC and R lies on AB. Check whether the trees P, Q, R lie on a same straight line.

Solution

By Meanlau’s theorem, the trees P, Q, R will be collinear (lie on same straight line)

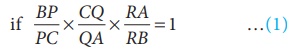
Given BP =2 m, CQ =3 m, RA =10 m, PC =6 m,

QA = 5 m and RB = 2 m

Substituting these values in (1) we get, BP/PC × CQ/QA × RA/RB = 2/6 × 3/5 × 10/2 = 60/60 = 1

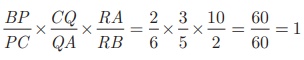
Hence the trees P, Q, R lie on a same straight line.

Progress Check

1. A straight line that touches a circle at a common point is called a _______.

2. A chord is a subsection of _______.

3. The lengths of the two tangents drawn from _______ point to a circle are equal.

4. No tangent can be drawn from _______ of the circle.

5. _______ is a cevian that divides the angle, into two equal halves.